受験生の皆さん、こんにちは。
東大合格ビジネスマンのワタシですm(_ _)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ ３大基礎力重視の裏ワザ勉強法
について、様々な情報を発信しております📢
2021年入試、旧帝大の第３弾は
「九州大学」です。
当ブログの解説記事は
読者が必死に３年間努力すれば
東大(理三以外)・京大(医以外)・九大医
レベルに80％以上の確率で合格できる
ことを目的に作成しています
市販の問題集のように、解法を丁寧に示すだけではありません！多角的なアプローチで問題を解きほぐしています✊
① 各問の難易度
② 他分野や一般常識との関連事項
③ 問題の躓きポイント
④ 極力曖昧な表現をしない説明
を示しています。
イマイチ成績が突き抜けられない受験生に貴重な情報が提供できればと思いますm(__)m
九大理系数学の特徴
九州大学の理系数学は全５問で制限時間は150分です。６問設定の大学より時間的余裕はあるけど、計算処理がやや重めの印象です。例年、第５問が難問化する傾向があります。
深く理解するには
全統記述模試で偏差値55~60
程度は欲しいですね🧐
全統記述模試の難易度や受験者レベルについては、各自で確認されてくださいm(__)m
第１問
【解答】
(１) 標準
＜答１＞ ベクトルの利用
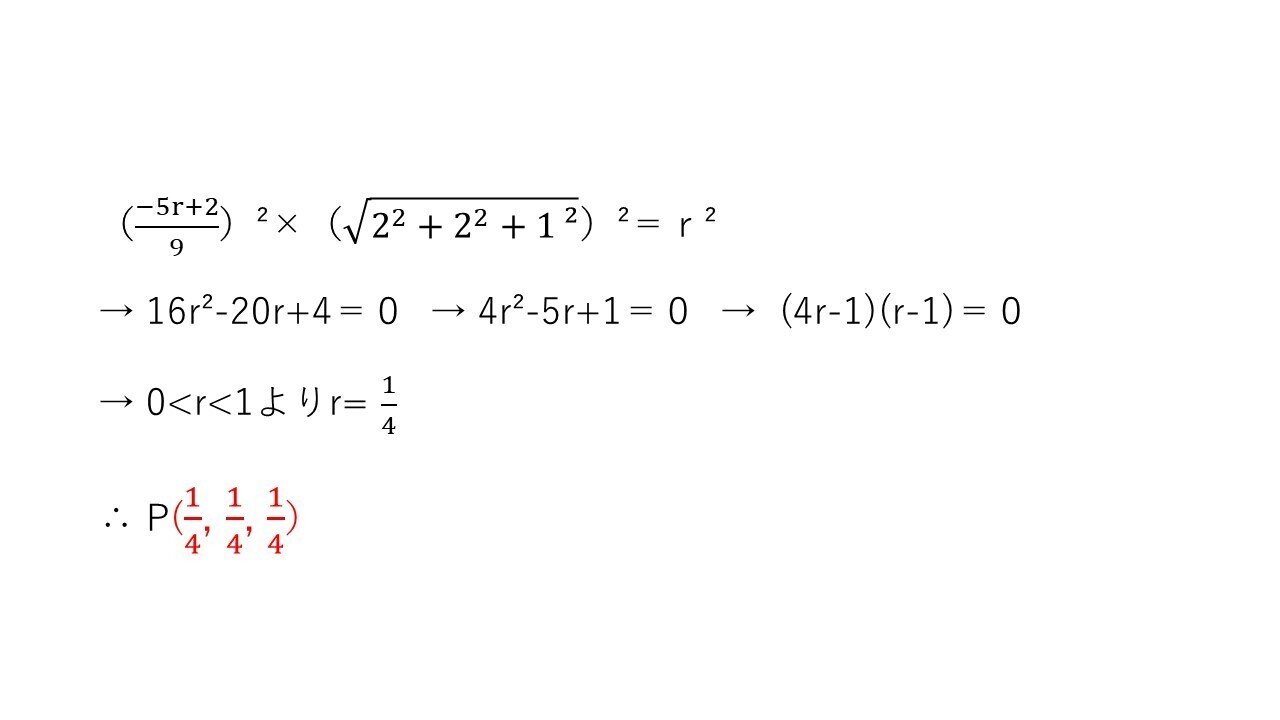
＜答２＞ 四面体OABCの体積の利用
＜分析＞
(1)にしてはやや重めかな～。
解法自体は典型的なのですが
最後にPH=rの条件を自分で用意する必要があったので、簡単とは言い切れない
難易度です。
＜答２＞では、△ABCに対してベクトルの面積公式(👇)を用いました！
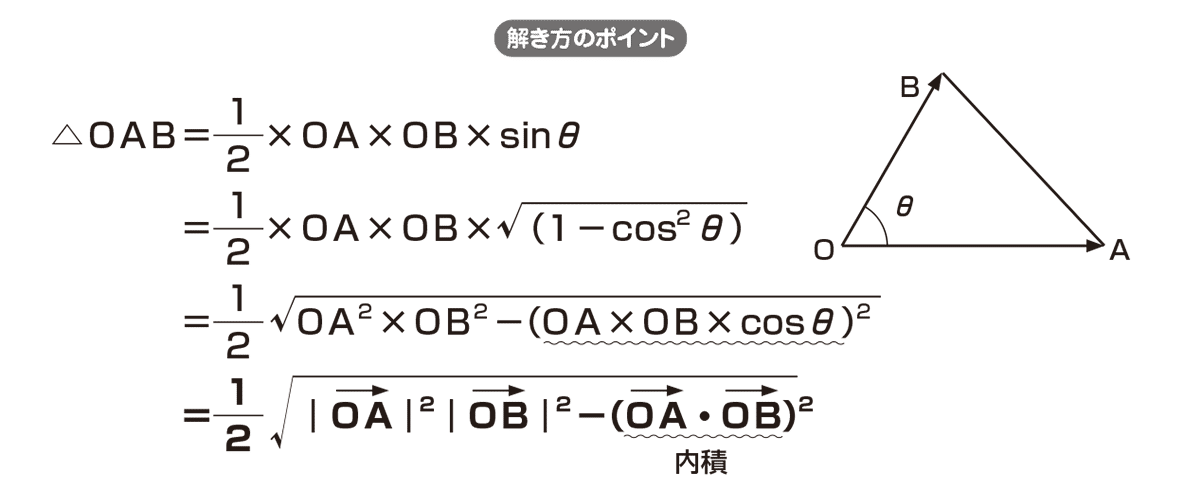
(２) 標準～やや難
＜分析＞
(1)を＜答２＞で解いてしまった受験生は詰まっただろう、ある意味嫌らしい問題ですね🤥
＜答１＞で解いた場合はQHの長さは出ますが、不注意で絶対値を付け忘れた受験生がそれなりにいたと思われます。すると、Rの範囲を誤り最終結果も誤るという災難に見舞われます😱
＜感想＞
最初からベクトルを使えば一直線ですが、(1)は幾何でもできてしまうため、幾何に固執すると(2)を落とす点で厄介です。
ベクトル計算はやや煩雑でしたね。う～ん、九大らしい😅
第２問
【解答】
(１) 易
(２) やや易～標準
(1)はできないと旧帝大志望として恥ずかしいでしょう。
判別式と２倍角の公式、どちらも超基本事項ですね。
＜分析＞
２次(３次)方程式が虚数解をもつときに、「実数係数より互いに共役な複素数解」の性質はよく使います！意外と忘れがち。
この手の問題は全統記述や駿台全国でも
お馴染みな典型問題
なので、よく身に付けておきましょう🙄
2021年の京大実戦でも出てました。
(３) やや易～標準
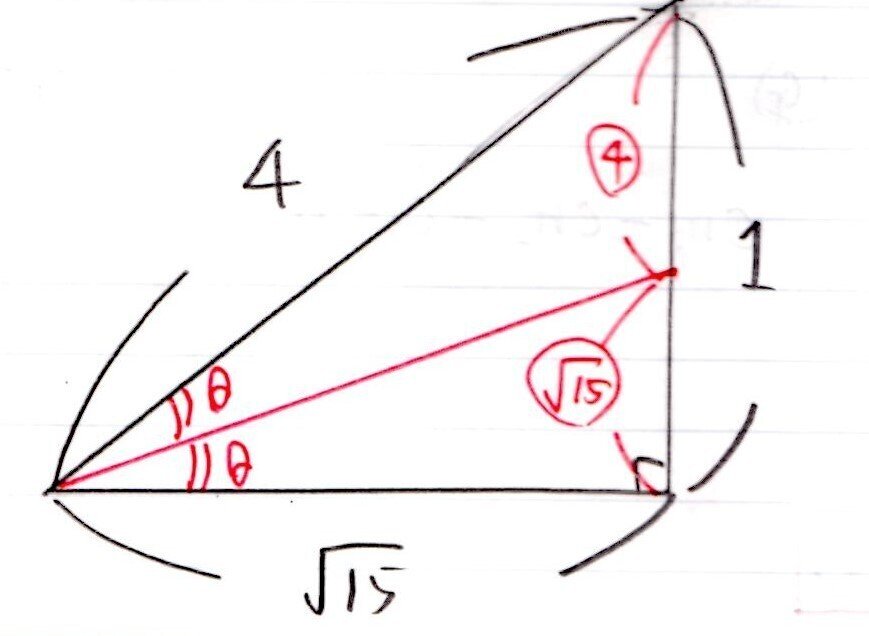
＜分析＞
(3)は角の二等分線の定理を覚えていたかがkey🔑
センター試験の数学ⅠA(幾何)では頻出事項でした！
第３問
【解答】
(１) 標準
＜分析＞
条件(＊)の「すべての実数tに対して」「(x,y)の集合を座標平面に表す」という表現から、tを変数にしてどんな操作をすべきか当たりをつけたいところですね～😎
「すべての実数tに対して⇒ tを変数と考える」の解法は、変数が２個以上出てきたときに有効なので、身に付けておきましょう✊
(２) やや難
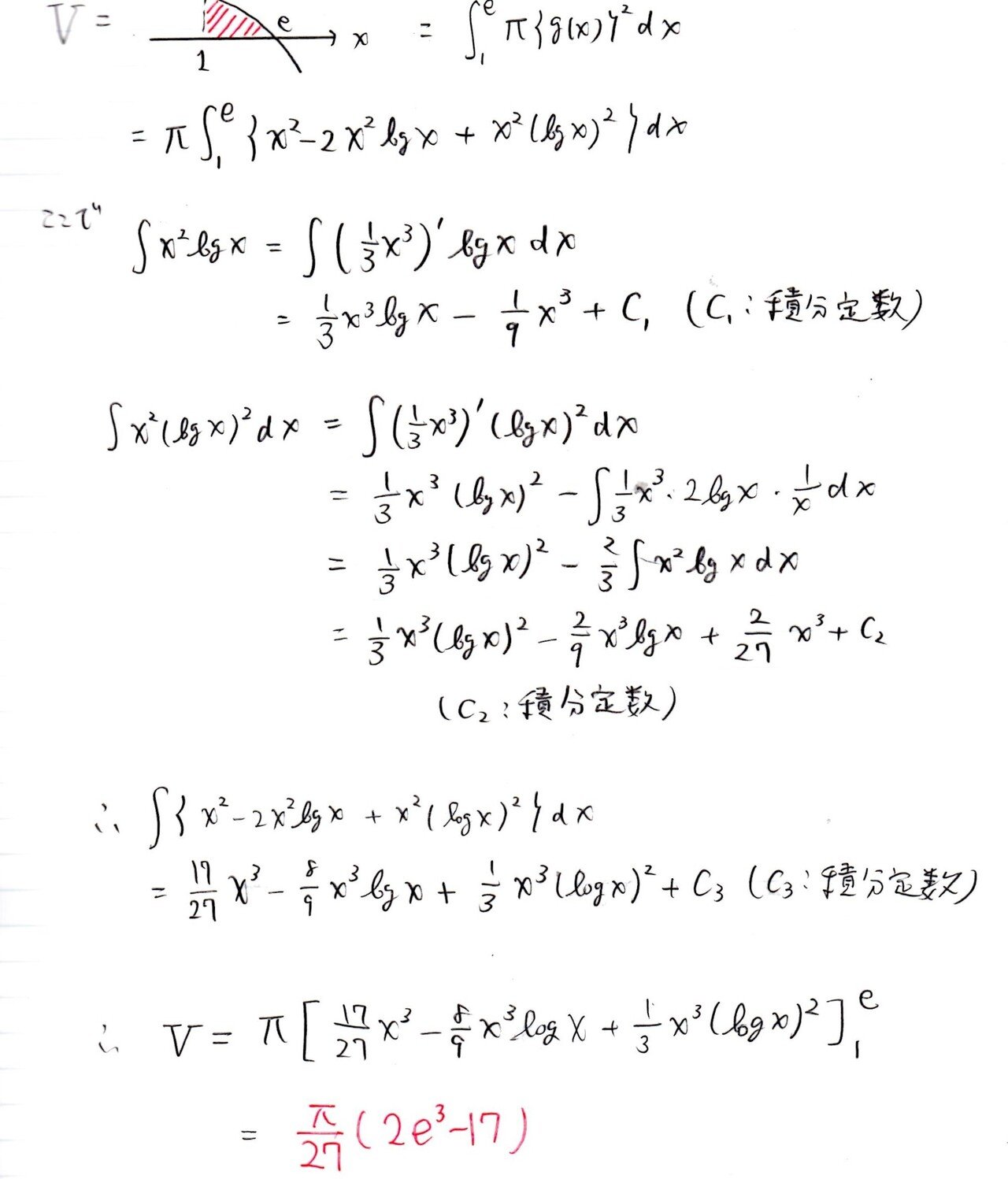
＜分析＞
(1)ができているのが前提ですね。
体積計算はなかなか激しい。しかも、答も綺麗じゃないし。これは計算ミスのリスクが高そう💦「∫(積分)にlogが絡む場合は、(logx)’=1/xを用いて部分積分」が鉄則です✊
第４問
【解答】
(１) やや易
＜分析＞
n=2なので、直接計算で行けると判断します🚩
与式にあるf'(x)とf(β)-f(α)/β-αを実際に計算し比較してみましょう。そうすれば、f'(x)のxにα+β/2を代入すればよいことがわかるでしょう👀
(２) 標準～やや難
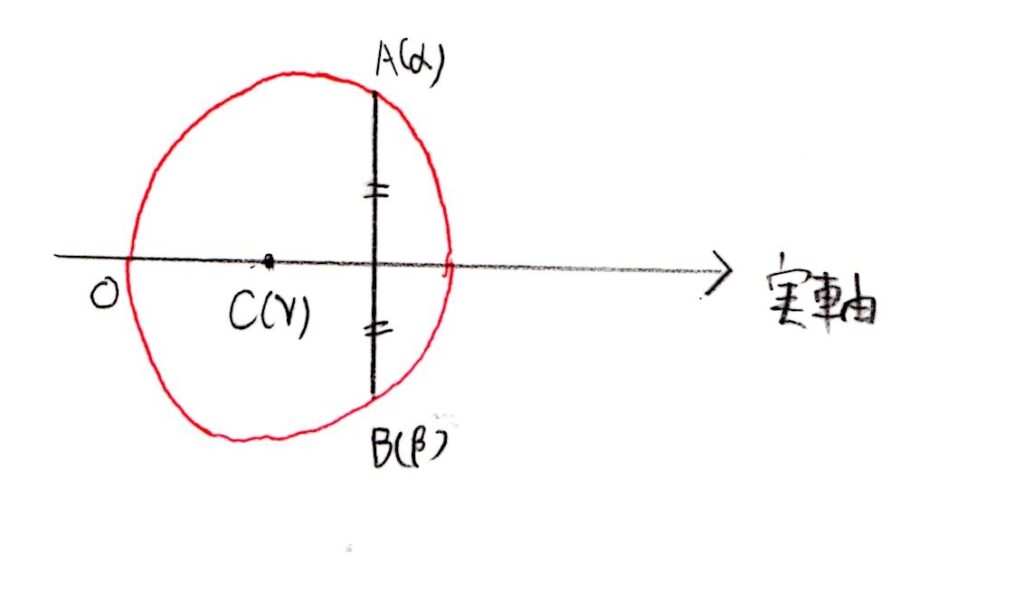
＜分析＞
α,βが与えられていることより、γ＝1+tiとおけます。-1≦t≦1のすべてのtに対してf'(γ)＝０が成り立つようなa,b,cの条件を求めればいいです。
計算地獄を覚悟で、直接計算に踏み切れたかが分かれ目でしたね。
「(実部)＝０ かつ (虚部)＝０」に着目するのがポイントです。これは、a+b√2＝0でa=0,b=0をいうのと同様の考え方です。
(３) やや難
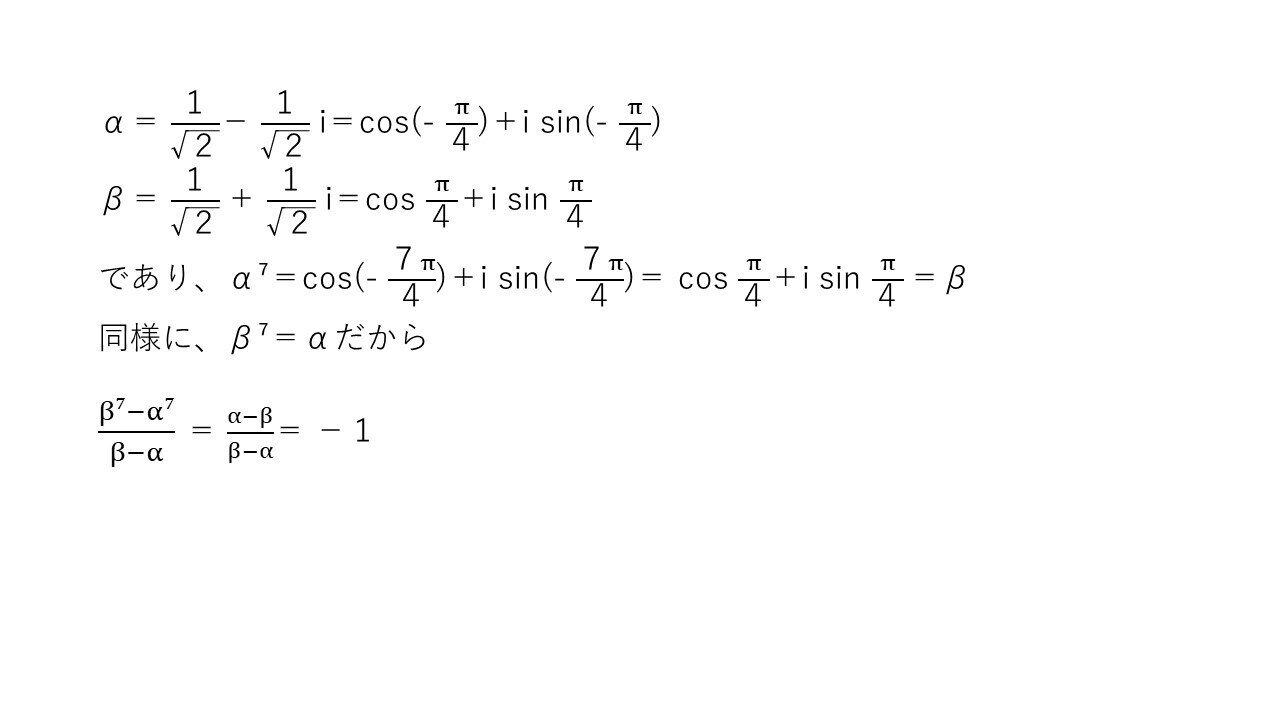
＜分析＞
７乗がデカくて直接計算が困難なこと、α,βが|α|=1,|β|=1で、かつ有名角を用いた極形式で表されることに着目するのがポイントでした。
α⁷はド・モアブルの定理を利用すれば楽勝ですね！！
また、「～でないことを示す→背理法(または対偶)の利用」はお馴染みのパターンなので、直接証明に困ったときの解法としてストックしておきましょう✊
＜感想＞
平均値の定理の複素数バージョンの登場です(笑)。シグマが絡む見た目ごつい問題ですが、とにかく一度手をつけてみましょう！
実際に難しいかどうかは手をつけてみないとわかりませんから💦
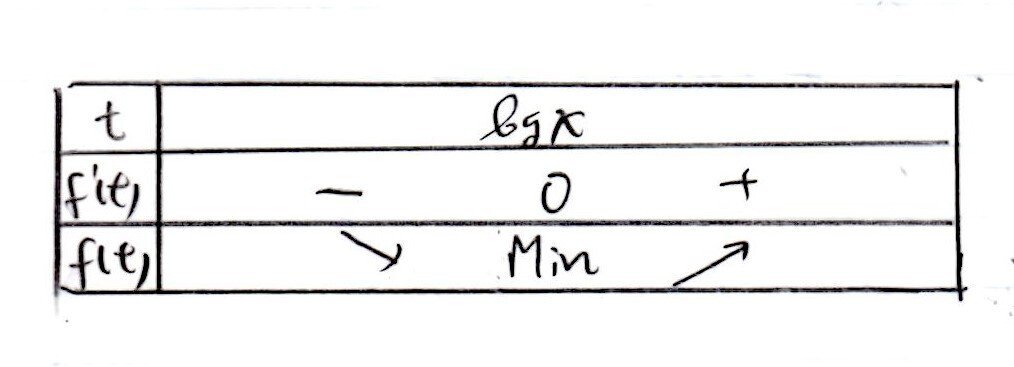
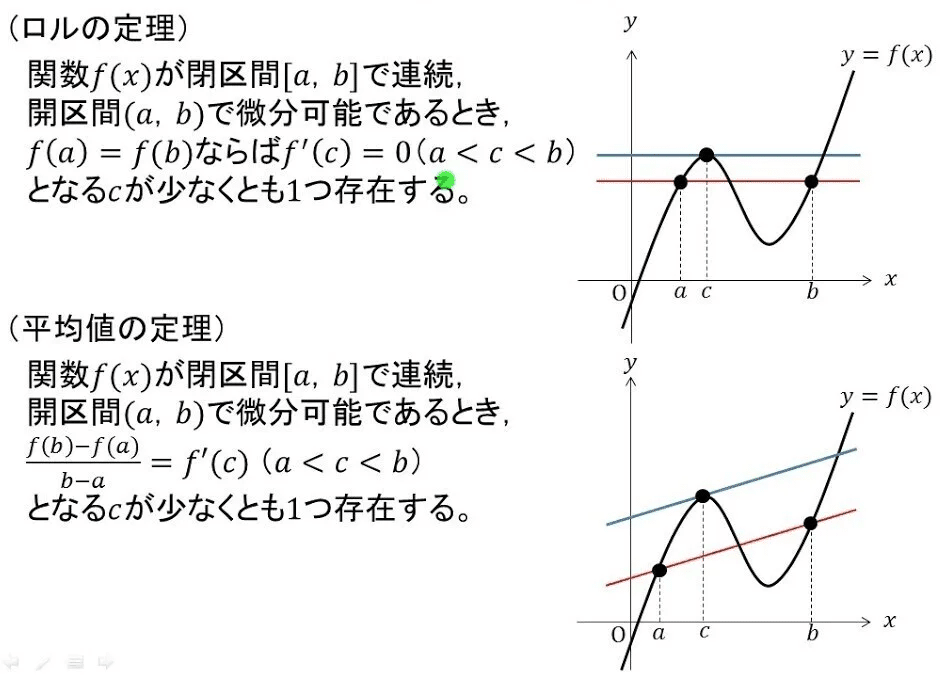
(平均値の定理)
一応おさらい的に示しますと・・・「ロルの定理」「平均値の定理」とはこんな定理でした👀
第５問
【解答】
(１) やや易～標準
＜分析＞
nC₁＝ｎであり、nCkがk=n/2に近付くにつれて大きくなることから、不等式の成立は何となく自明でしょう。
(２) 標準
＜分析＞
(n,k)の組合せを求める問題ですが、求める組はどうせ多くないのだろうと勘が働くと思うので、条件を絞ってやるとよいですね👆
「pＣkがpの倍数」の問題経験があればすぐにn=pか？と推測がつくけど、経験がないと手こずったでしょう。上の解答もn=p以外は不適なんだろうと見越して作成したもの。
特に、「pＣkがpの倍数であることを示せ」は2009年東大理系数学第１問に出題されています(解答は省略)👇
総括
取りやすい問題は、第１問(1)、第２問、第４問(1)、第５問(1)くらいで、後はどれも一山あります。
特に点差が開くのは第３問でしょうか。
(2)の体積計算も煩雑ですが、(1)で「すべての実数tに対して」を正しく解釈できたかでall or nothingになりうる問題だと思います😨
今回の難易度だと
非医：50~55％
医：70～75％
が合格点でしょうか🤔
医志望は、第２問と他２問を完答して、第３問の０点を回避するのが理想的な取り方でしょう。
