
受験生の皆さん、こんにちは。
東大合格ビジネスマンのワタシですm(_ _)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ 3大基礎力重視の裏ワザ勉強法
に関する様々な情報を発信しております📢
私の公式LINEでは、無料相談を随時受け付けております。
公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってください✊
私も苦手科目は先生に頼りました。
また、LINE登録していただいた方には
無料プレゼント(1年で偏差値70出す画期的勉強法)
を贈呈します🎁
【⬇️公式LINE登録はこちら⬇️】

2021年入試、旧帝大の第6弾は
「京都大学」です。
当ブログの解説記事は
読者が必死に3年間努力すれば
東大(理三以外)・京大(医以外)・九大医
レベルに80%以上の確率で合格できる
ことを目的に作成しています
市販の問題集のように、解法を丁寧に示すだけではありません!多角的なアプローチで問題を解きほぐしています✊
① 各問の難易度
② 他分野や一般常識との関連事項
③ 問題の躓きポイント
④ 極力曖昧な表現をしない説明
を示しています。
イマイチ成績が突き抜けられない受験生に貴重な情報が提供できればと思いますm(__)m
京大理系数学の特徴
京大の理系数学は150分で全6問です。
原則として、誘導はなくall or nothingな出来に分かれることが多く、非常に得点差がつきやすい構成となっています。
2000年頃の問題よりは確実に易化しており、京大受験生基準で、やや易2〜3問,標準2〜3問、やや難1〜2問の状態で落ち着いています。
ただ、ここで歓喜すること勿れ。
つまり
数学苦手が
ますます合格しにくい
仕様になっている
ことを示唆しています🥲
第1問

【解答】
(1) 易~やや易


<分析>
超頻出のベクトルの垂直条件の問題です。「点Mが平面ABC上にあること」「PQ⊥(平面ABC)」に着目し、ベクトルを空間座標で表して内積計算をすれば、答が出ます。
(2) やや易

<分析>
(n-1)回目までに赤以外の3色すべてが出る場合の数を求めるのがキモです。
ここは、1色のみ、2色のみの場合を求め、余事象的に考えるとすんなり答が出ます。
<感想>
今年の第1問は別個の問題2つで40点配点。2018年以前ではみられない配点で来ましたか。ついでに、第6問も40点配点となってます。
問1はベクトル、問2は確率。
両者とも全統記述模試問題で出てもおかしくないレベルなので、京大合格を目指す受験生なら取りたいですね👌
第2問

難易度:やや易~標準
【解答】


<分析>
第2問は平面座標の問題です。これも非常によくあるタイプですね。京大受験層を意識して言うと、さすがに点Qは出せるでしょう。
L²はtの商の形ですが、平方完成や相加相乗ではうまくいかなさそうですね。
平方完成や相加相乗平均の関係では難しい場合は、迷わず微分で進めてみるのがポイントです!
第3問

難易度:やや難
【解答】
① 周期6ごとに分けて計算する

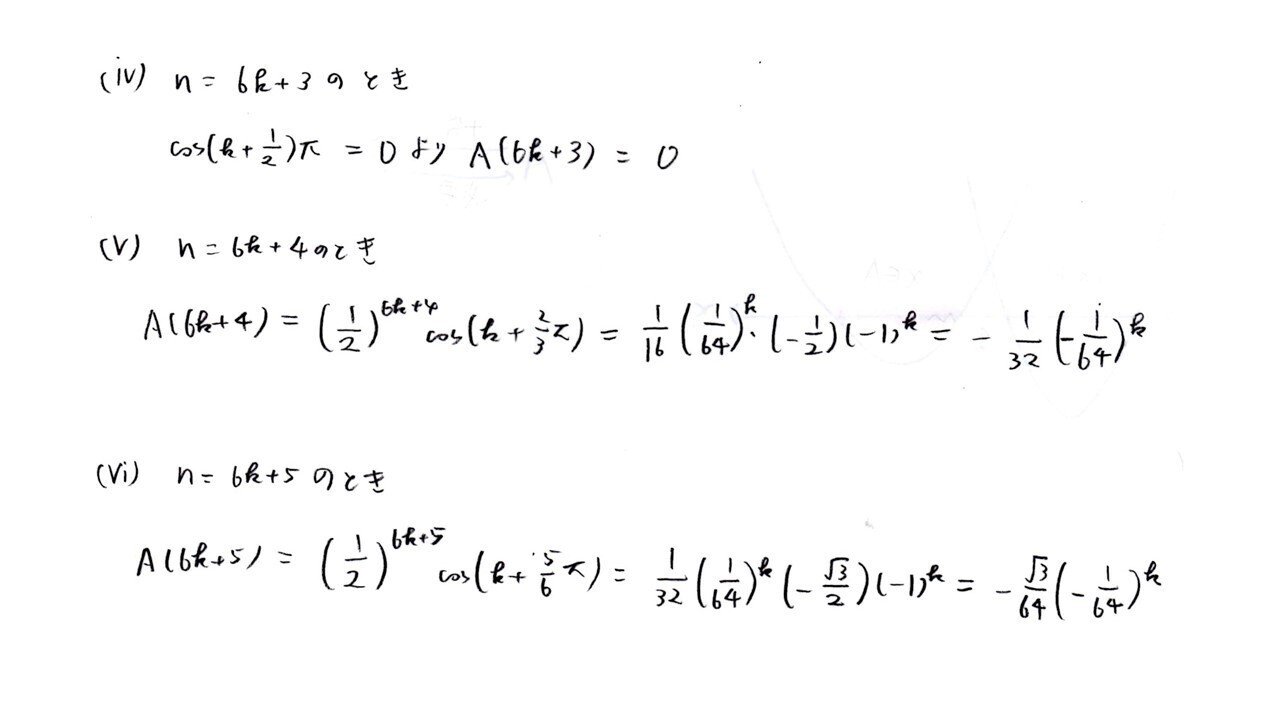
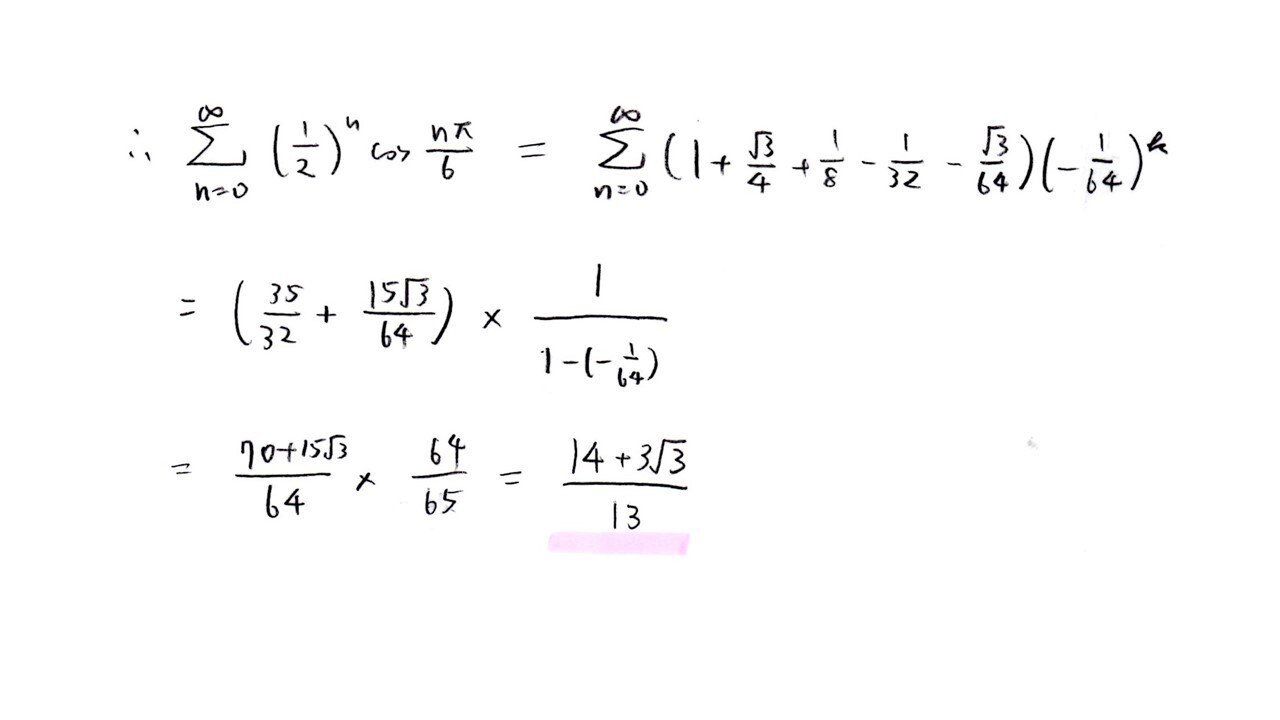
② n乗と三角関数絡み
⇒ (与式)を複素数の実部とみなす
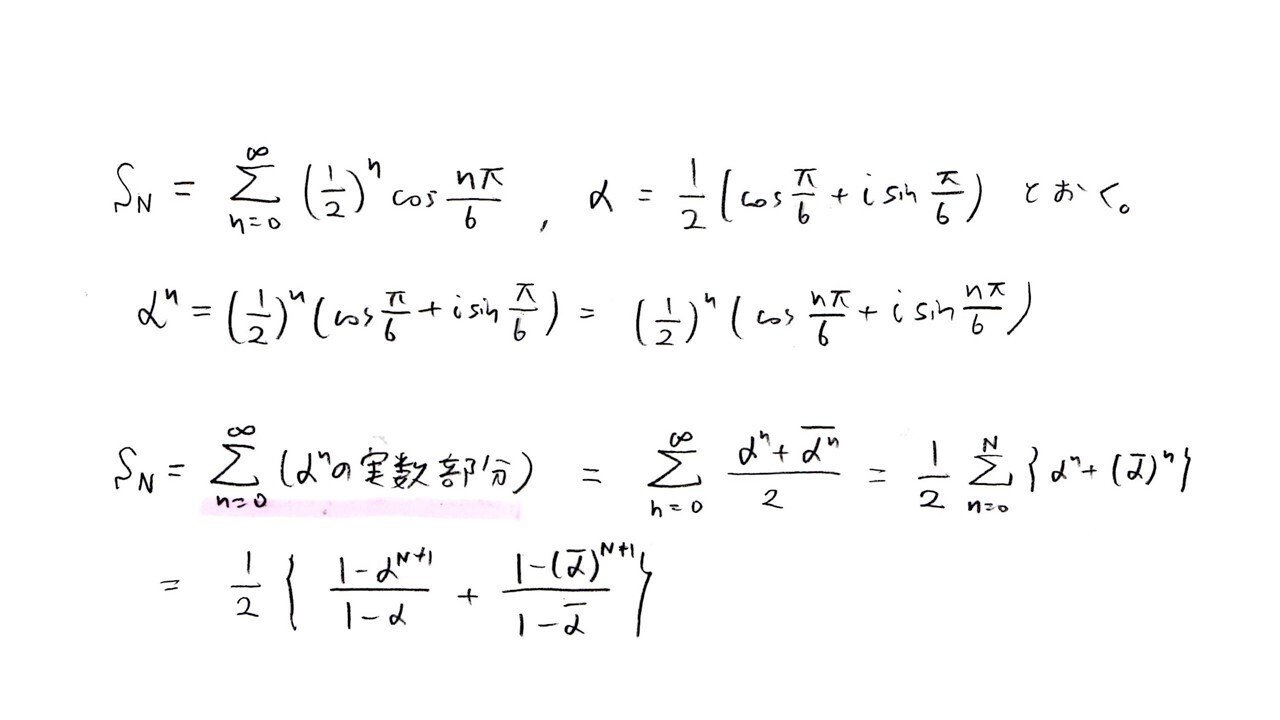

<分析>
三角関数の絡むΣ問題は、とりあえず周期をみつけてゴリ押し計算すれば答は出ることが多いです。
今回も①のようにゴリ押したら、時間は食うけどちゃんと出ました💡
②では、「αⁿの実部の和を数式化する部分」「|α|の極限を示すことでlimαⁿ→0をいう部分」が経験がないと難しいですね。複素数も数列風に扱えるというのが。ただ、今後、複素数を用いて求める手法もスキルの1つとして身に付けるとよいでしょう。
第4問
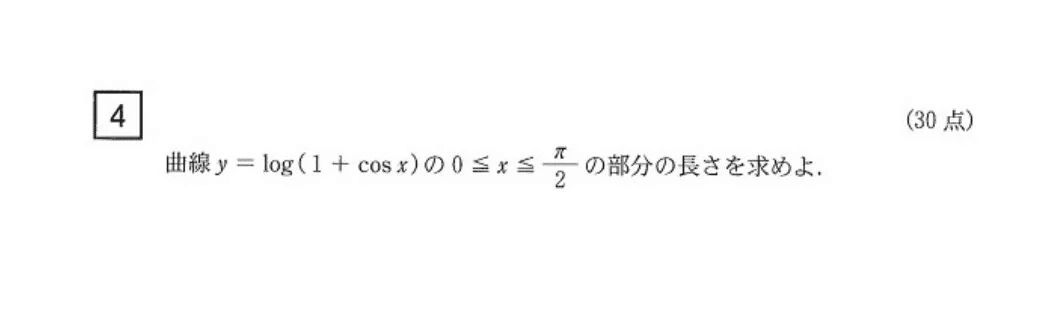
難易度:やや易~標準
【解答】
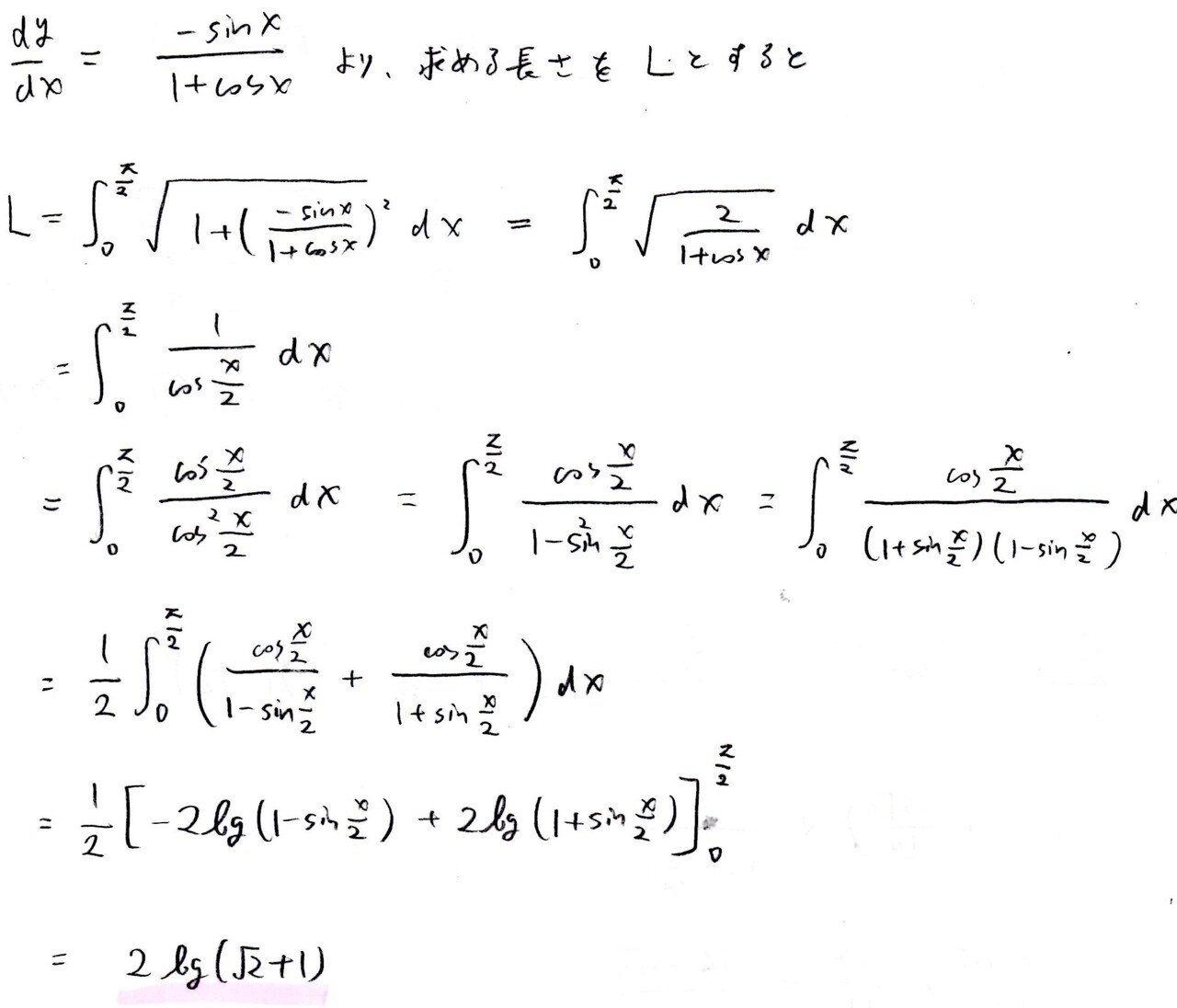
<分析>
曲線の長さですか・・・数Ⅲの積分の最後の方に出てくるやつですね。
∫内にsin,cosの一方がある場合、sinとcosを共存させるような変形をすると解けることが多いですね。∫1/cosx dx系の積分はマトモな京大受験生なら経験はあるはず。
しかし曲線の長さの公式を
覚えていたかどうかが全て!
みたいなall or nothing的な問題
でしたね。
これは合否を分けた1題でしょう😅
曲線の長さは、導出過程も理解しておくのが理想の形ですが、今回みたく覚えてれば満点が取れる分野なので最悪、覚えることが最優先です💪
【曲線の長さL】
第1式はy=f(x)のx,y媒介変数θで表されるとき、第2式はy=f(x)で表されるときに用いる公式です。
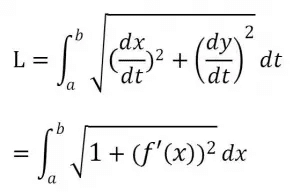
第5問

【解答】
(1) やや易
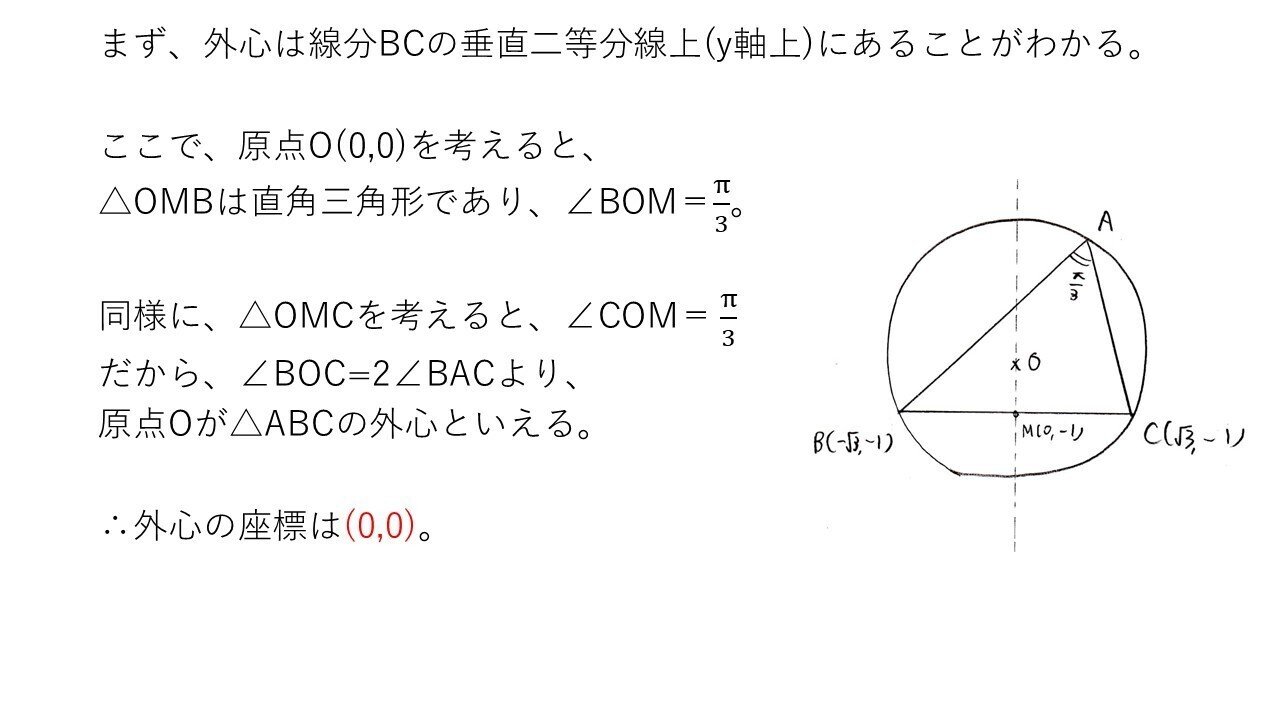
<分析>
中学幾何の問題(笑)
簡単なんですが、中学数学の内容を意外と忘れている受験生もいたのでは?今回は「円周角と中心角の関係」を使いましたが、「接弦定理の逆」なんかも忘れた頃に出るかもよ🙄
(2) 標準


<分析>
まず、外心と垂心の意味が曖昧だった人は言葉の復習から。
(2)は点Aから直線BC(=x軸)に下ろした垂線上に垂心があることに着目して、Aのx座標と垂心のx座標が一致することを見出すとよかったですね。あとは、H’の座標(x,y)を設定してベクトルの内積=0に持ち込めば解けます。
第6問

【解答】
(問1) 標準~やや難

<分析>
(問1)は知識・経験で差が付いた気がします。発想面でレベルが高い。
入試数学では「直接証明が難しいなら背理法と対偶!」を意識です💡
実は、私も京大オープンの過去問で経験していたからこの発想ができただけです。
(問2) やや難~難


<分析>
f(a)=af'(1)の形を見て商の微分を思い付けたかどうかが勝負でした。
さらに、平均値の定理を利用します。どちらも「言われれば確かにそうだよな」とは思うけど、自分で気づくのは結構難しいんですよね😱
<感想>
問1,2とも難しめなので、非医志望なら最悪0点でも仕方ないでしょう。
医志望なら(1)は何とか取りたいところ。
総括
今年は、難易度差があったセットだと思います。
第1問、第2問、第4問、第5問(1)は簡単なので、確保したいところです💪
あとは、垂心をきちんと理解していれば第5問(2)は取れる、周期に気付いてゴリ押しすれば第3問も取れるといった状況でしょうか。
第6問は最難問なので、非医なら全滅でも仕方ないか😵
ボーダーは
非医:50~55%
医:70~75%
程度でしょう。
医志望なら第6問全滅は回避したいところですが、第1~5問までを完答できていればOKだと思います。
最後に、再度公式ラインの紹介をします。
私の公式LINEでは、無料相談を随時受け付けております。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってみてください✊
【⬇️公式LINE登録はこちら⬇️】



