
受験生の皆さん、こんにちは。
東大合格ビジネスマンのワタシですm(_ _)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ 3大基礎力重視の裏ワザ勉強法
また、私の公式ラインでは無料相談を随時受け付けております。
公立中学出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、いち受験のプロの私に相談してみてください✊
私も、できない科目は先生を頼りました。
また、LINE登録していただいた方には
無料プレゼント(1年で偏差値70出す画期的勉強法)
を贈呈します🎁
【⬇️公式LINE登録はこちら⬇️】

普段は共通テストや旧帝大理系入試をメインに解説記事を作成しておりますが、1校くらいは私大の解説記事もアップしようかと思いまして…
東大志望の滑り止めになりやすい「慶応理工」に絞って解説することにしました。
科目は
数学・物理・化学!
英語は旧帝大と傾向が違いすぎるため却下してます✋
では、早速問題を見ていきましょう👀
第1問

【解答】
(1)
(ⅰ) 易~やや易
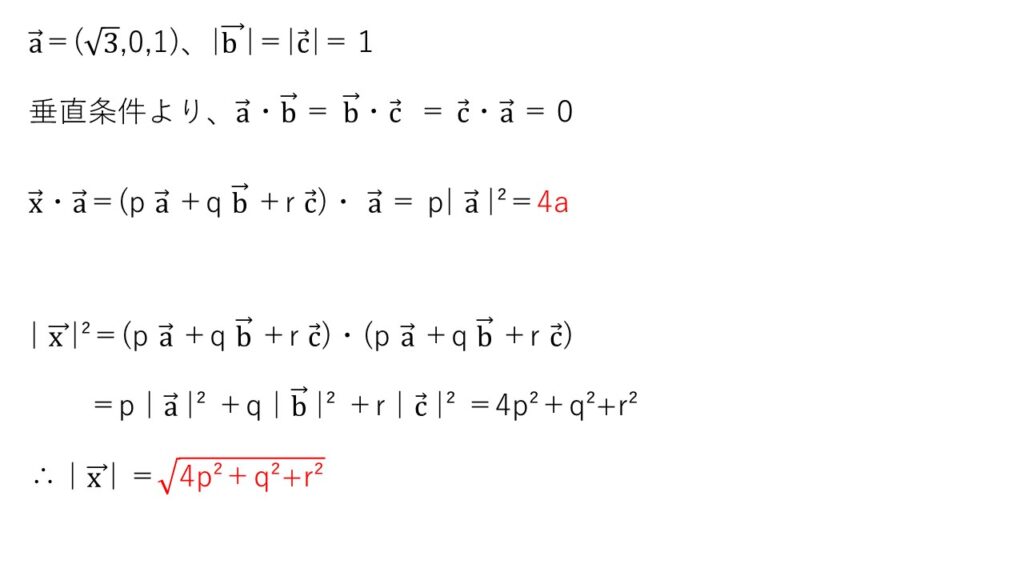
<分析>
ただの内積計算。
a,b,c各ベクトルの絶対値が2,1,1である点を読み取れれば本問は楽勝です!
(ⅱ) やや易~標準

<分析>
答を出すだけの問題。
(ア),(イ)を利用して2つの方程式を出し、sを消去すれば、zの値は出ます。θの存在を厳密に示す必要はない点では、結構楽ですね。
(2) やや易
<解答1>

<解答2>

<分析>
nは奇数なので、解答のようにn=2k+1(kは0以上の整数)とおくと話が早いです。
ガウス記号[]は難関大で頻出なので、説明なしでも使える状態にしておきたいですね💡
第2問

【解答】
(1) やや易~標準

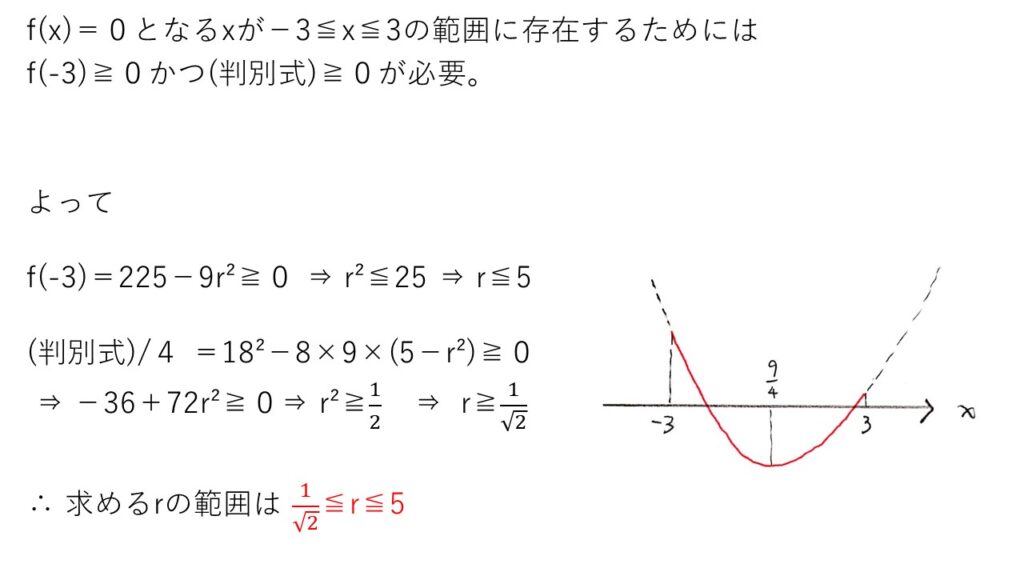
<分析>
本問は(判別式)≧0のみを求めて「あれ?おかしいぞ?」と混乱した受験生がまあまあいたと思います💦
実際に楕円を描くと-3≦x≦3なのは自明なのですが、数式処理すると何で間違えるのか??・・・間違えた方は自分でよく考えてみるのもアリですね。
ところで、円と直線の場合ではなぜxの範囲が必要ないのでしょうか🤔❓それは、例えば直線の式が3x+5y-1=0とするとき、yはxが実数全体を動くときにyも実数全体を動くからなんです。
(2) 易~やや易
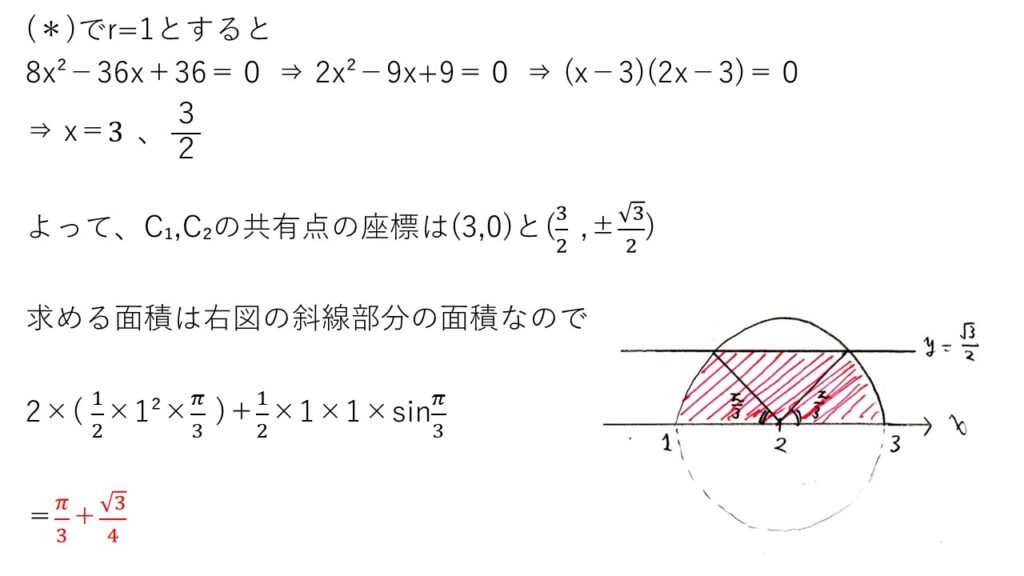
<分析>
(1)のrの範囲が出てなくても無関係にできる点でありがたいですね😂
求めるべき部分を示すのは容易でしょう。あとは、中学レベルの面積計算です。
(3) 標準
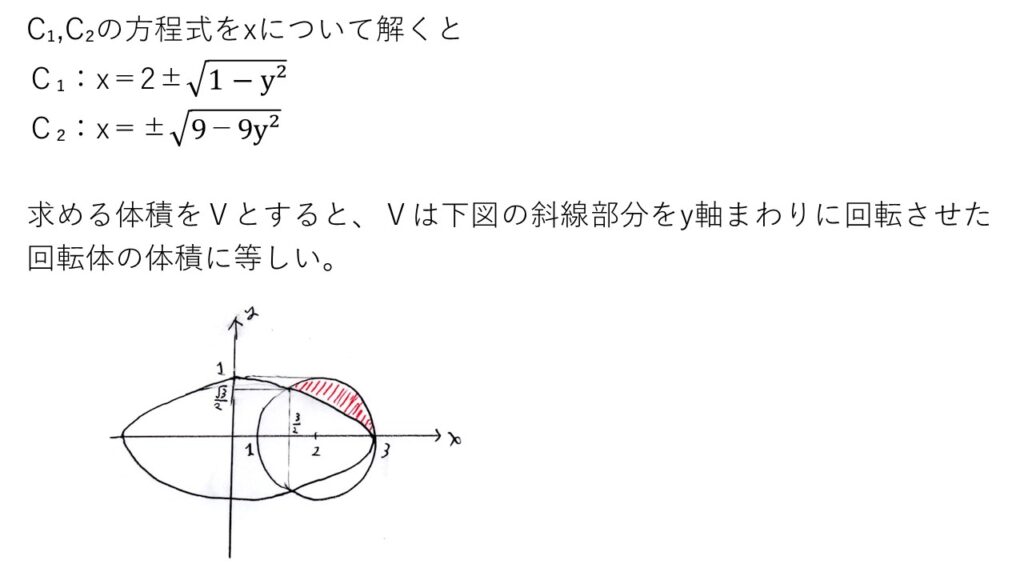
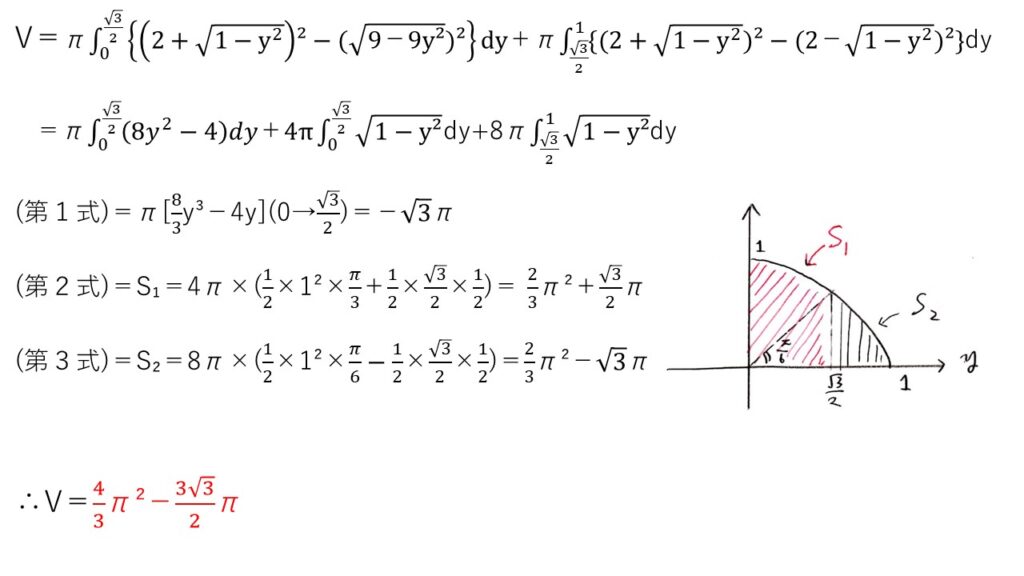
<分析>
名大が好きそうな問題だなあ🤔
実際に、名大模試でもこの類の問題はよく出ます。体積Vがなぜ上記のような式になるのか理解できますか?
具体的に文章で説明するのは難しいのですが、引く曲線の式は0≦y≦√3/2と√3/2≦y≦1で変わるのです💡
後半は、これまた中学レベルの面積計算ですね。
第3問

【解答】
(条件を図示)

(1) 易

<分析>
1回後の状態2通り(A,B)を書いてしまうとわかりやすいです。そして、A,Bについて次何を出せばよいか考えます。
(2) やや易~標準


<分析>
「白玉が出るとき、コインが必ず裏である」ことに着目しましょう👀
すると、裏が何回目に出るかで場合分けして考えればよいことがわかります。条件付き確率の定義はちゃんと理解していますか❓
(3) 易

<分析>
これは簡単。
背理法的に考察すると、ずっとコインの裏を出し続ける必要があるとわかります。
(4) やや易

<分析>
「1回目で赤を出す」と指定があるので、残り(k-1)回ですべて白を出せばよいとわかるでしょう☝
(5) やや易~標準

<分析>
(4)がヒントです。何回目で赤玉を出すかで考えるといいですね💡
ℓ回目に赤玉を取り出す確率(*)を求めたら、あとはℓ=1~kでシグマ計算です。
ちなみに、(*)では最後に白を出すことを前提で考えているので、ℓ=kのときは分けて考えないといけません。
第4問

【解答】
(1) やや易

<分析>
超典型問題ですが、注意点はa=0とa>0で分類することです。
なぜか?a=0ではf(x)が単調増加し、増減表を書いたときに極小値をもたなくなるからです。
(2)
(タ)(チ) やや易~標準
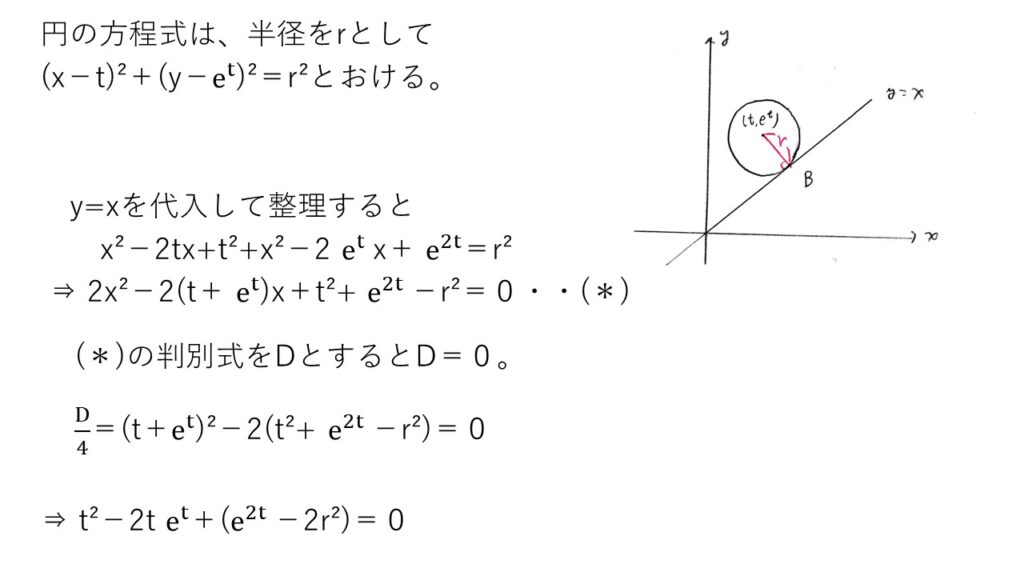
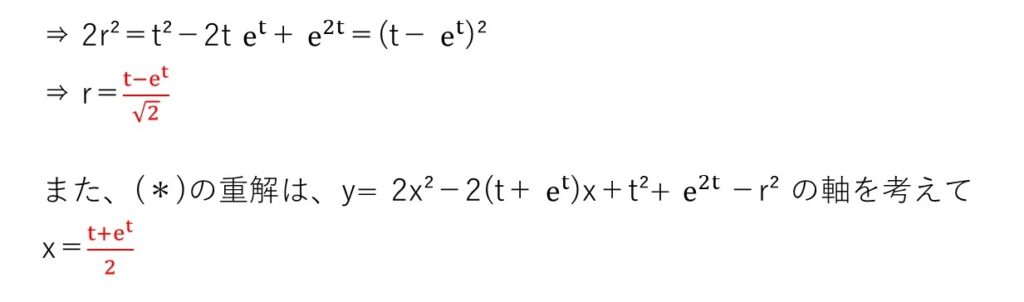
<分析>
円と直線の式を連立して2次方程式を導出します。そして、両者が接することからお決まりの(判別式)=0を使います。
(ツ) やや易~標準

<分析>
前問の正解が前提なので「やや易~標準」としました。
問題文にあるlim(x→∞) te−t=0に着目してte−tの形を作り出すことがポイントでしたね!!
式の途中で分母・分子にe⁻tを掛けているのがわかるでしょうか👀❓
第5問

【解答】
(1)
(テ) 易
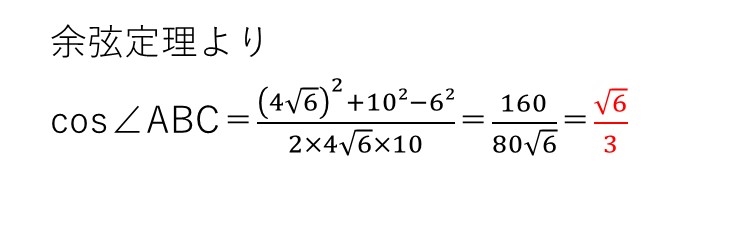
<分析>
3辺がわかっているのだから、余弦定理はミエミエでしょう👀
(ト) 易~やや易
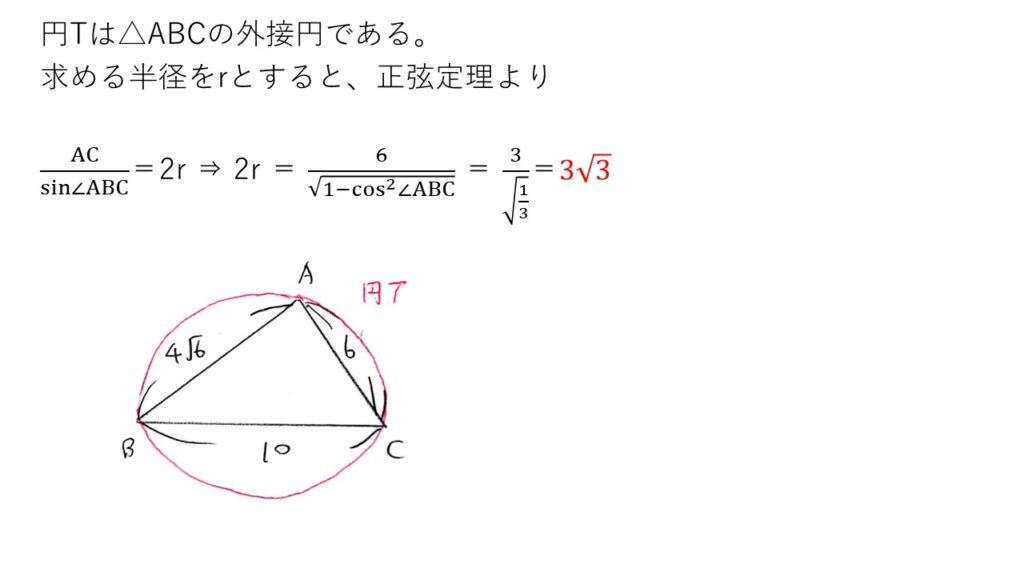
<分析>
3点A,B,Cは球S上にあり△ABCと同じ平面に円Tが存在するという条件から、円Tは△ABCの外接円です。
外接円の半径を求めるのだから、それに合った解法はやはり正弦定理でしょう。
(ナ) やや易

<分析>
ABを底辺として考えます。「点Dが弧AB上を動くときにどこで高さが最大になるか?」を考えると、△ABDが二等辺三角形のときですね💡
また、△ABDが二等辺三角形のときにDからABに下ろした垂線が円Tの中心を通る点に着目。
(2) 易~やや易

<分析>
円Tの外接円の半径が出れば楽勝。三平方の定理使うだけの問題・・・何をさせたかったのか(笑)?
(3) やや易~標準
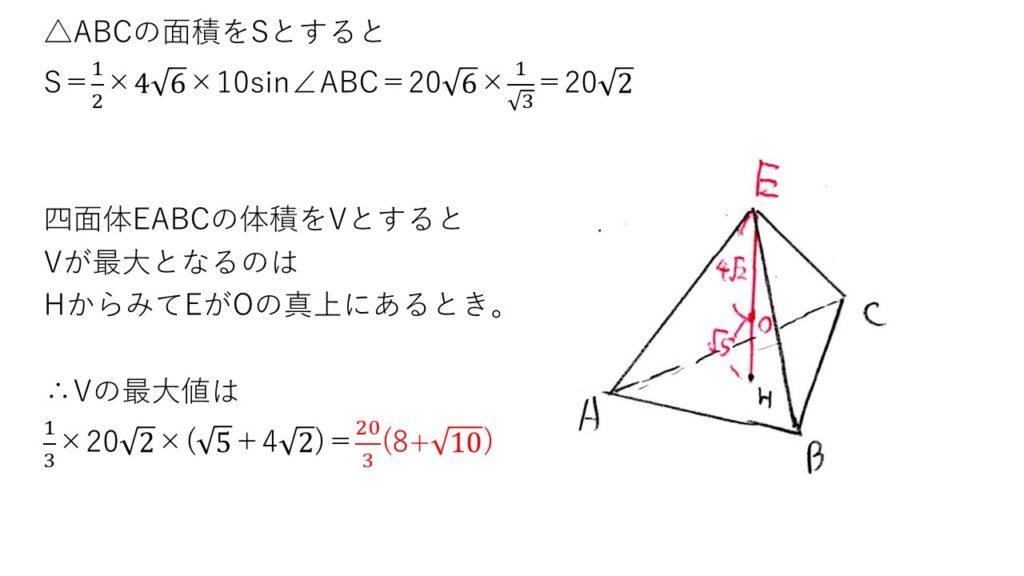
<分析>
(ナ)を応用します。
すると、Eが△ABCからみて球の中心(O)の直上であることは明らかでしょう。
あとは、△ABCの面積をsin∠ABCの値を用いて計算すればOKです。
総括
今年の慶応理工の数学はどうしちまったんだ!?
簡単すぎやしないか??

(https://www.ac-illust.com/main/search_result.php?word=これ何?より引用)
第1問は(1)(ⅱ)以外は取る、第2問は、第4問は多少計算処理の面倒さはあれど取れる、第5問は完答割と余裕。
東大理系志望なら80~85%は欲しいレベルですね~💡
最後に、再度公式ラインの紹介をします。
私の公式LINEでは、無料相談を随時受け付けております。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってみてください✊
【⬇️公式LINE登録はこちら⬇️】






