受験生の皆さん、こんにちは！
東大合格ビジネスマンのワタシですm(_ _)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ 3大基礎力重視の裏ワザ勉強法
について、様々な観点から発信しております！
今回は、2022年の共通テスト数学ⅡBを徹底解説していきます✊
私自身が現役プレイヤーなので、学校の先生や予備校講師といった指導者目線ではない、プレイヤー目線でまた違う徹底的に語りつくすことができるのでは？
と思い作成しましたm(__)m
ただ・・私、確率分布は未修でわからんのです。
ごめんなさいm(__)m
今回は理系科目難化と噂されていますが、難易度では凶悪で名高い数ⅠAよりは全然マシかな。
むしろ、問題量と完答のしにくさで潰しにかかってる感じでしょうか💦
では、早速問題を見ていきましょう！！
第１問
[１]
【解答】
（１）易
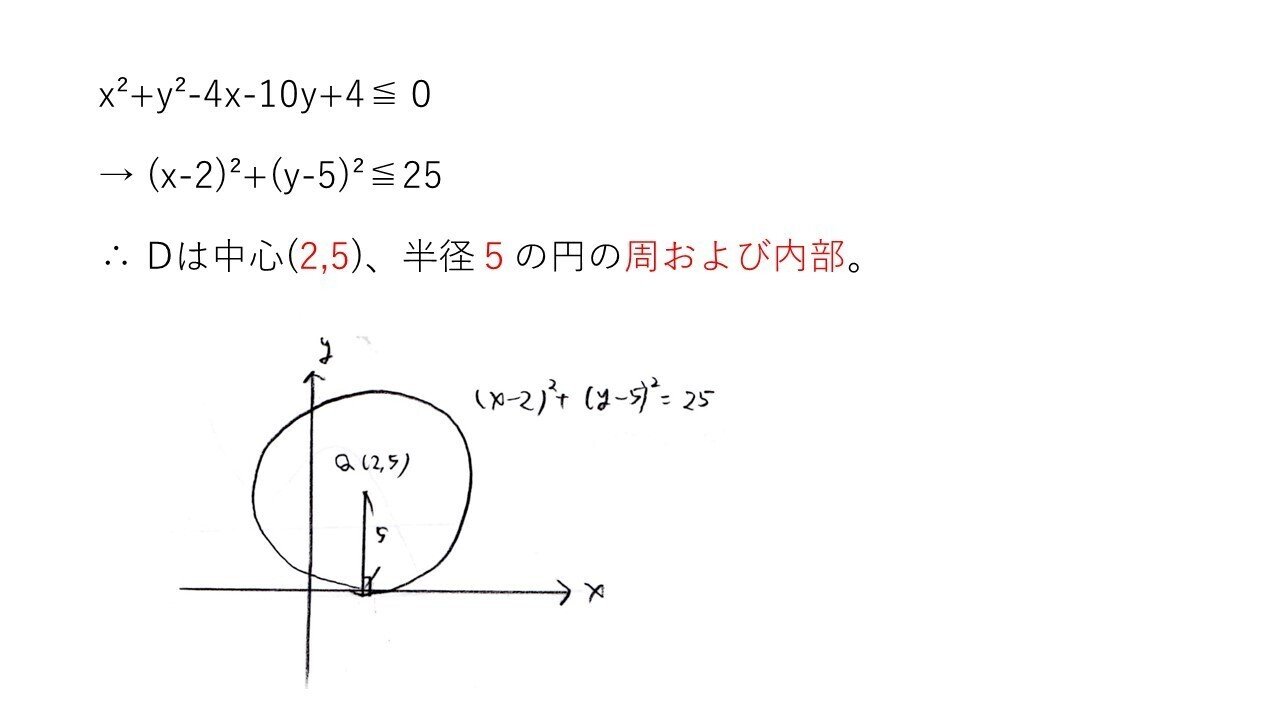
＜分析＞
ただ平方完成して円の式を作るだけです。(x-2)²+(y-5)²≦25は点(2,5)からの距離が√25＝５以下の部分全体を指します。
(２)
(ⅰ) 易
ｙ＝０
＜分析＞
実際に円を描くとx軸に接することがわかるので、y＝０はすぐわかります。
(ⅱ) 易
⓪ 重解をもつ
＜分析＞
円と直線が接するということは、両者の共通解はただ１つ・・・ということなので、判別式＝０が成り立ちます。
(ⅲ) 易～やや易
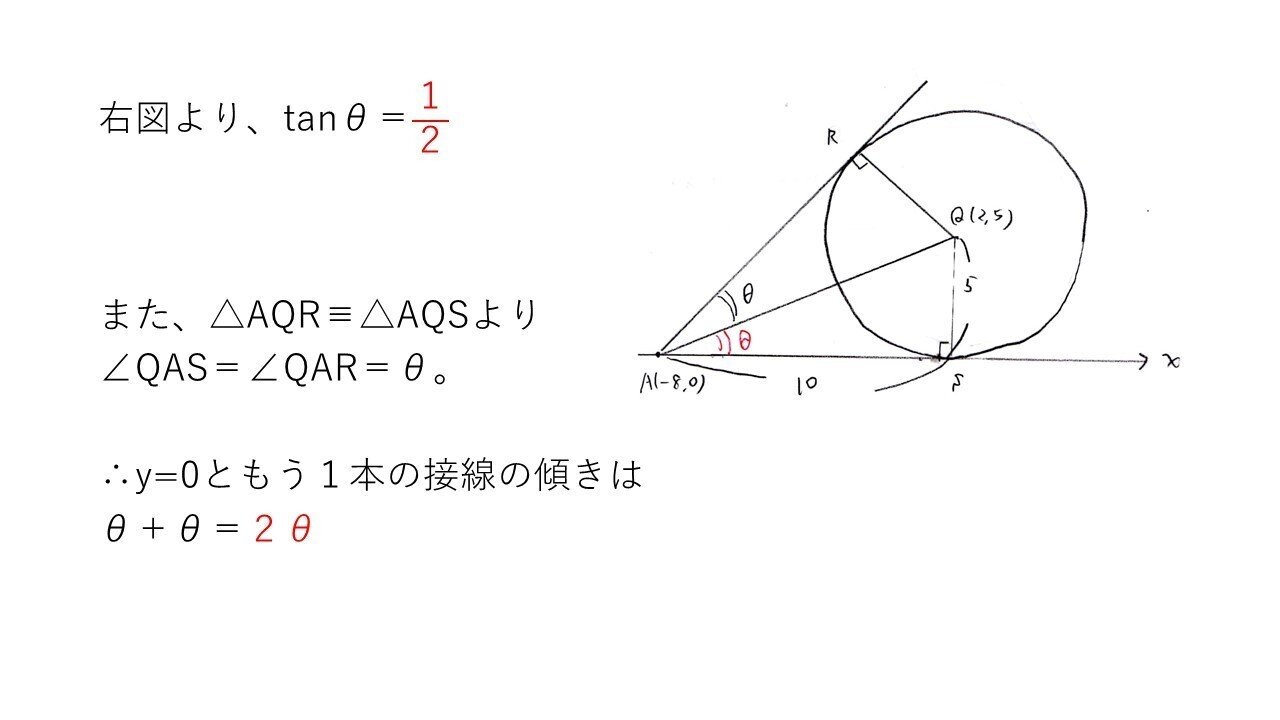
＜分析＞
tanθの値は楽勝でしょう！
y=0ともう１本の接線のなす角については、円外から２本接線を引いたときの性質(中学で習いましたよね？)に注目します👀
(ⅳ) やや易
＜分析＞
(判別式)＝０を解くでもtan２θを求めるでもいいけど、明らかに後者の方が計算は楽でしょう💦
ｋの範囲は図から明らかです。
[２]
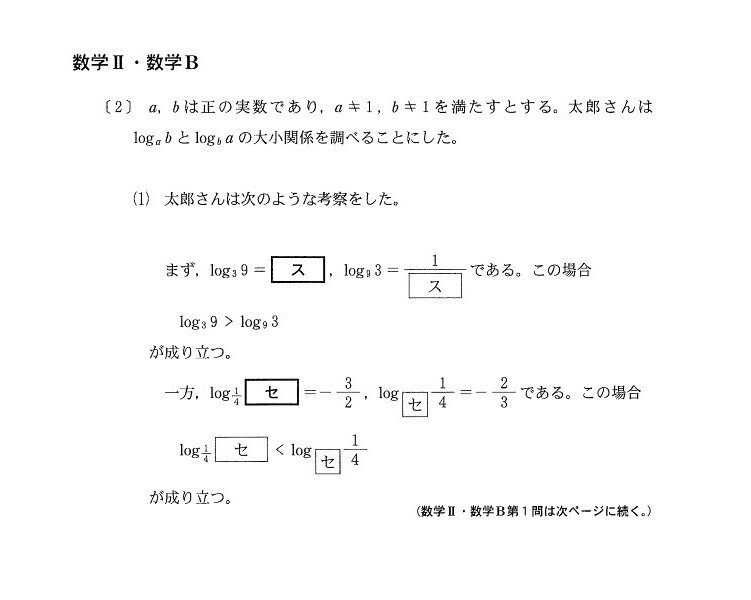
【解答】
(１) やや易
＜分析＞
後半は対数(log)の意味をきちんと理解できていない受験生は詰んだかも…答えるのは、1/4を－3/2乗した値ですよ～。
(２) やや易
(ソ)１、(タ) １
＜分析＞
これも対数(log)の意味が理解できていればできる問題。
(３) やや易～標準
(チ) ３ 、(ツ) ０
＜分析＞
面倒くさがらずにグラフを描けば見えてきます👀0<a<1とa>1でグラフの形は違いますよね。
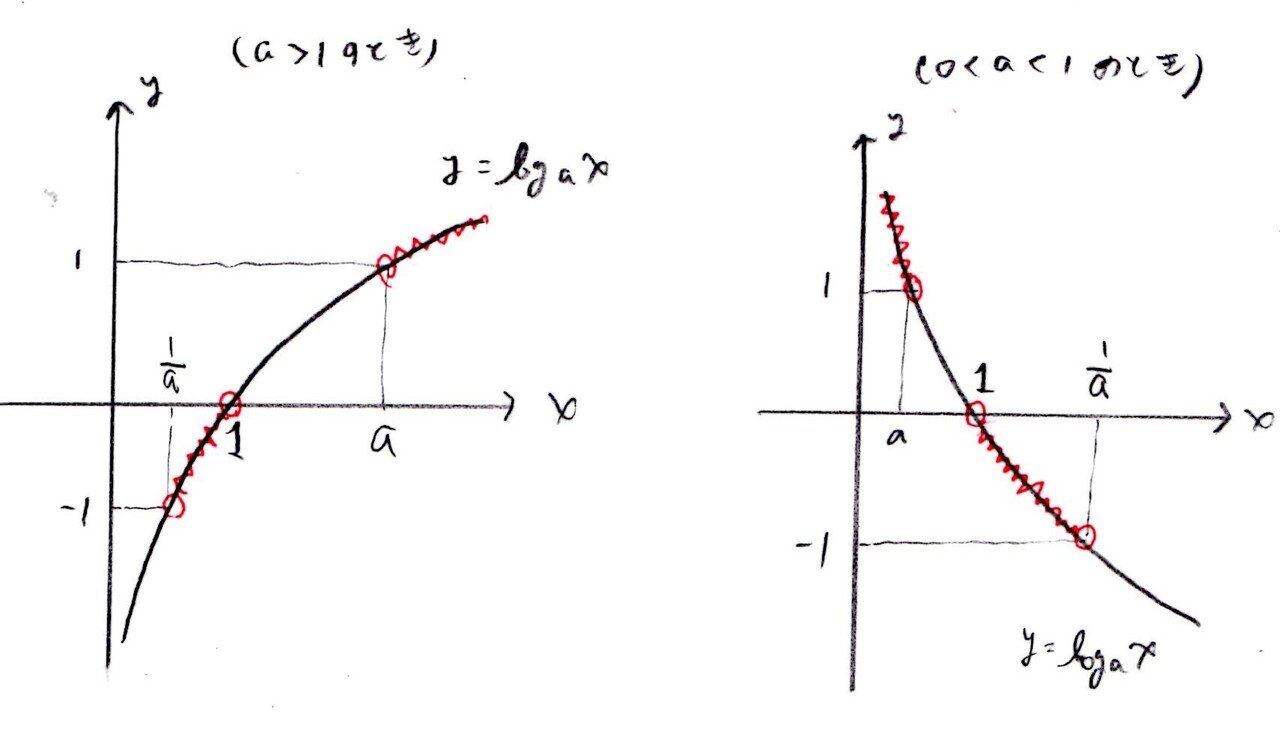
（4）やや易～標準
２
＜分析＞
(3)より、0<a<1のときのlogaｂとlogb aの大小関係が出ました。選択肢の底はすべてpです。
1/p＝13/12≒1.083、q＝12/11≒1.091、r＝14/13≒1.077に注意して比較検討すると、大小関係が求められます。
第２問
[１]
【解答】
(１) 易
(ア) １、(イ) ０
＜分析＞
f'(x)＝3x²-6aであり、a=0のときf'(x)≧０、a<0のときf'(x)＞０。両者とも単調増加ですが、前者では接線の傾きが一瞬０になります。
（２) やや易
(ウ) ３、(エ) ２
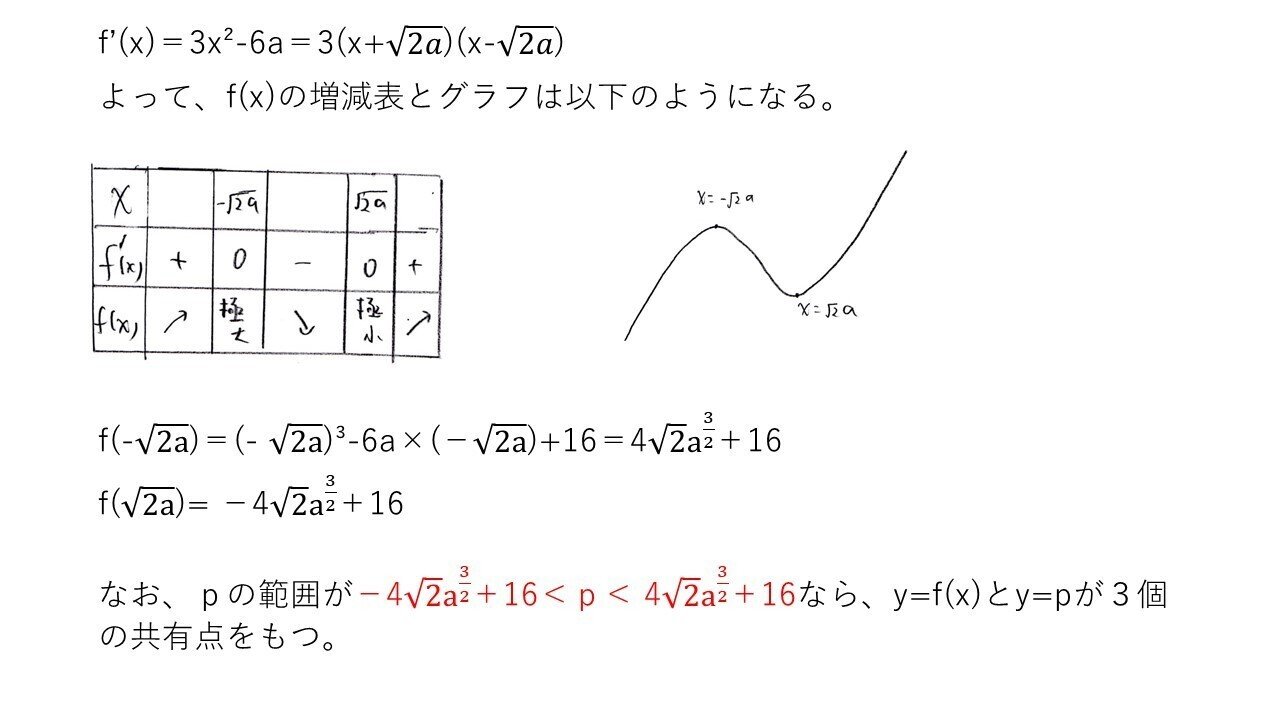
＜分析＞
a>0のとき、f'(x)＝０を満たすxは２個存在することから、増減表を書けばグラフの概形も描けます。よって、条件を満たすpの範囲も求められます。
(３) 標準
(ケ)１、(コ) ４
＜分析＞
(1)の結果の利用、反例を挙げる等の作業により、1,4以外の選択肢の誤りを指摘すれば解けます。
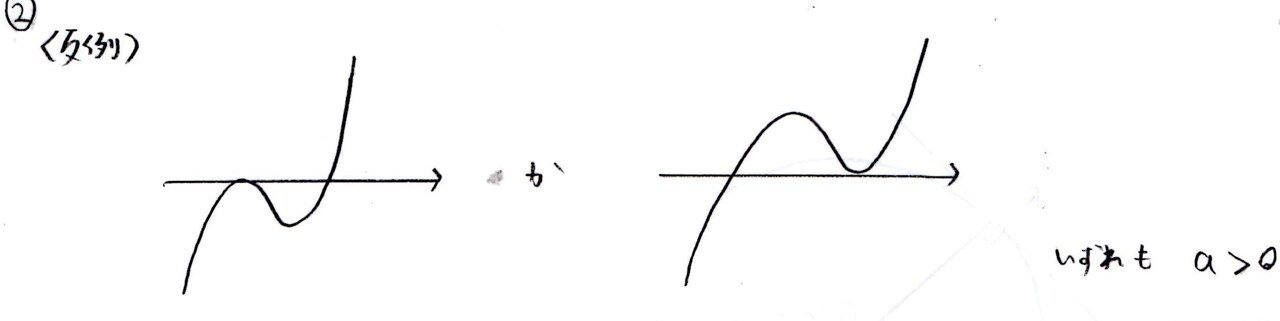
[２]
【解答】
(サ～ス) 易
＜分析＞
g(x)＝h(x)を解くだけです。２次方程式になるので簡単。
(セ)～(タ) 易～やや易
(セ)２、(ソ)１、(タ)２
＜分析＞
これはC₁とC₂の大小関係を調べて概形を書けば簡単です💡
(チ～ノ) やや易
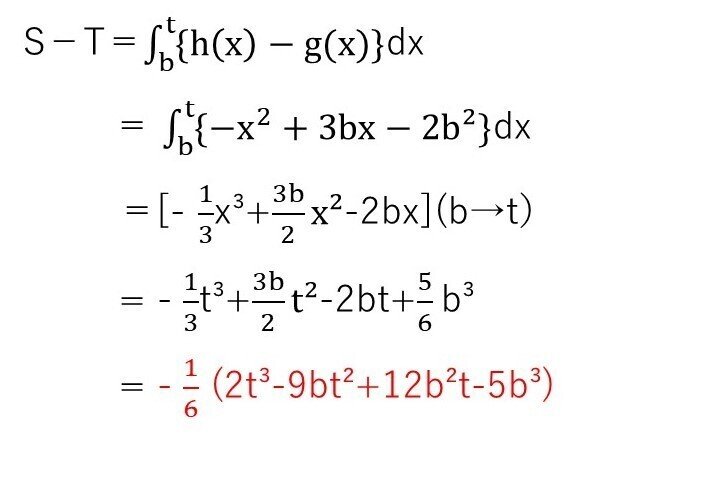
＜分析＞
(タ)で出た式を具体的に計算するだけの問題です。なお、t=bでS＝Tが成り立つのは、積分範囲がbからtであることから読み取りましょう🧐
第３問
確率分布は未修でわかりません、ごめんなさいm(__)m
第４問
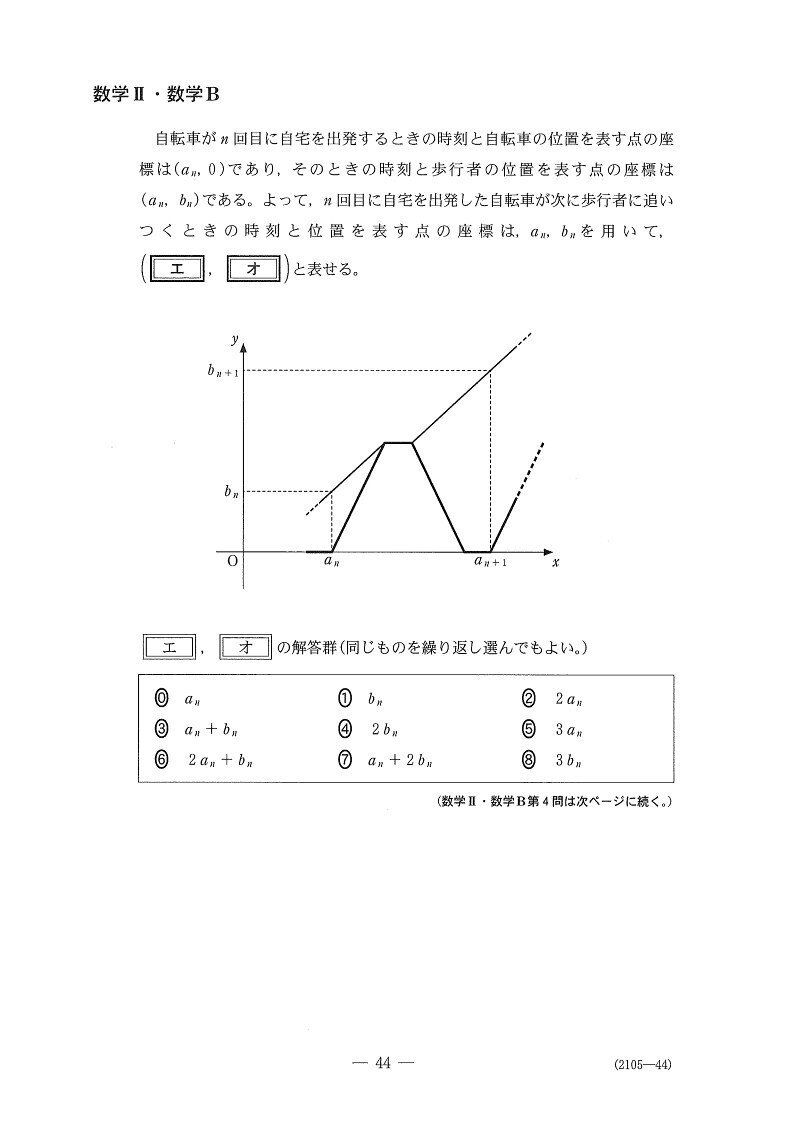
【解答】
[１]
(ア～ウ) やや易
(ア) ４、(イ) ８、(ウ) ７
＜分析＞
まず問題条件の解読に手間取りますね💦しかし、条件に従って、歩行者と自転車を動かせば数値は出ます。詳細は下図参照👇
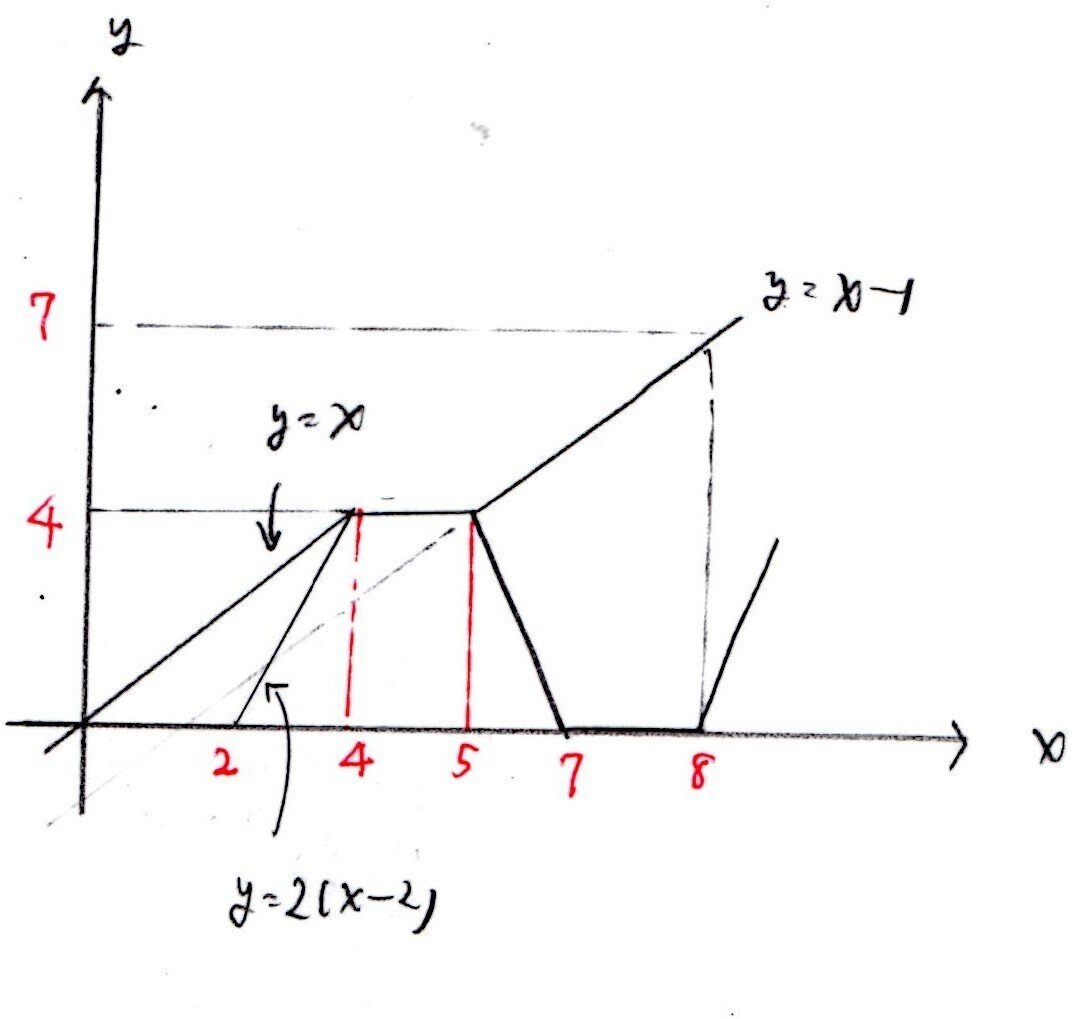
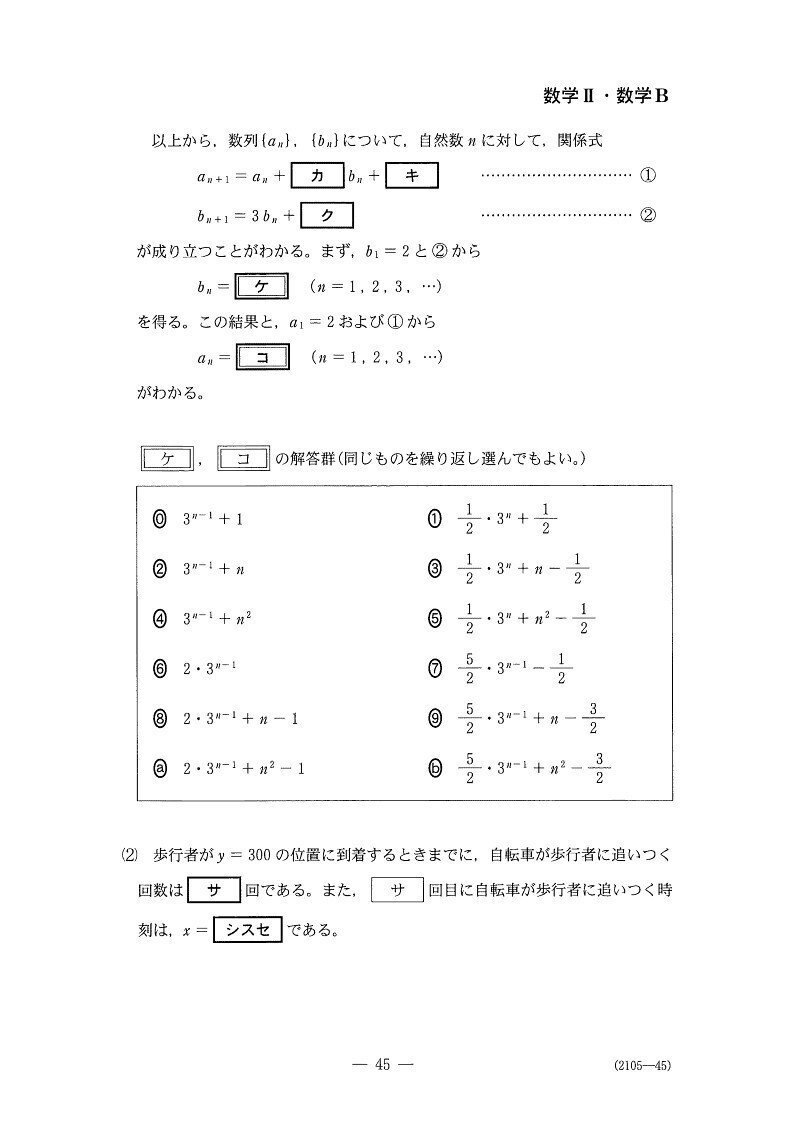
(エ～コ) 標準
＜分析＞
自転車の動きを正確に把握すれば、丁寧な調査により漸化式は立ちます。とはいえ、共通テストにしてはややレベルが高いかな～💦
漸化式は誘導通りまずｂnを求めます。その後、anを解答のように引き算を足す形にして導出します。
[２]
(サ～セ) 標準～やや難
＜分析＞
(ケ)(コ)の正解が前提なので、やや難度は高いです。
ここでは、自転車が歩行者に追いつくときのy座標が300以下となるnを求めるとスムーズです。
時刻はx座標を求めるといいですね。
第５問
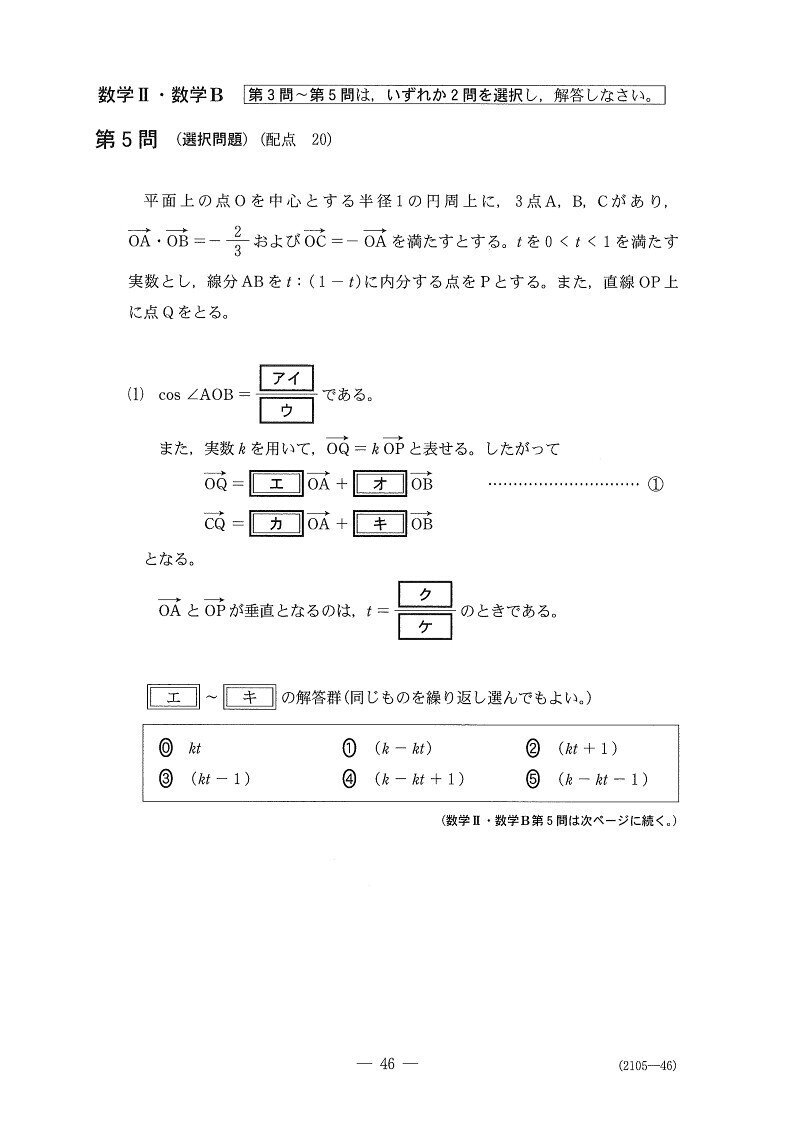
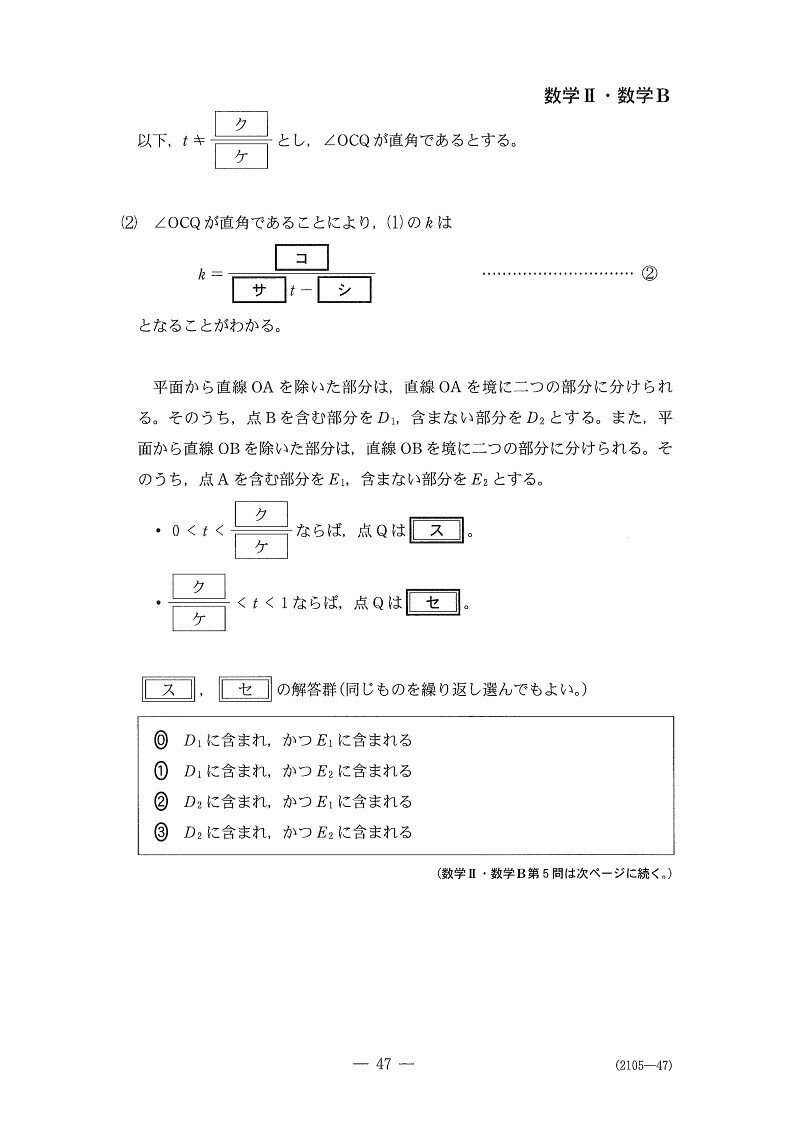
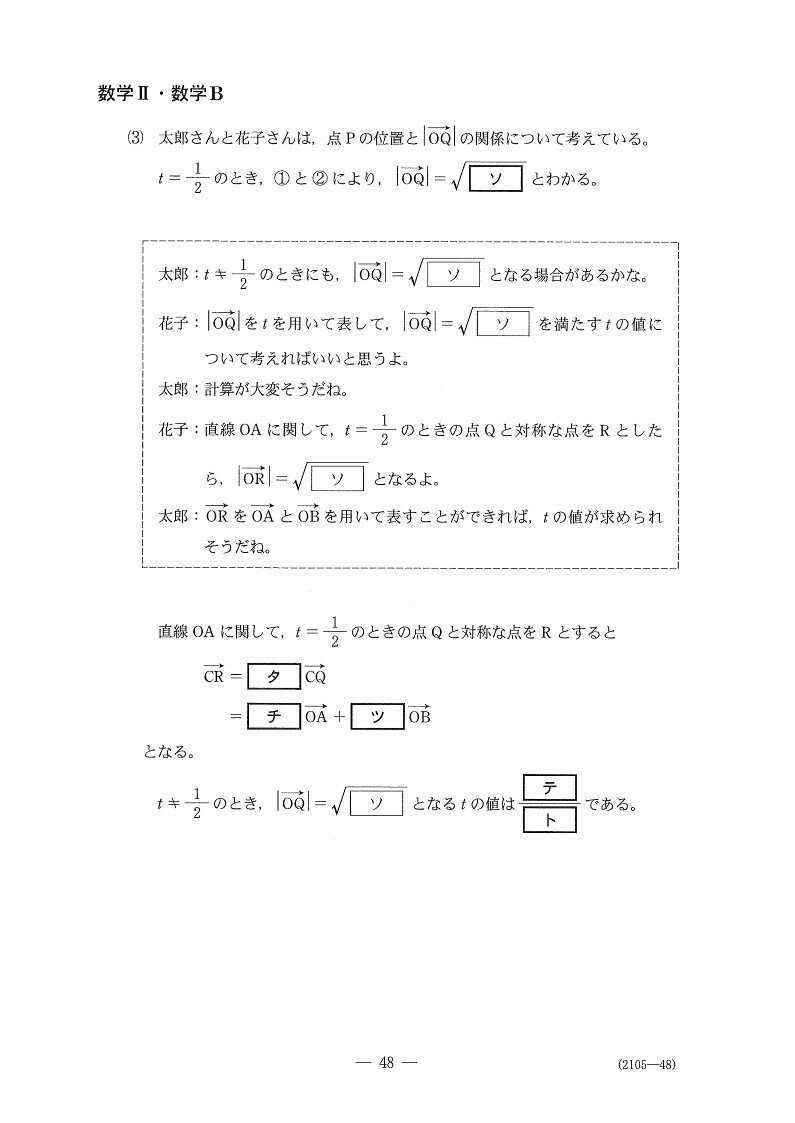
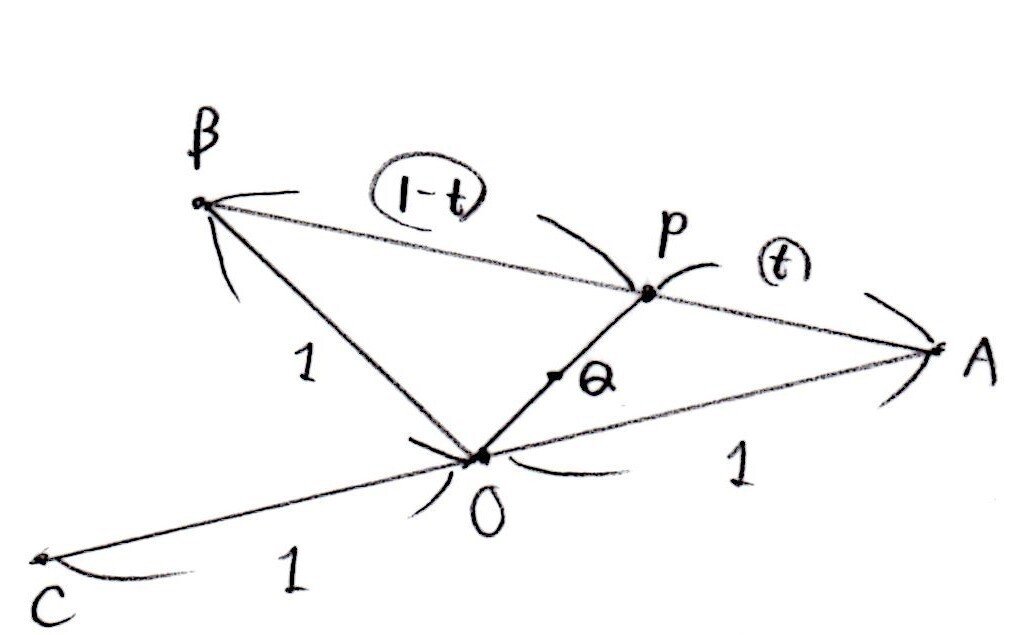
まず様々な条件を図式化します✊
【解答】
[１]
(ア～ケ) 易～やや易
＜分析＞
cos∠AOBの値は、内積の定義を知っていれば簡単に出ます！内分点のベクトル表記、垂直条件は基本事項なので、問題ないでしょう。
[２]
(コ～シ) やや易
＜分析＞
扱いやすいのはOA,OBなので、内積OC・CQをOA,OBのみを使って表す工夫をしましょう💡
あとは、お馴染みの垂直条件でｋの値は出ます！
(ス)、(セ) 標準
３,０
頭で考えるより丁寧に図を描いた方が速いです。直線OAをℓ₁、直線OBをℓ₂として、k>0の場合とk<0の場合を図示すると下図のようになります👇
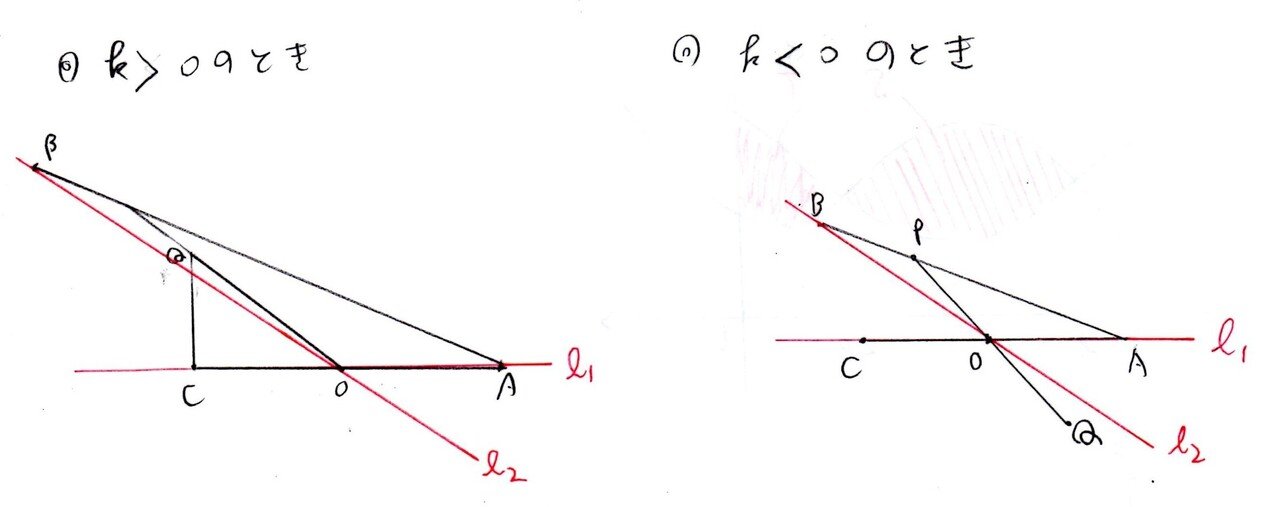
[３]
(ソ～ツ) やや易
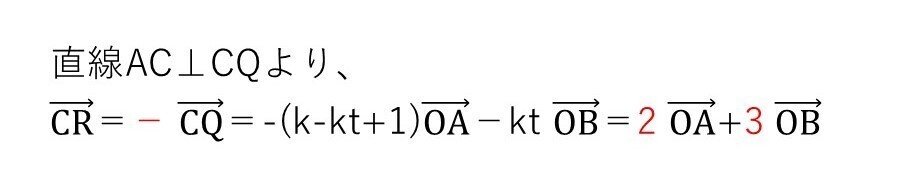
＜分析＞
①,②を用いる誘導があるので、k,tの具体的数値を代入してOA,OBのみの表記にすれば答は出ます。
(テ,ト) やや難
＜分析＞
Rは直線ACに関するＱの対称点で、OR=√6となるtを求めればいいのです。
kを消去してｔだけの式にしますが、この処理がなかなか厄介ですね～。計算の煩雑さに心が折れた受験生も多くいたことでしょう💔
総括
以上で、共通テスト数学ⅡBの解説を終わりますm(__)m
センター試験含め、直近５年間ではやや難しい回ですね。
難易度自体は2013年,2015年と大差ない感じですが、量が多いのと題意把握に手間取る点で、体感難度はより結構高く感じたのかな？と思います💔
手間取り箇所は・・・第１問[２]の最後、第２問[１]の最後、第４問の漸化式、第５問の最終問ですかね。
