
受験生の皆さん、こんにちは!
東大合格ビジネスマンのワタシですm(__)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ 3大基礎力重視の裏ワザ勉強法
について、様々な観点から発信しております。
今回は、凶悪難易度ゆえ物議を醸した2022年共通テスト数学ⅠAを徹底解説していきます🤥✊
2022年度は全体的に難化しましたね・・・実際、東大受験生平均点も嘘のようにガタ落ちしております。
私自身が現役プレイヤーなので、学校の先生や予備校講師といった指導者目線ではない、プレイヤー目線でまた違う徹底的に語りつくすことができるのでは?
と思い、解説記事を作成しましたm(__)m
私の公式LINEでは、無料相談を随時受け付けております。
公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってください✊
私も苦手科目は先生に頼りました。
また、LINE登録していただいた方には
無料プレゼント(1年で偏差値70出す画期的勉強法)
を贈呈します🎁
【⬇️公式LINE登録はこちら⬇️】

しかし、1つお詫びがあります・・・
実は、[2] データ問題、[5]平面図形は私未修でわかりません・・ごめんなさいm(__)m
[5]は平面図形というより、メネラウスの定理・チェバの定理がわからん!と言った方がよいか(笑)
では、早速問題を見てみましょう👀
第1問
[1]


【解答】
(1) 易
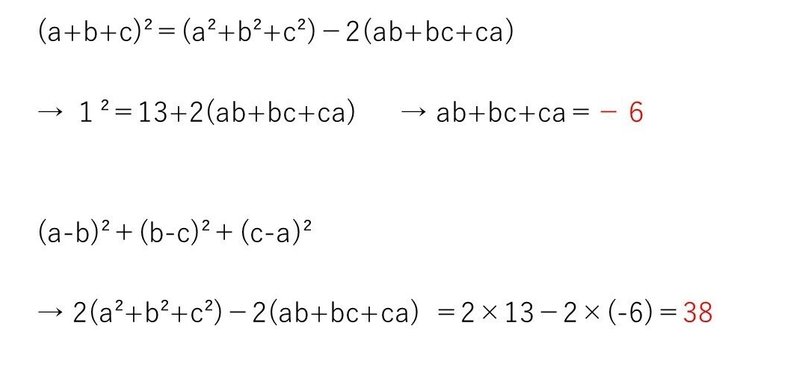
(2) やや易

<分析>
有名な対称式の変形。
(1)は素直に展開すれば解法が見える、(2)も誘導に従えばx²+y²とx+yの値が出るので、xyは求められます!
[2] やや易
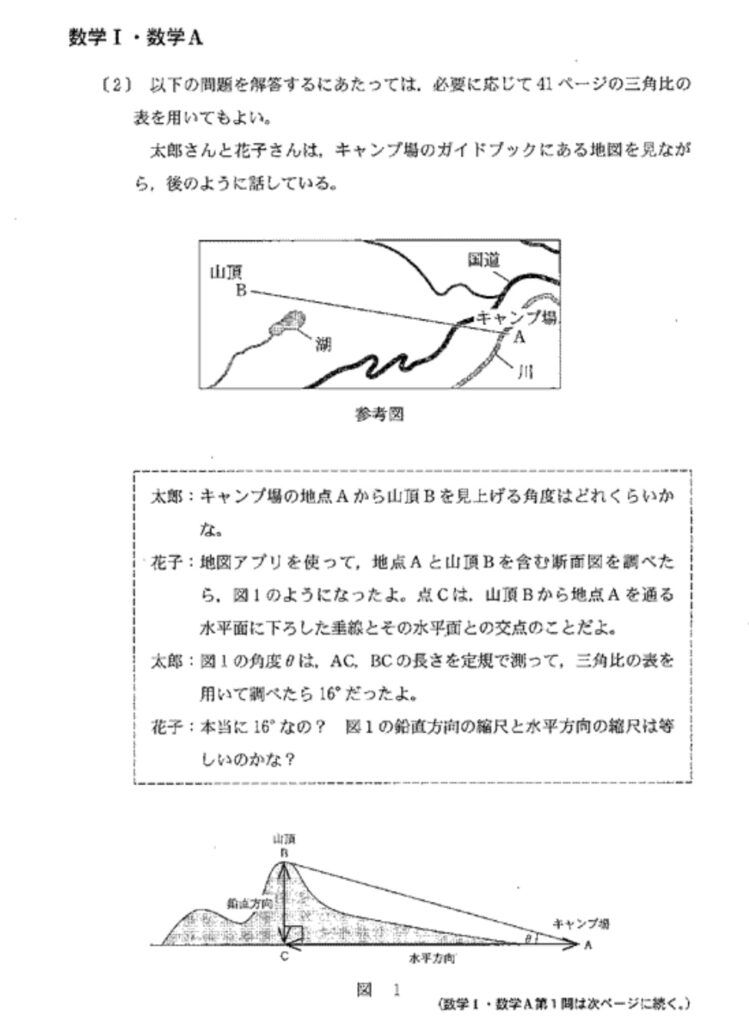

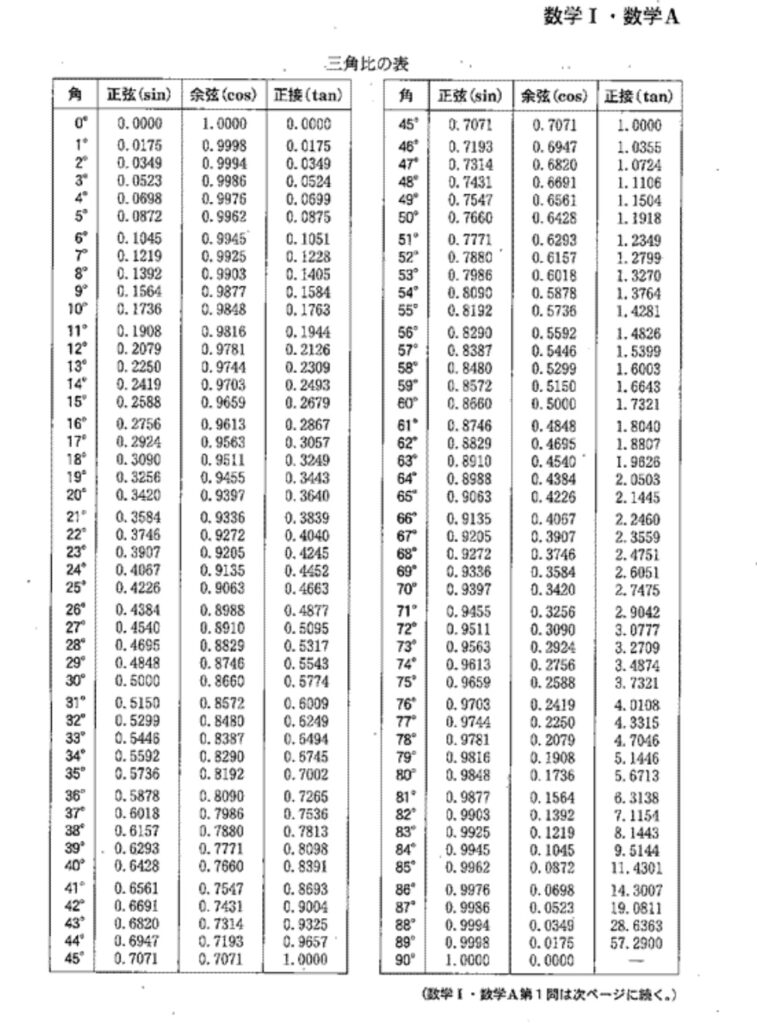
【解答】
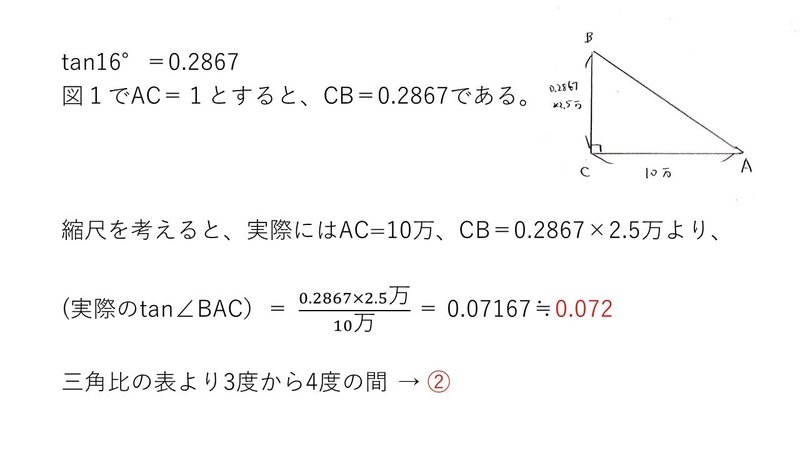
<分析>
おお、地理ではなく・・・まさかの数学で縮尺登場ですか。
これは縮尺の意味がわかれば何てことない問題ですが、「縮尺って何?」ってなった不勉強な受験生は思わぬ失点をしたことでしょう😅
[3]
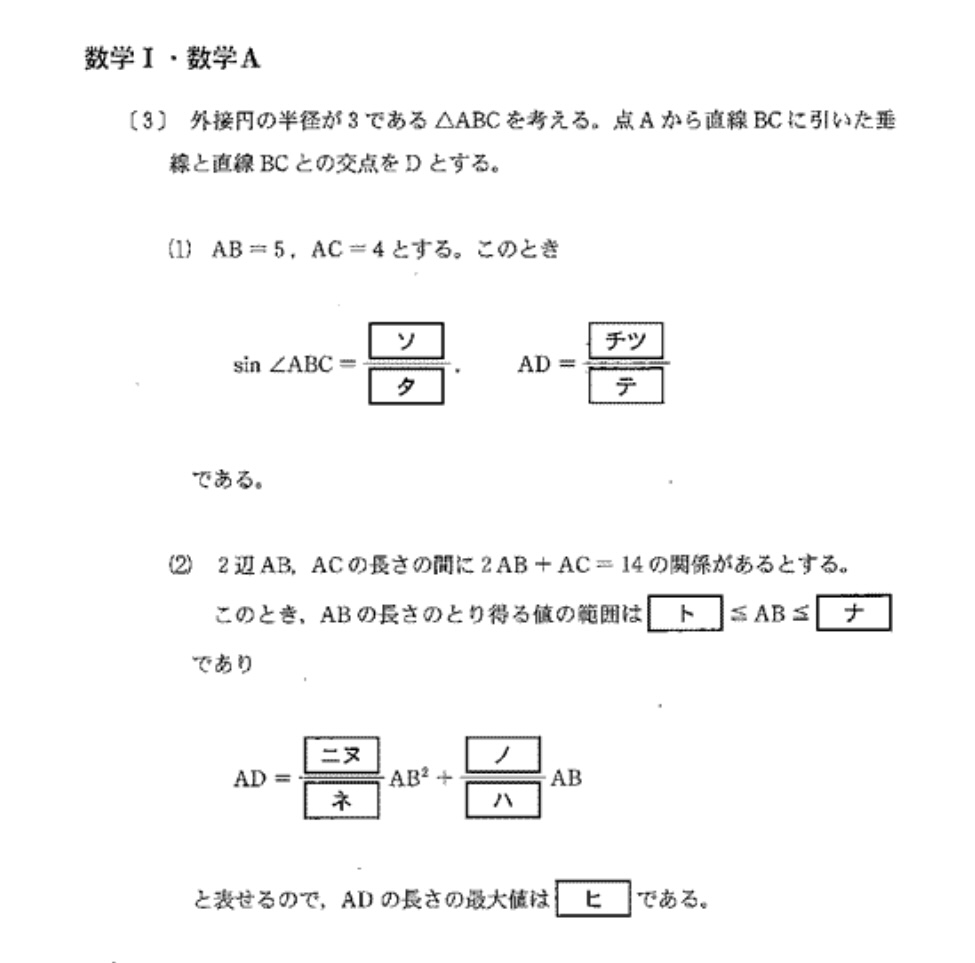
(1) 易~やや易
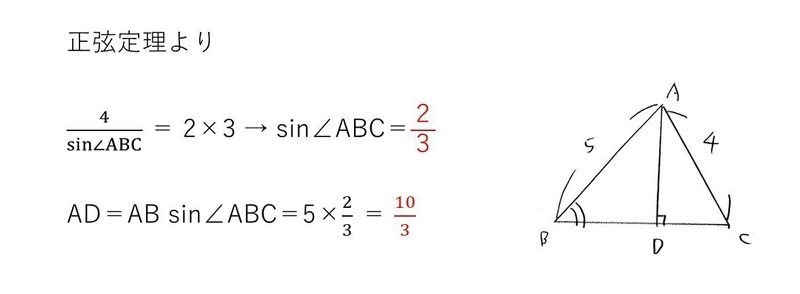
<分析>
三角比で外接円の半径と来たら正弦定理が定石。ADは△ABDが直角三角形より出せますね。
(2) 標準~やや難


<分析>
ABの最大,最小を絞るのが難しかったでしょう💦
ABの最大値は正弦定理とsin∠ABC≦1を用いて出せて、ABの最小値はACの最大値を求めることで出せます。
後半は、条件式よりACを消去するとABに関する二次関数に帰着できますね!平方完成して出しますが、ABの範囲に注意しましょう。
第2問
[1]


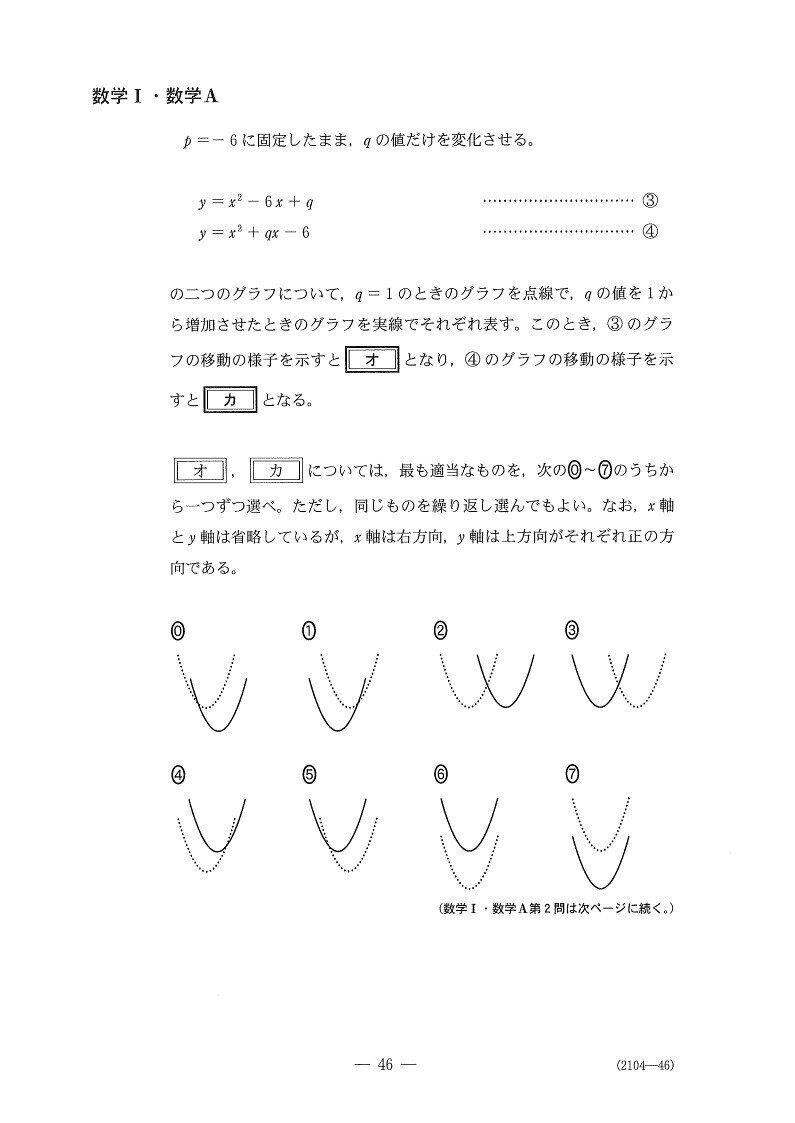

この2人どういう関係?

(https://stampo.fun/s0018_9/より引用)
あ、何でもありません。では、以下解説いきましょう!
【解答】
(1) 易

<分析>
p,qの値が与えられているので、代入して2次方程式を解くだけです。
(2) 標準


<分析>
問題の誘導より、共通解αを使う解法だとα=1またはq=-6が出ますが、q=-6だと不適と判断してα=1→ q=5を確定します。
後半の発想が共テにしては難しい💦
前半のq=5の場合を調べると、「①,②はともに異なる2つの実数解をもつけど、一方は共通解」の状況になっています。では、その他にn=3となる場合は?と考えると・・・「①が重解,②が異なる2実数解をもつ」状況ですよね☝
(3) やや易

<分析>
平方完成して、頂点のqに関する動きを調べると比較的簡単にわかります。
(4) 標準~やや難
キ→3
ク→1
<考え方>
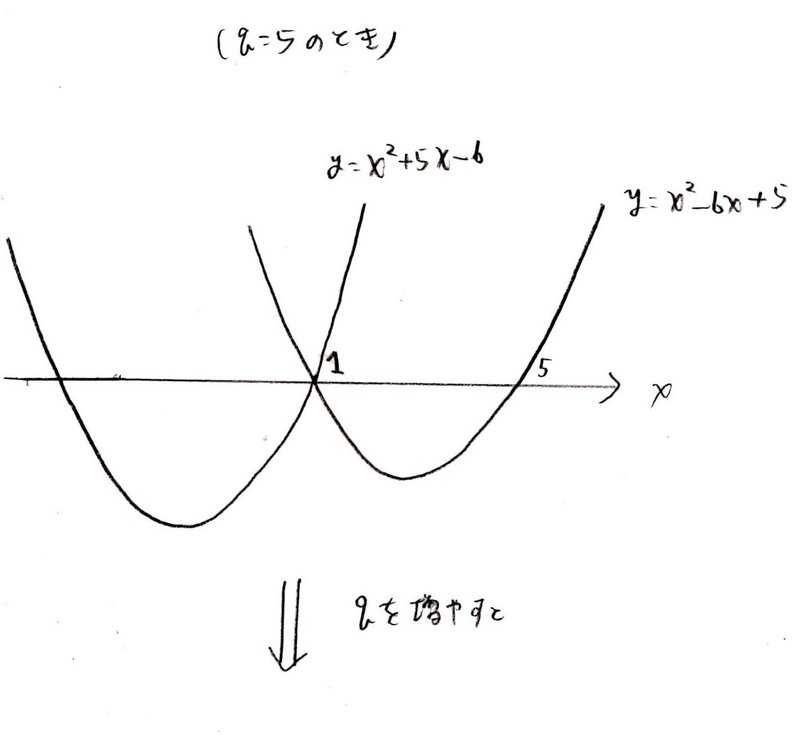
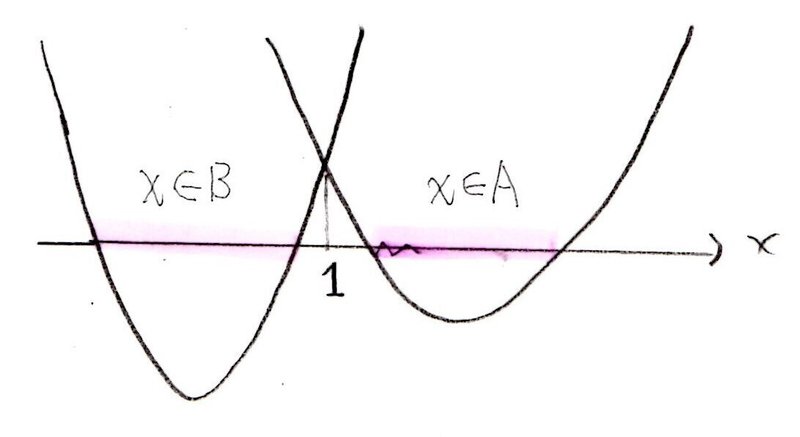
<分析>
まず、必要条件・十分条件の意味はわかってますか?これです👇
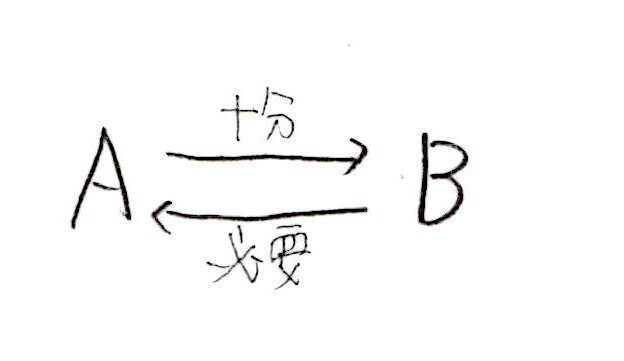
脳内処理すると混乱するので、図示して調べましょう。
qの範囲が5<q<9で、(3)でqを増加させたときの2曲線の動きを調べたことを考慮すると、「q=5の状況を図示する ⇒ qを増やすときの条件式を満たすxの変化を調べる」の手順を踏めばよいことがわかります🤔
[2]
データ問題は未修でわかりません・・ごめんなさいm(__)m
第3問


参加者全員が自分以外のプレゼントをgetすれば終了するらしいですね。
これ無制限なんですか(笑)?参加者30人、回数エンドレスでやったら・・・次の交換会はないな~!
「帰れまTen」状態になり、苦痛でしかない🤥

(https://www.bg-ranking.xyz/category/tv/kaerema10/より引用)
【解答】
人をA,B,C,D,Eとし、各人の持参したプレゼント🎁をa,b,c,d,eとする。
(1)
(ⅰ) 易

(ⅱ) 易

(ⅲ) 易~やや易

<分析>
直接求めるのが大変な場合は、余事象の利用を意識します!
3人で交換会しても約20%の確率で4回で終わらんとはね・・さすがに4回以上は飽きるでしょ🤥💨
(2) やや易


<分析>
解法は<構想>で与えられているので、それに従って解くのみです。
参加者がA~Dの4人いるとして、「A~Dの誰が?」「残りの人はどうなればいいか?」に着目すれば解けます。
残りの人については、(1)の結果の利用を考えましょう💡
(3) やや易~標準


<分析>
4人が5人に増えただけで、考え方は(2)と全く同じ。(2)ができれば芋蔓式にできるでしょう。
(4) 標準

<分析>
(3)の正解が前提。条件付き確率なので、(4)の確率では「分母はA~Dが自分以外のプレゼントを受け取る確率」になります。A~Dの条件は決まっているので、あとはEが自分のプレゼントを受け取るか否かで場合分けすればいいですね。
条件付き確率の定義は大丈夫ですか🤔❓理解が曖昧だった方は、よく理解しておきましょう。
以下の図がシンプルでわかりやすいと思います。本問では、事象A={A~Dが自分以外のプレゼントを受け取る}、事象B={Eが自分以外のプレゼントを受け取る}、条件付き確率=P(A∩B)/P(A)と定めることができます☝
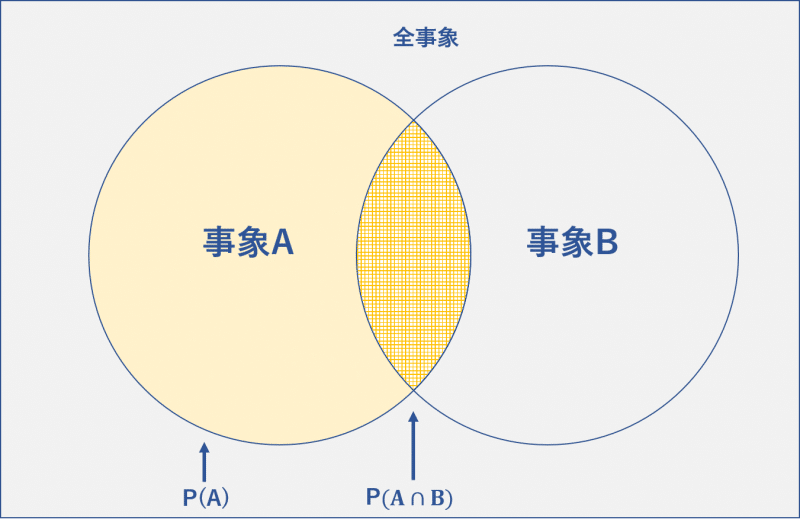
※ P=Probability
第4問


【解答】
(1) やや易

<分析>
共テの最初の問題にしてはやや難しめですが・・・整数問題としては定石的な解法。
「互いに素」を利用するこの解法は頻出なので、よく身に付けておきましょう☝
(2) やや易

<分析>
後半の表記は①’の式を利用しています。誘導型の問題では、「この小問では何をやらせたいのか?」を意識することが大事です。
(3) 標準

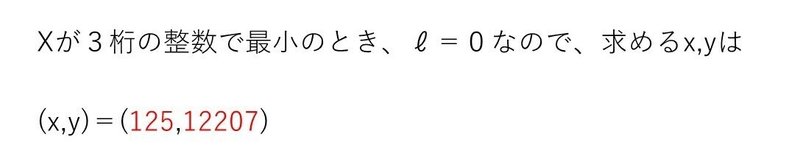
<分析>
「5⁵と2⁵と1を含む式を導出するにはどうすればよいか?」を考えると、(2)の2つの式を引き算すればいいのかな?と推測できるでしょう。
ただ、数値計算が結構汚い!余程自信のある受験生でないと、「本当に合ってるのか?」と疑問視するのも無理はないかと💦
(4) やや難


<分析>
これは難しい・・・旧帝大の二次試験で出ても骨のある問題🦴
数値計算も汚いし、(2)(3)と同じノリで解いていると「あれ?xが2桁にならね~、間違えたんか?」な結果になったことでしょう。
本問では偶奇を意識したいですね👀
2y=11⁴m+915の形より、「mが奇数でないとyは整数にならない!!」点に気付く必要がありました💦
第5問
メネラウスの定理、チェバの定理がわからんので、平面幾何も省略させてください・・・すいませんm(__)m
中学受験してないからなのか?マジでわからんのですよ💦
以上で、数学ⅠAの解説を終了します。データの分析、平面幾何をスルーしてしまう東大合格者もなかなかいないだろう。
諸々の業務が落ち着いたら、腰据えて学習します!
総括
以上で数学ⅠAの解説を終わりますが、確かに今年は難化していました。
全体的に見ると、第1問,第2問はまだ穏やかですが…
第3問はどこかで躓くと後が雪崩起こす、第4問は計算も重く数値も汚く途中で挫折した受験生が多かったでしょう💦
最後に、再度公式LINEの紹介をします。
公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信する公式LINEはこちら👇
登録していただいた方には、無料プレゼント贈呈🎁の他、無料相談も受け付けております。






