
受験生の皆さん、こんにちは。
東大合格ビジネスマンのワタシですm(_ _)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ 3大基礎力重視の裏ワザ勉強法
について、様々な情報を発信しております📢
私の公式LINEでは、無料相談を随時受け付けております。
公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってください✊
私も苦手科目は先生に頼りました。
また、LINE登録していただいた方には
無料プレゼント(1年で偏差値70出す画期的勉強法)
を贈呈します🎁
【⬇️公式LINE登録はこちら⬇️】

you tube版がこちら👇
問題
【第1問】

【第2問】

【第3問】

【第4問】

【第5問】

【第6問】

解答解説
【第1問】
(問1)
易~やや易
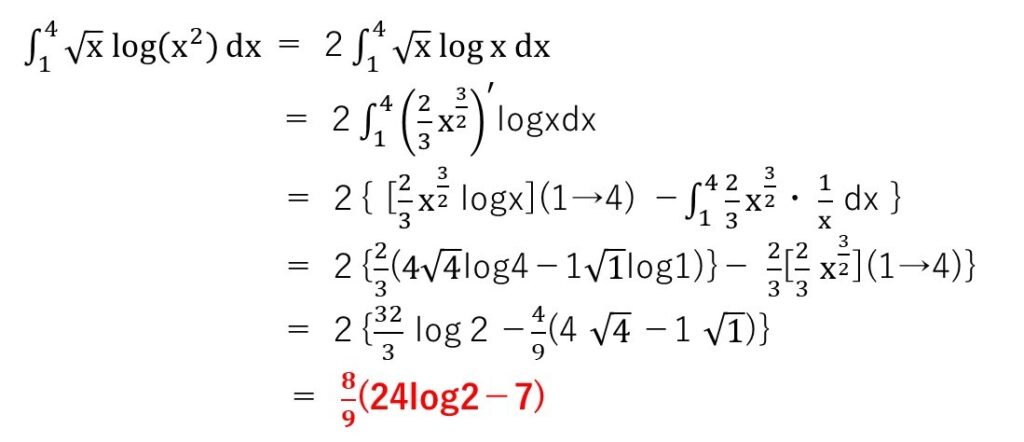
logが絡む積分は部分積分が鉄則です。これは数Ⅲの積分計算になじみがあれば簡単に思いつくでしょう。√xはxの1/2乗と解釈すれば、あとは計算ミスに注意するだけ。
本問はただの計算問題なので、外すと即0点だと覚悟してください!!
(問2)
やや難
<解答1>


<解答2>
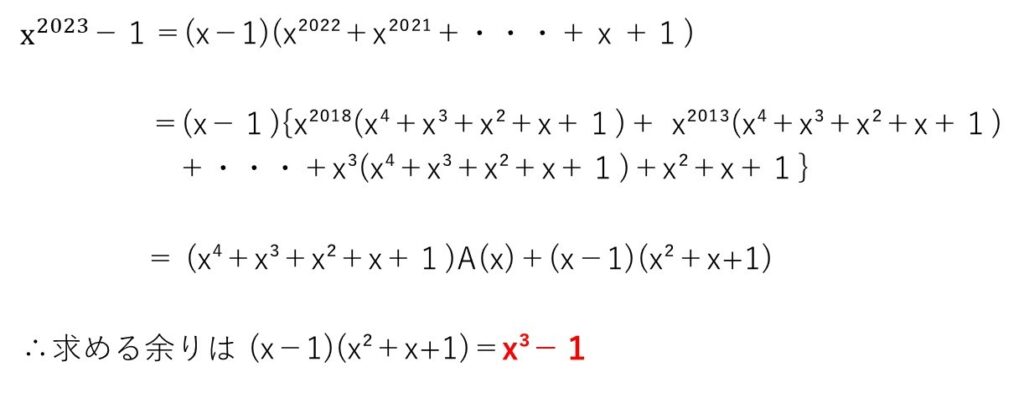
予備校評価では「やや易~標準」となっていますが、実際に受けた受験生はやや難しく感じたでしょう。
(解答1)
x²+x+1=0の解が1の3乗根であるのは十分演習を積んだ受験生にはおなじみでしょう。よって、今回もx⁴+x³+x²+x+1の形も1の5乗根(αとおく)を意識できれば、余りQ(x)についてQ(α)、Q(α²)、Q(α³)、Q(α⁴)を求めることでQ(x)=x³-1だろうと推測するのは可能だったでしょう。
しかし、これだけでQ(x)=x³-1と決めつけるのは気が早いです。Q(x)がx³-1以外の整式になりえないことをきちんと論証しないと、減点答案です。
では、どうするか?というと、新たに整式R(x)をR(x)=Q(x)-(x³+1)と定めるのです。すると、R(α)=R(α²)=R(α³)=R(α⁴)=0となり、R(x)が3次以下の整式であることから、R(x)は0以外にありえなくなります。これでQ(x)=x³-1と確定するのです。
(解答2)
xn−1のよくある因数分解を用いました。(x-1)でない方の因数を5個ずつx⁴+x³+x³+x+1の形を作ってまとめることで、最終的な余りは(x−1)(x²+x+1)=x3−1と求められます。
【第2問】
やや易



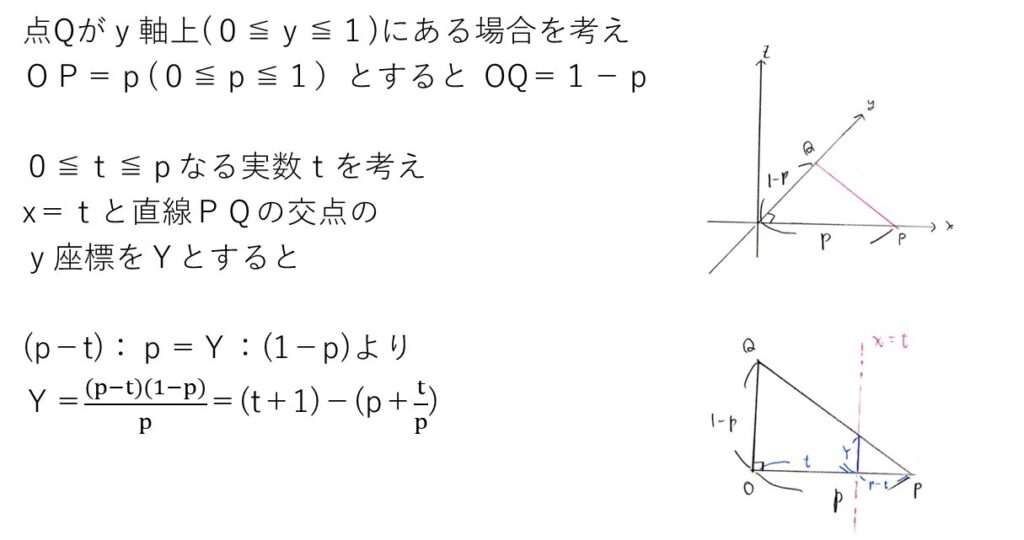
問題文の条件より、OP→、OQ→、OD→はa→,b→,c→を用いて表せます。
次に、点Xが直線CPと直線QRの交点であることから「点Xが直線CP上かつ直線QR上」と捉え、OX→を2通りで表すことを考えます。
すると、係数比較により方程式が3つ立式でき、未知数がk,ℓ,mの3個より各値を求めることができます。
【第3問】
(問1)
易

Yはサイコロの目の積、5は素数より、5が1回でも出るとYは5の倍数となります。
よって、余事象「5が1度も出ない確率」を求めれば1発解決します。
共通テストでも簡単なレベルなので、必ず取りましょう🚩
(問2)
やや易〜標準

15=3×5より、3 or 6 と5がともに1回でも出ればYは15の倍数となります。
5が1回も出ない確率は(問1)で求めたので、ここでは「5が出るけど3 or 6が1度も出ない確率」を考えて、(問1)と同様に余事象的に求めると解きやすいと思われます。
【第4問】
標準



本問も簡単っちゃ簡単なのですが、「相加相乗平均の関係から最小値2」に飛びついた受験生は大幅減点を免れないでしょう。
何がダメか? それは
①等号成立条件のg(x)=1となるxが-1≦x≦1にあるか調べていない
②f(x)を実数全体を定義域とする連続関数として扱っていない
からです。
g(x)の範囲を求めた後も注意が必要で、ここでも何となくx=0で最大でx=±1で最小と決めつけると減点対象です。
解答のようにf(x)が−1≦x≦1で微分可能な連続関数であることを示したうえで、最大最小に言及すべきです。
【第5問】
やや難~難


本問は類題経験があれば有利でしたが、京大入試ではあまり出ないタイプの問題です。実は、2016,2017年の東大理系数学第6問に類題があったので、よく勉強していた受験生にとってはかなり有利だったと思われます。
京大対策ばかりしてきた受験生を弾く秀逸な問題で、特に医学部医学科で合否を分ける問題になったでしょう。
【第6問】
(問1)
易

(問2)
難



(1)
3θ=θ+2θ,4θ=2θ+2θより、加法定理と2倍角の公式を利用すると、cos3θ,cos4θともcosθで表すことができます。(2)
本問は「チェビシェフの式」を意識できた受験生には思い切り有利な問題でしたが、そうでない受験生には難問でした。医学科でも捨て問でいいでしょう、これは😅😅
京大は(1)を誘導のつもりで出したのだと思いますが、受験生に誘導の意図を気付かせるにはレベルが高すぎます。
繰り返しになりますが、私の公式LINEでは無料相談を随時受け付けております。
また、LINE登録していただいた方には、無料プレゼント(1年で偏差値70出す画期的勉強法)を贈呈します🎁




