
受験生の皆さん、こんにちは。
東大合格ビジネスマンのワタシですm(_ _)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ 3大基礎力重視の裏ワザ勉強法
について、様々な情報を発信しております📢
私の公式LINEでは、無料相談を随時受け付けております。
公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってください✊
私も苦手科目は先生に頼りました。
また、LINE登録していただいた方には
無料プレゼント(1年で偏差値70出す画期的勉強法)
を贈呈します🎁
【⬇️公式LINE登録はこちら⬇️】

2021年入試、旧帝大の第6弾は
「京都大学」です。
当ブログの解説記事は
読者が必死に3年間努力すれば
東大(理三以外)・京大(医以外)・九大医
レベルに80%以上の確率で合格できる
ことを目的に作成しています
市販の問題集のように、解法を丁寧に示すだけではありません!多角的なアプローチで問題を解きほぐしています✊
① 各問の難易度
② 他分野や一般常識との関連事項
③ 問題の躓きポイント
④ 極力曖昧な表現をしない説明
を示しています。
イマイチ成績が突き抜けられない受験生に貴重な情報が提供できればと思いますm(__)m
京大物理の特徴
京都大学の理科は2科目で180分。そのうち、物理は全3問です。
理科180分て長くない??
いやいや👋
下手に学力あって全問解きにいくと、情報処理に計算処理に思い切り時間食われて、むしろ足りないです🚩
今年の物理はまだマシだったと思いますが、それでも計算処理はそこそこ重い。
しかし、これで音を上げていては、難化した時が思いやられますね😵
内容をきちんと消化するには
全統記述模試の偏差値60~65程度
の実力が欲しいですね。
第1問
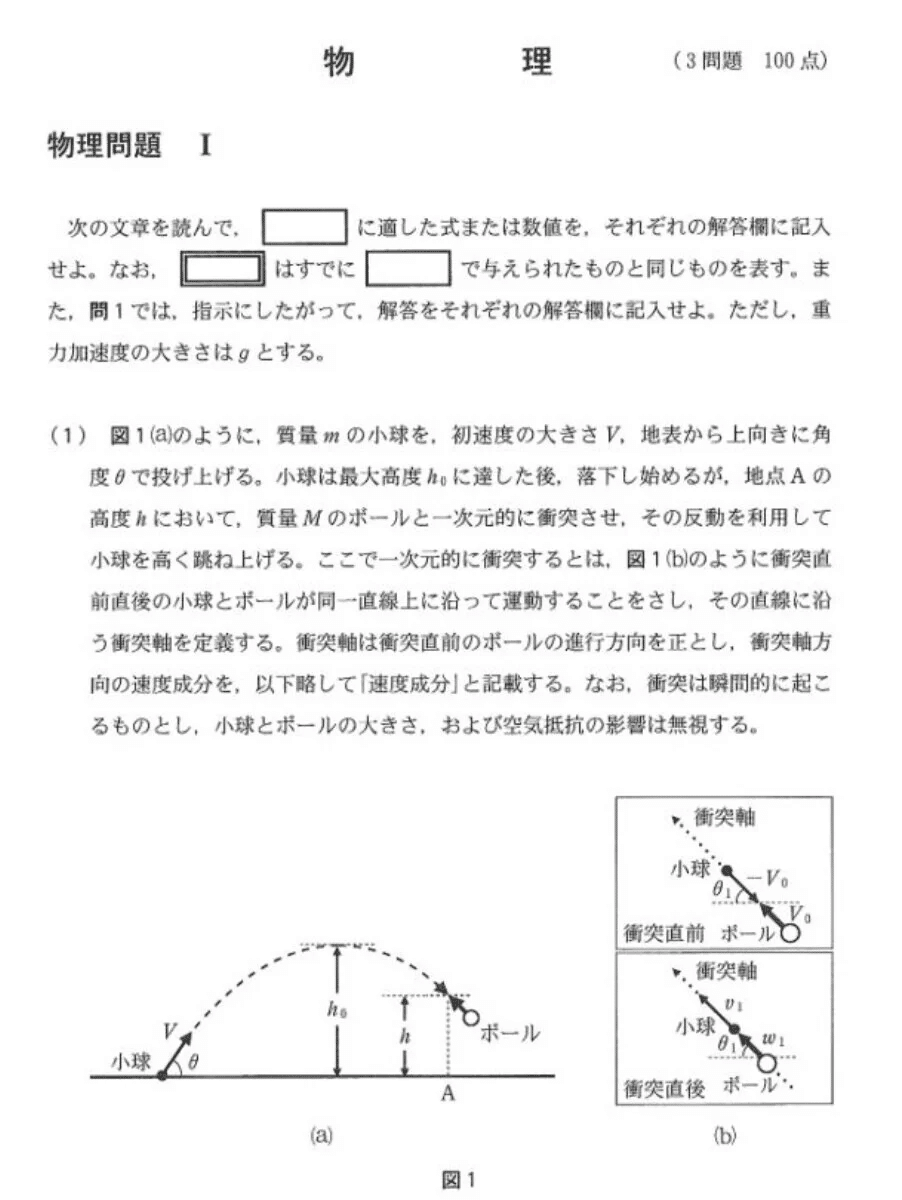


【解答】
(1)
(ア) 易
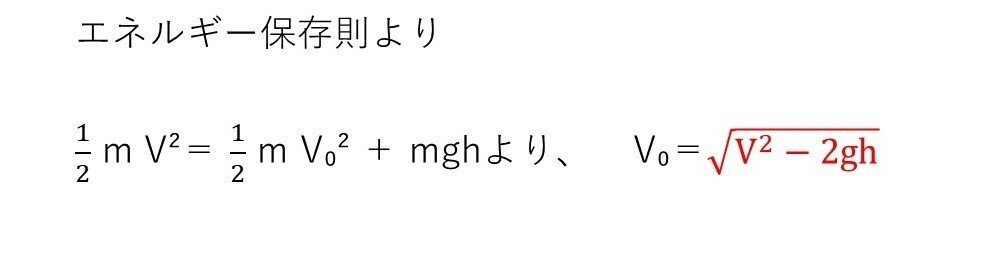
<分析>
超基本問題。大学受験生なら取れて当然な問題です💦
(イ) やや易
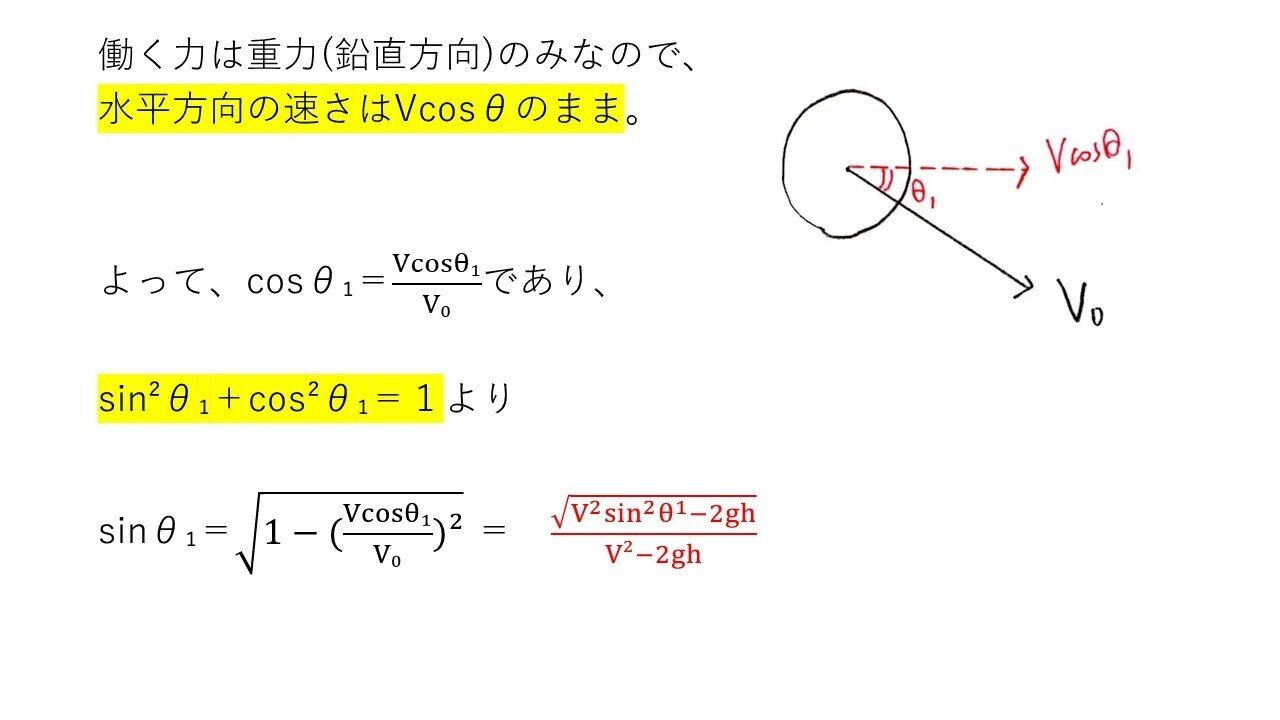
(訂正)
式の右辺は、cosθ₁,sinθ₁ ⇒ cosθ,sinθに変更
<分析>
θ₁は与えられており、まずcosθ₁が出ます。求めるのはsinθ₁なので、使う公式はsin²θ₁+cos²θ₁=1ですね💡
数学ⅠAが身に付いていれば、全然難しくない発想です🤔
(ウ),(エ) 易

<分析>
衝突時に出てくる定番の式「運動量保存則」「はね返り係数」を使うだけの問題です。
しかも、本問は誘導形式なのでさらに易しい😂
(オ),(カ) 易~やや易

<分析>
①,②はv₁,wを未知数とする連立方程式です。ただの中学数学(笑)
(キ) 易~やや易

(ク) 易~やや易
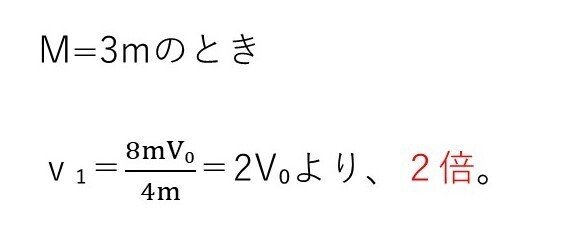
<分析>
前問ができれば、自動的にできます。
(ケ) やや易

<分析>
斜方投射でよく見る公式を使うだけの問題です。本問では、答に不要なV₀とsinθ₁を消去しましょう!
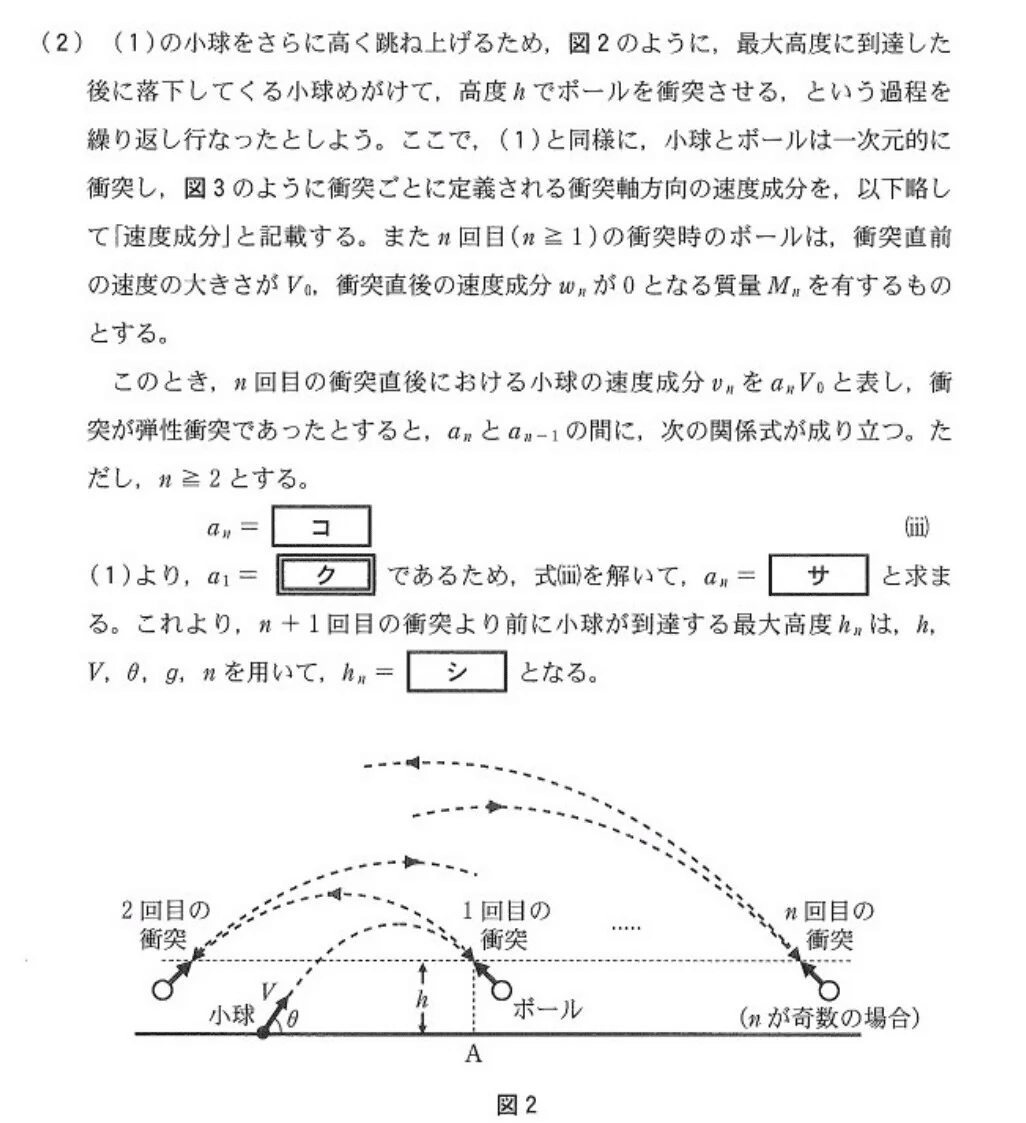
(2)
(コ) やや易~標準
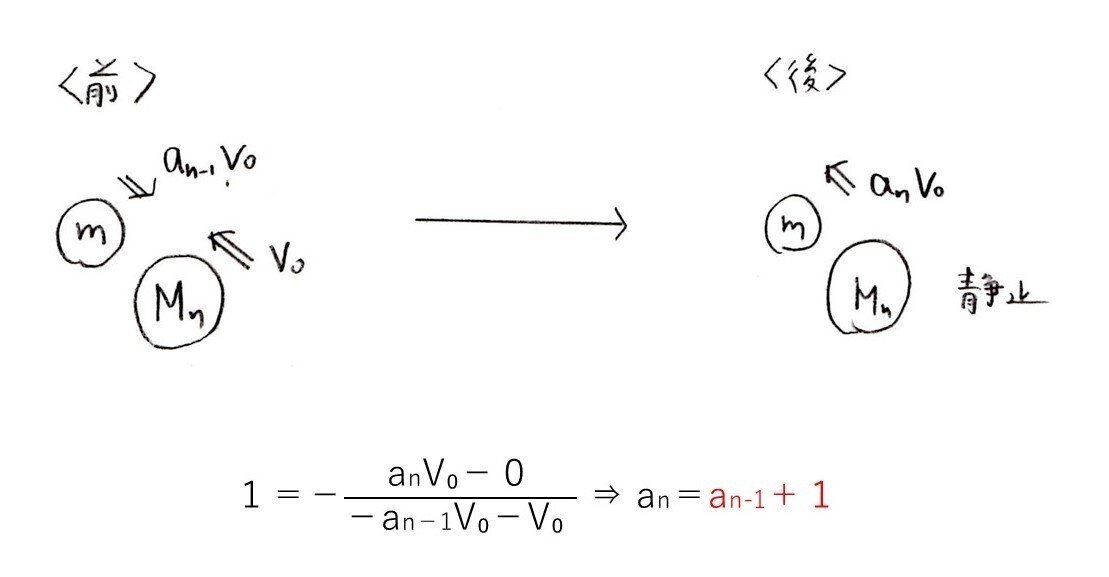
<分析>
m,Mが登場しないことに着目して、「m,M不在だし、跳ね返り係数の式を使うっぽいな♪」と推測するのもアリでしょう😳
(サ) やや易~標準
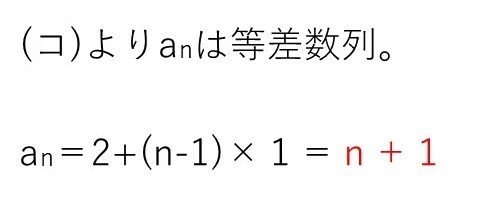
<分析>
(コ)ができれば楽勝👋
(シ) 標準

<分析>
(サ)でn回目衝突直後の小球の速さが出たので、(ケ)と同様の解法で高さhnを求めることができます!
(問1) やや易~標準

<分析>
これも(コ)ができれば楽勝👋
(問2) 標準

<分析>
(シ)ができれば解答可能です!hnが出れば、あとは不等式を満たす最大のnについて調査すればOKですね💡
最終問題にしては結構易しめ。
<感想>
(1)はすべて典型問題なのでしっかり取る。
(2)の(コ)はM.,mが答に出ないことがはね返り係数を使えというヒントになっています。(シ)は水平方向となす角を意識すればできますが、少し難しい。とはいえ、問2まで見た限り、大問としての完答難度は低めかな~と思います🧐
第2問

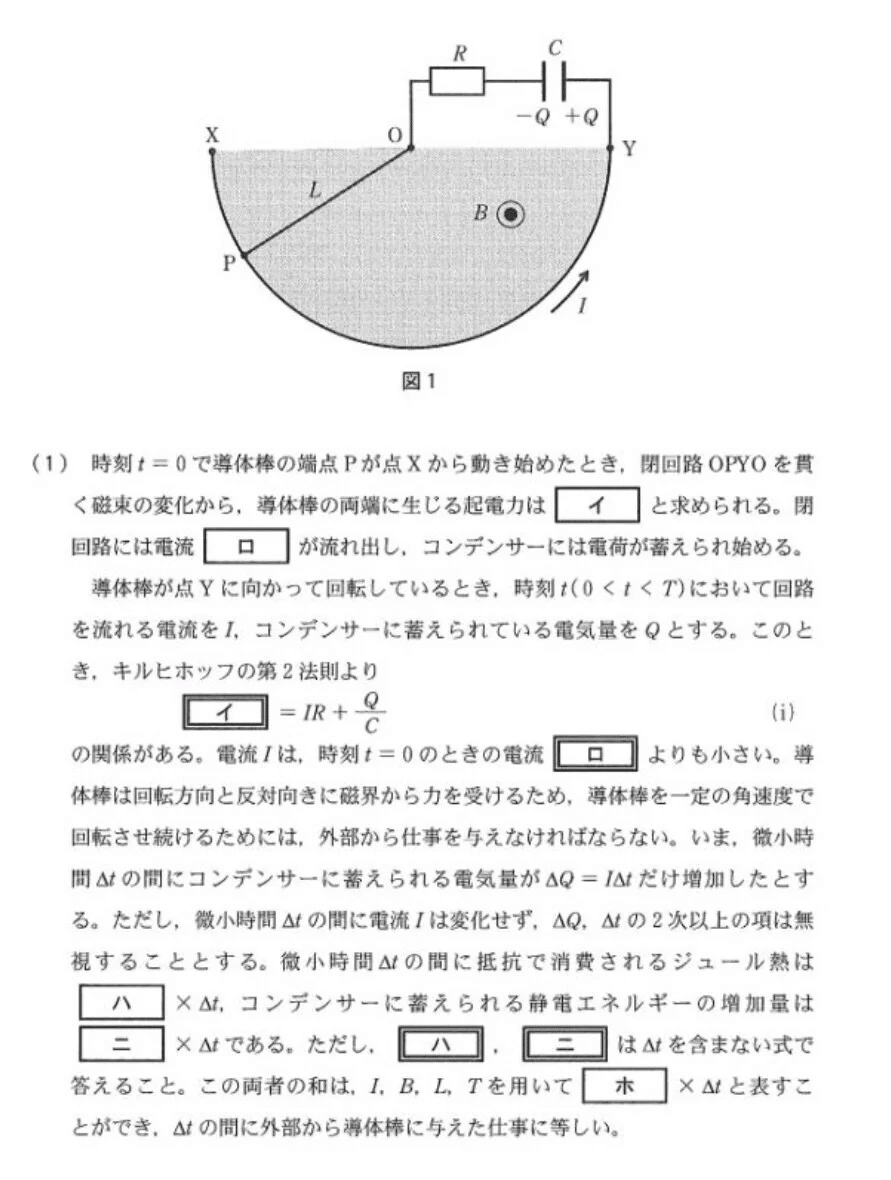


【解答】
(1) やや易
(イ)
<答1>
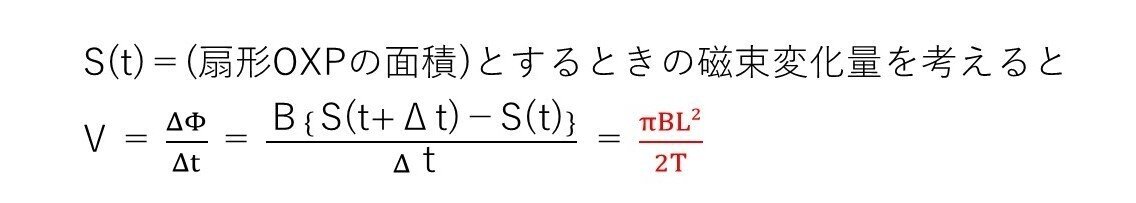
<答2>

<分析>
「導体棒の電子が反時計回りに動く=電流が時計回りに流れる」と解釈します。
フレミング左手の法則を用いると、電子が導体棒のどちら側に移動するかわかるでしょう🤔
そのうえで、-→+の向きに起電力が発生すると考えればいいのです☝
(ロ) 易

(ハ),(二) やや易~標準

<分析>
(電流)=(単位時間あたりに流れる電荷量)が理解できていればできます。
この考え方は、何気に化学の電気分解でも登場しますよね😳
(ホ) やや易~標準
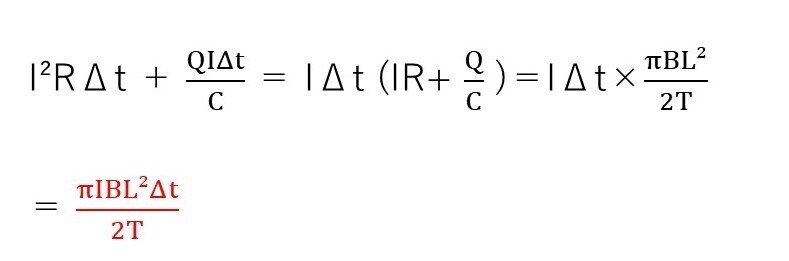
<分析>
前問ができれば、簡単な式整理でできます。
(2)
(へ) 易

(ト) やや易

(問1) やや易~標準
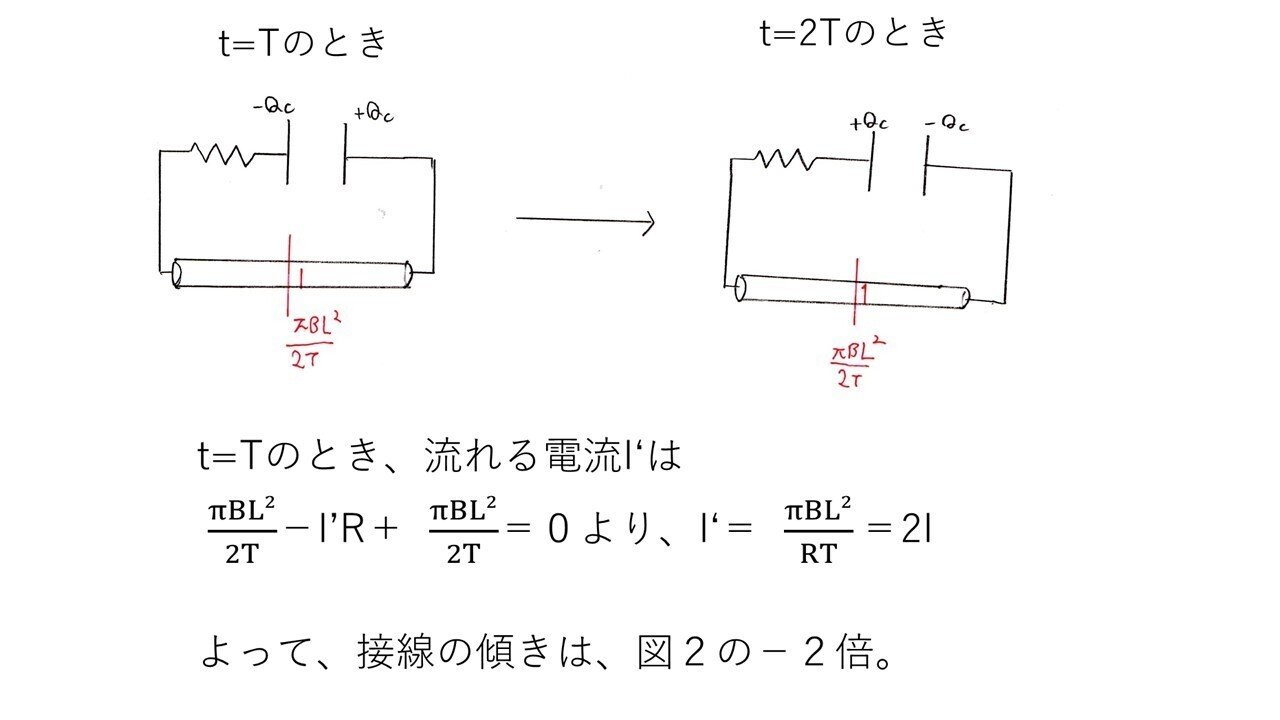
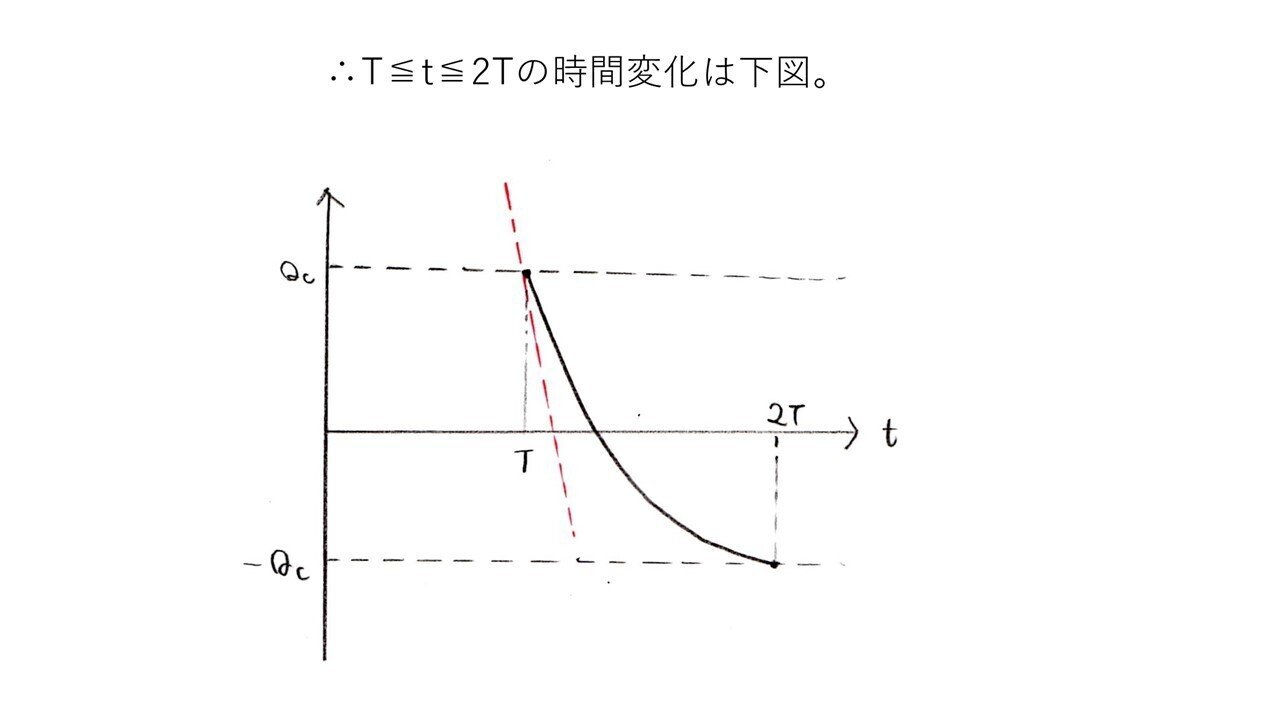
<分析>
図2と同様のグラフをT≦t≦2Tでも描けばいいのかな?という推測はつくでしょう🤔
実際、t=T直後の回路において、キルヒホッフの法則を立式すれば導出できます。
(3)
(チ) 標準
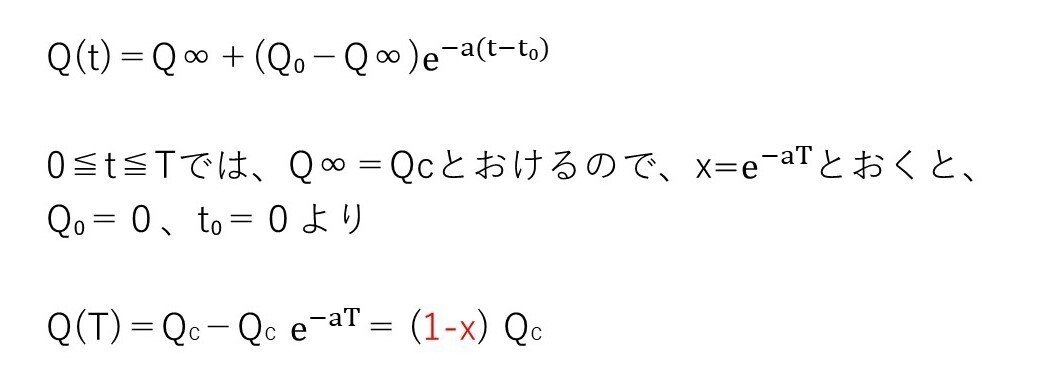
<分析>
「Q∞,Q₀,t₀が各状態で何を表すのか」さえ把握すれば、誘導に従えばOKな問題です。
(リ) やや難
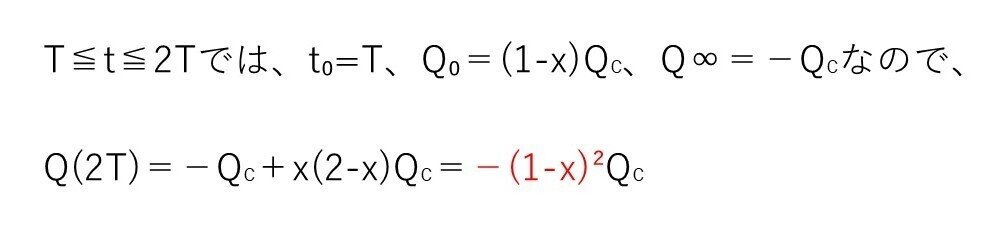
<分析>
やることは(チ)と同じですが、前問の正解が前提となるので、ここから少し難度が上がりますね。
(ヌ) やや難
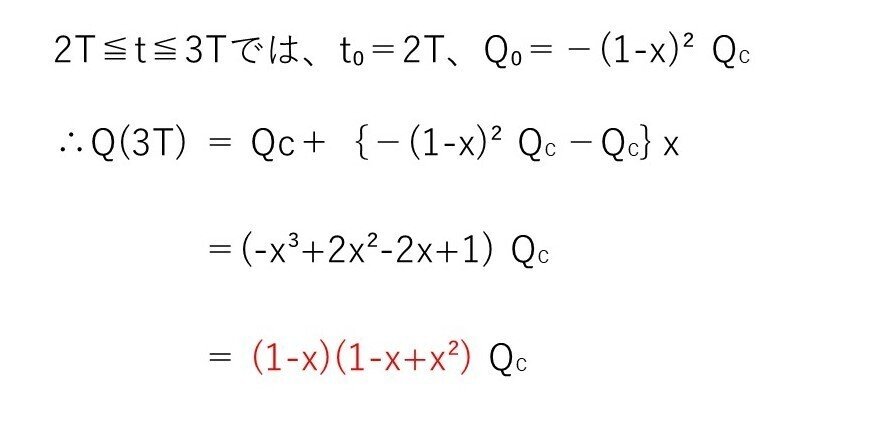
<分析>
(リ)と同様です。
(問2) やや難

<分析>
これも(3)の大筋を理解していればできる問題です。e^x=2.6が出たところで、eの近似値を使うとx<1が言えます。
<感想>
(2)以降は電源の向きを一定時間ごとにコロコロ変えたときのコンデンサー電気量の動きをみる問題で、数式を用いた考察力が問われます。
個人的には第2問の後半が今年の最難問ですが、コンデンサーの理解を深めるには良い問題と思います。
第3問
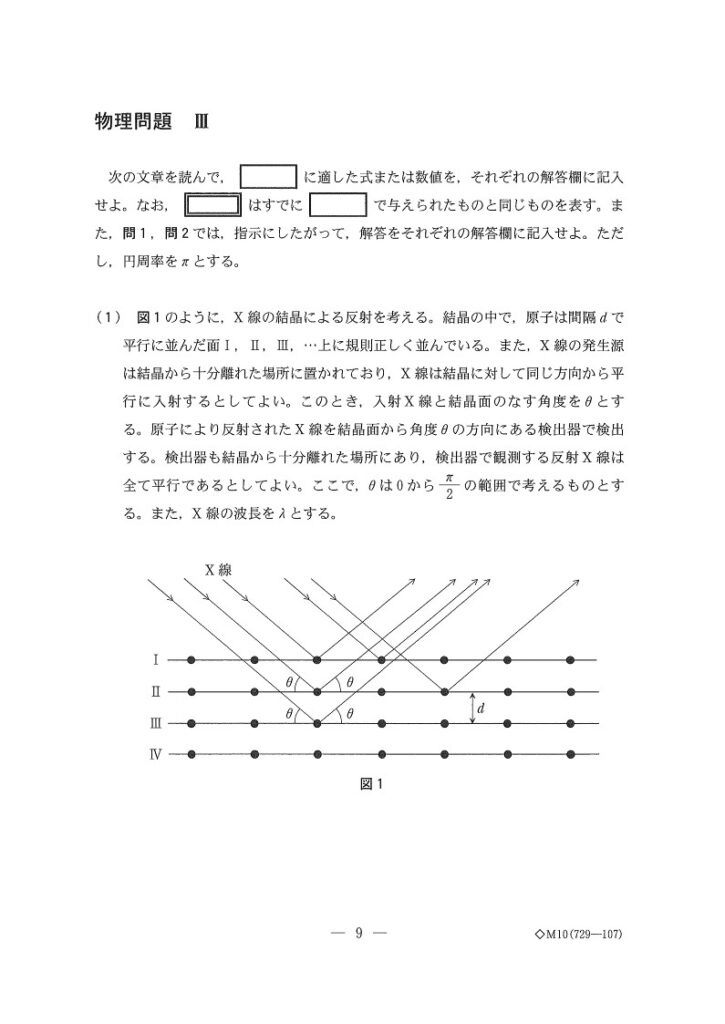




【解答】
(1)
(あ),(い) 易
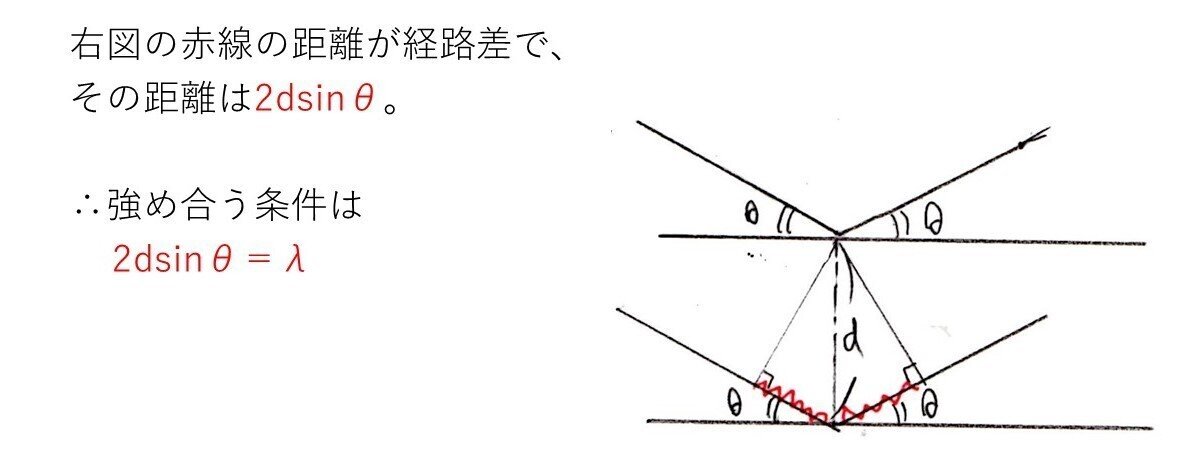
<分析>
経路差の超基本問題。正答必須ですね~💦
(2)
(う),(え) 易
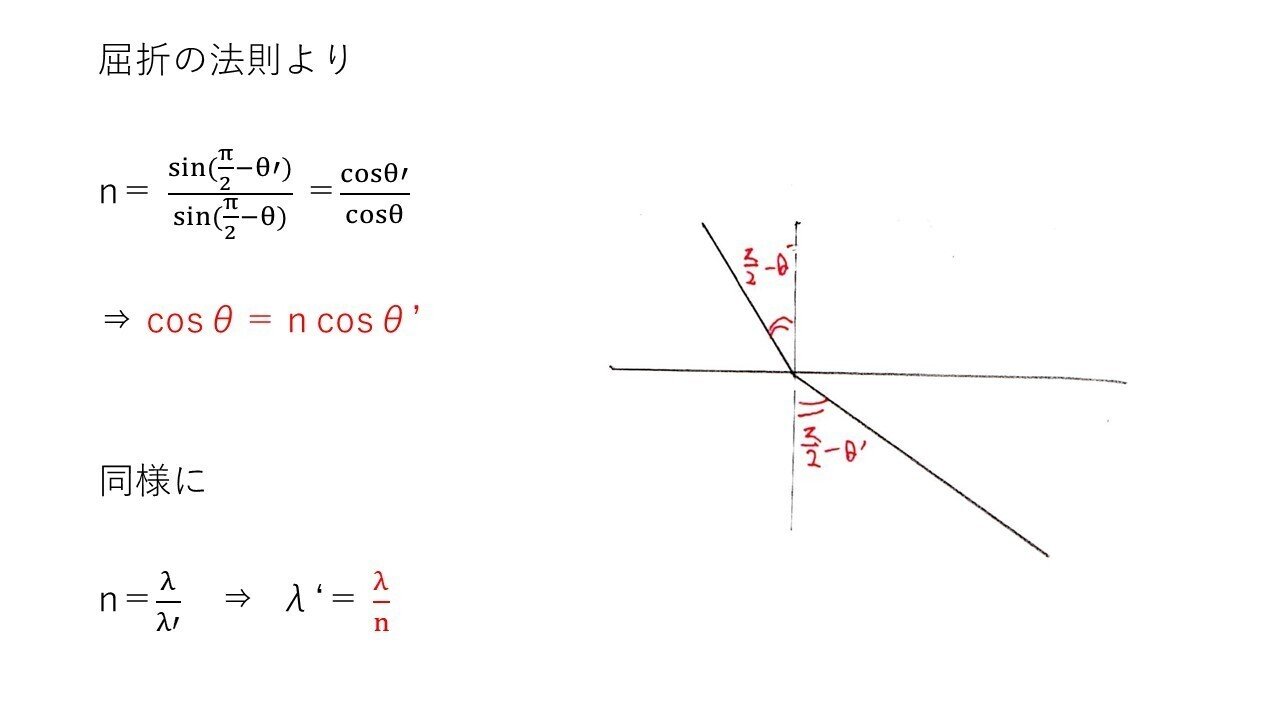
<分析>
屈折の法則を使う基本問題。これも全然取れるでしょう☝
(お) やや易

<分析>
経路差を位相に変換するだけの問題です。「1波長=位相差2π」は大丈夫ですか??
(か) やや易~標準

<分析>
「反射時に位相がπずれる条件」についてはよく認知しておきましょう。忘れた頃に出題されますので。
(3)
(き) 易~やや易

<分析>
エネルギー保存則で難なく答えられます。また、本問ではド・ブロイ波長が(3)の最初で与えられている分、受験生に対する配慮が感じられます。
ただ、ド・ブロイ波長はきちんと覚えておきましょう!!2021年阪大で、ド・ブロイ波長を知らないと5連続雪崩失点する問題があったのでね🧐
(問1) 標準

<分析>
ここも「1波長=位相差2π」を用いて、最後に近似式を利用すれば解けるでしょう!
(問2)
(ⅰ) やや難

<分析>
(問1)の正解が前提。処理はやや煩雑ですが、v₀の数値が与えられていないことから、v₀を消去すればいいことは推測できるでしょう。
(ⅱ) やや難

<分析>
(ⅰ)ができれば楽勝ですね☝
<感想>
(1)(2)はただの屈折波の問題です🌊
(カ)は意識すべきポイントがありますが、確保したいです✊
(3)は目新しい問題ですが、実は2017年頃?の慈恵医大に類題が出ています。参考に見ておくと良いでしょう。
総括
全問において、どれも後半になるまで難しい問題はないですね。
よって
苦手を残さずきちんと勉強していれば
7割までは容易に取れた
のではないでしょうか??
合格点は
非医:60~65%
医:80%
程度でしょうか。今年は高いですね~💦
医志望なら後半の問題にもある程度手をつけたいところ。取るとすれば第1問or第3問でしょう。
最後に、再度公式ラインの紹介をします。
私の公式LINEでは、無料相談を随時受け付けております。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってみてください✊
【⬇️公式LINE登録はこちら⬇️】





