
受験生の皆さん、こんにちは。
東大合格ビジネスマンのワタシですm(_ _)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ 3大基礎力重視の裏ワザ勉強法
に関する様々な情報を発信しております📢
私の公式LINEでは、無料相談を随時受け付けております。
公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってください✊
私も苦手科目は先生に頼りました。
また、LINE登録していただいた方には
無料プレゼント(1年で偏差値70出す画期的勉強法)
を贈呈します🎁
【⬇️公式LINE登録はこちら⬇️】

2021年入試、旧帝大の第7弾は
「東京大学」です。
当ブログの解説記事は
読者が必死に3年間努力すれば
東大(理三以外)・京大(医以外)・九大医
レベルに80%以上の確率で合格できる
ことを目的に作成しています
市販の問題集のように、解法を丁寧に示すだけではありません!多角的なアプローチで問題を解きほぐしています✊
① 各問の難易度
② 他分野や一般常識との関連事項
③ 問題の躓きポイント
④ 極力曖昧な表現をしない説明
を示しています。
イマイチ成績が突き抜けられない受験生に貴重な情報が提供できればと思いますm(__)m
東大理系数学の特徴
東京大学の理系数学は全6問で制限時間は150分です。
例年
第1問は易しめな傾向があり
やや易〜標準が3〜4問
やや難〜難が2〜3問という印象
ですね🤥
今年は果たしてどんなセットだったのか?
第1問

【解答】
(1) 易~やや易

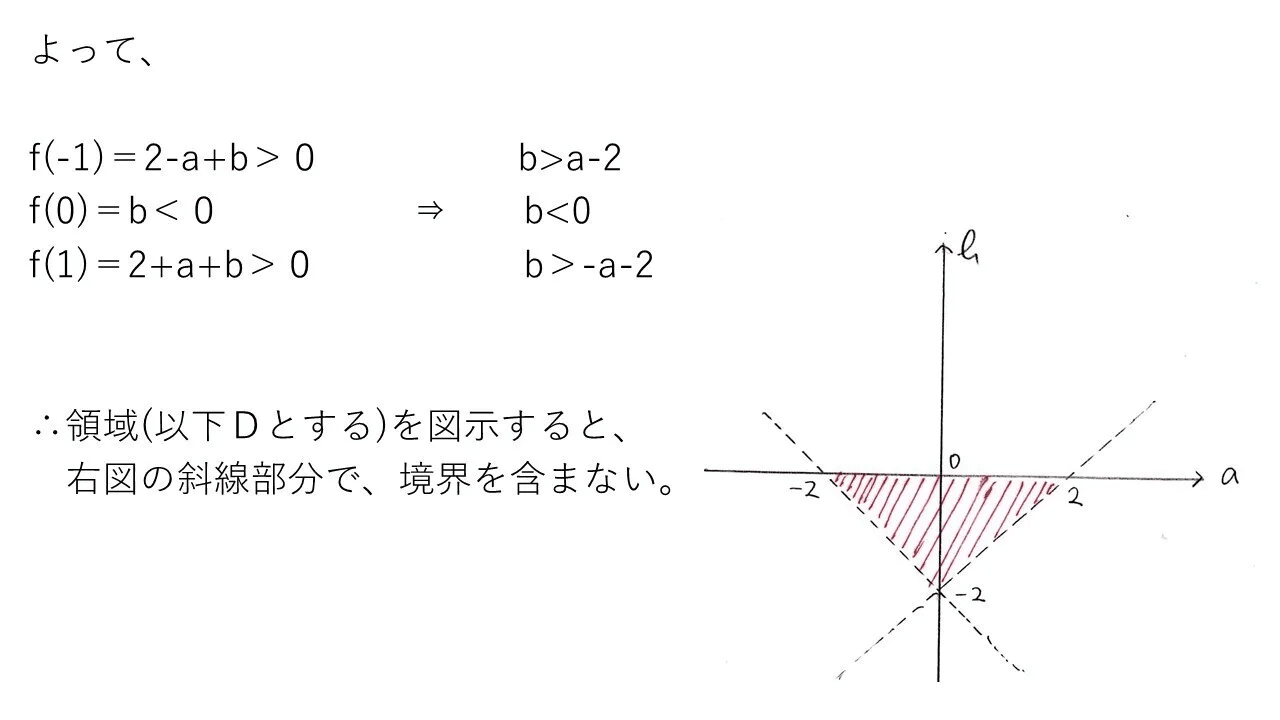
<分析>
共通テストレベルですね(笑)
2曲線f(x),g(x)の交点 ⇒ f(x)-g(x)=0の形の2次方程式を作り、条件を満たすように判別式,軸,値の正負を設定すればできます💡
(2) やや難
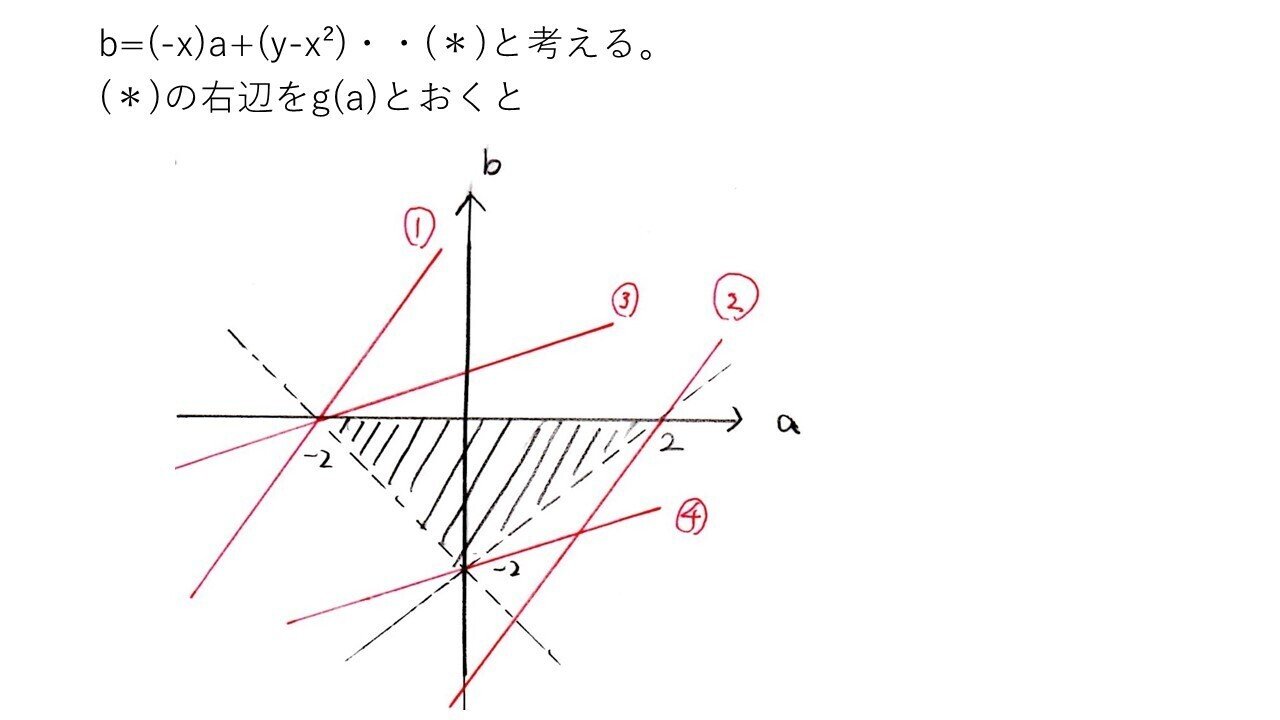


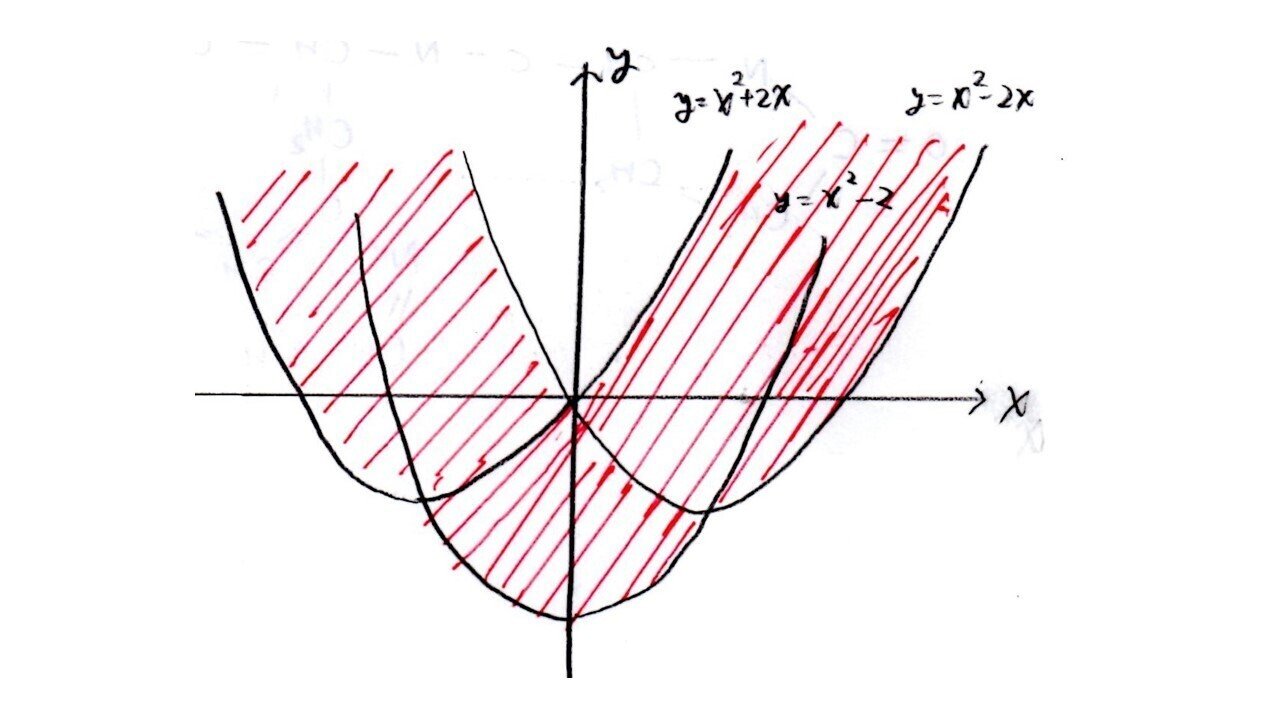
<分析>
y=x²+ax+bで2変数a,bを動かして求めるのは困難です。
では、どう考えるかですが「そもそも、何のために(1)があるのか?」「(1)で出した(a,b)の領域をどう使うのか?」を考えます。
C:y=x²+ax+bにおいて(x,y)を定数、(a,b)を変数とみなして、b=(-x)a+(y-x²)・・(*)とおくとき、領域D内の点(a,b)が直線(*)上に存在するためのx,yの条件を求めるといいでしょう。
<感想>
(1)は落とすと論外、(2)はやや難レベル。やや難の定石解法を学習できる良問です。
(2)は(1)で出たab平面の領域を使えないかを考えたいですね🧐
b=(-x)a+(y-x²)と変形してしまえば、「軌跡と領域」でよくみる典型パターン(「線形計画法」と呼ぶ)に帰着します。(1)でab平面の領域が出ているので、xとyを定数、aとbを変数とし、見方を変えて式変形できるかがkey🔑でした。
第2問

【解答】
(1) やや易
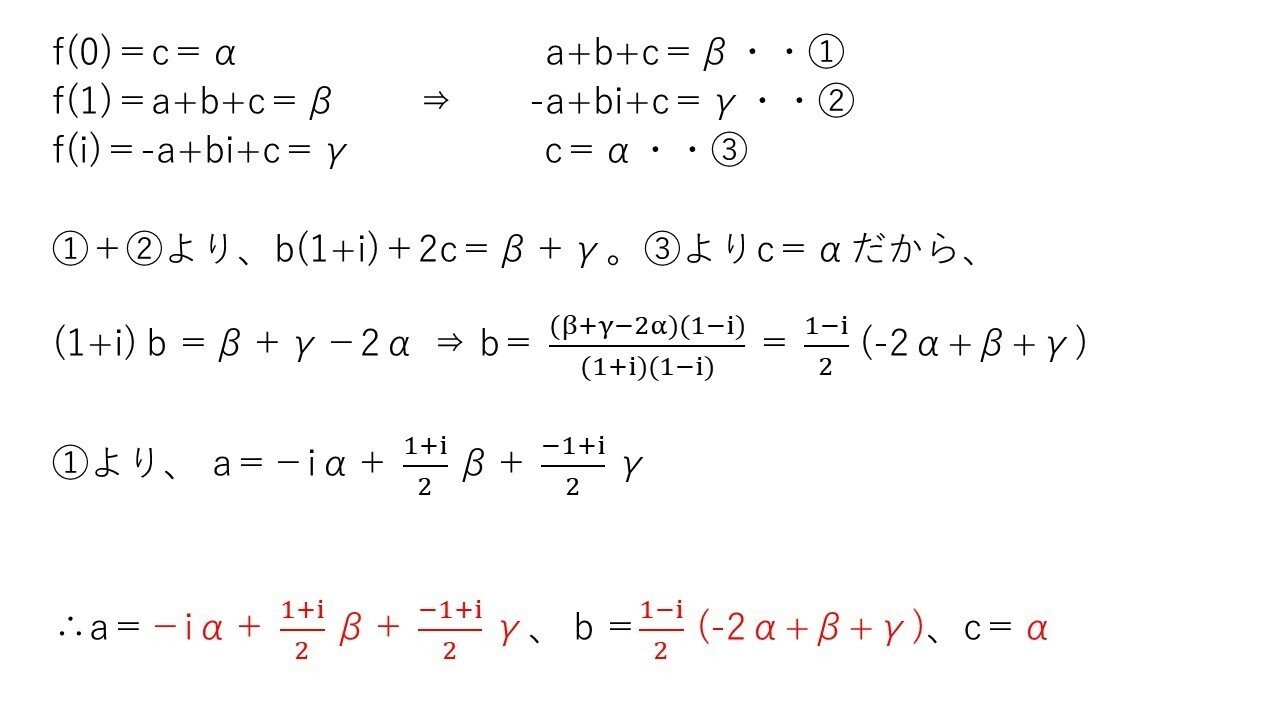
<分析>
求めるのはa,b,cの3つ。f(0),f(1),f(i)は未知数3つの連立方程式なので、答は簡単に出ます。計算は少し煩雑。
2) やや難~難
<分析>
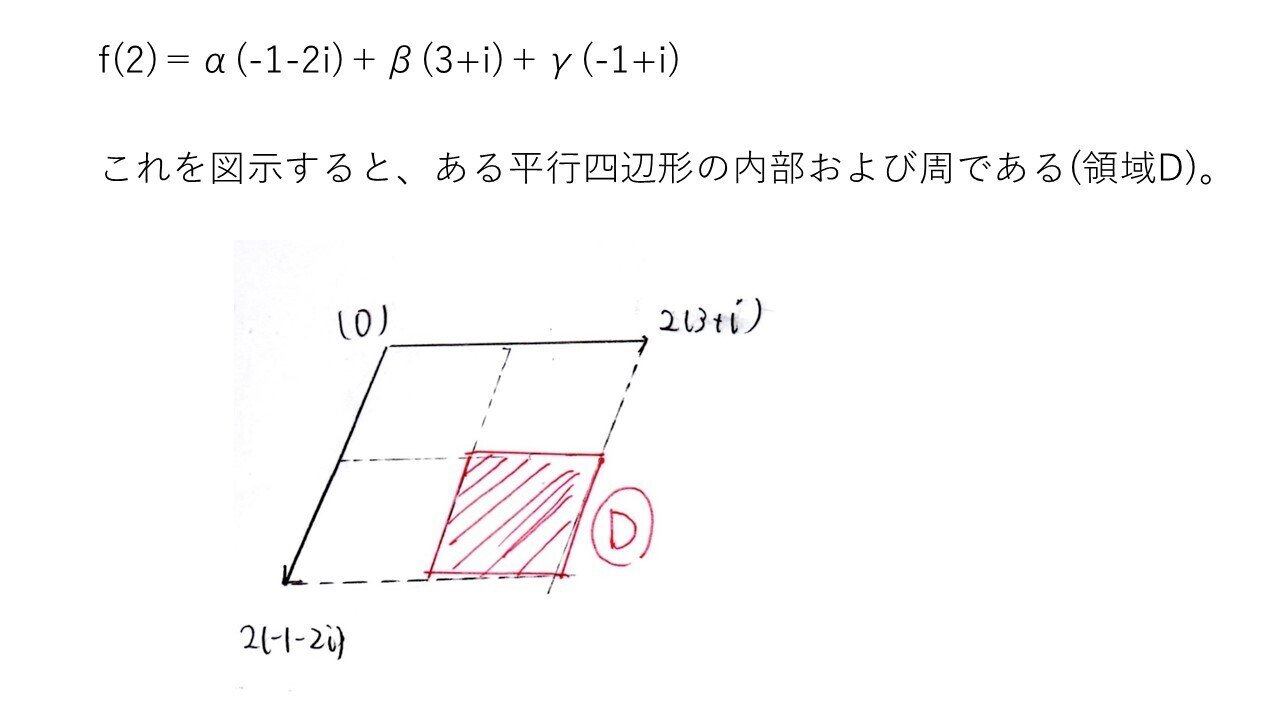
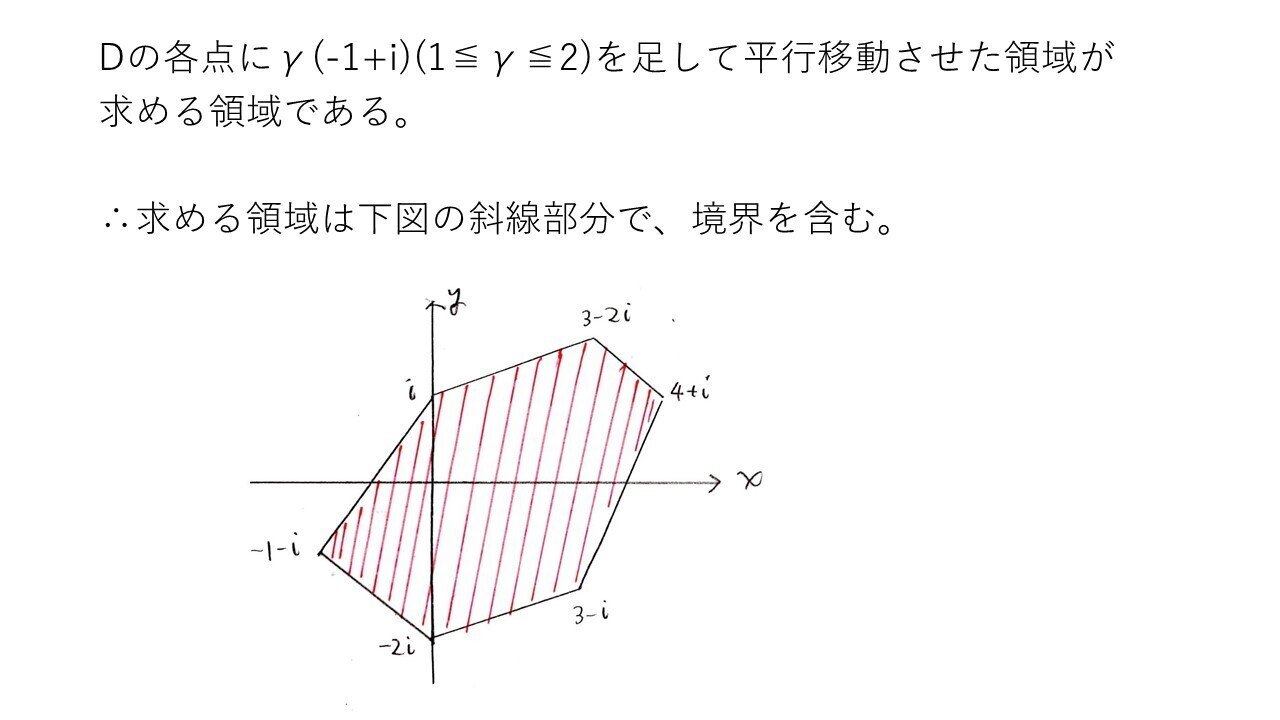
複素数平面をベクトル風に考える問題です。つまり、本問では、f(2)=α(-1-2i)+β(3+i)+γ(-1+i)をα(-1,-2)+β(3,1)+γ(-1,1)と考えるということです🤔
この手の問題は受験生的には盲点だったのでは??しかし、実は「やさしい理系数学の例題」にもあったし、「東大プレの過去問(2020年頃?)」にもありました💡
手が出なかった人は、次に類題ができるように、解法をよく復習しておきましょう。
<感想>
(1)は虚数 i を含むただの計算なので、正解しましょう💡
(2)は未経験だと難しいですね。理Ⅰ,Ⅱなら捨て問でも仕方なく、理Ⅲでも第1問が完答できていれば(2)は落としても問題ないて感じです。
(2)は「複素数平面をベクトル風に捉える問題を解いた経験」の有無で差が付いたと思われます😅w=αz₁+βz₂+γz₃で、αz₁+βz₂が四角形(平行四辺形)を表すことに気付き、その四角形をさらにz₃方向にγ倍平行移動させることを考えたいですね。
第3問

【解答】
(1) 易~やや易

<分析>
接線の求め方は超基本。あとは、商の微分ができて、3次方程式=0がx=1で重解をもつことがわかればできます。
(2) 標準~やや難

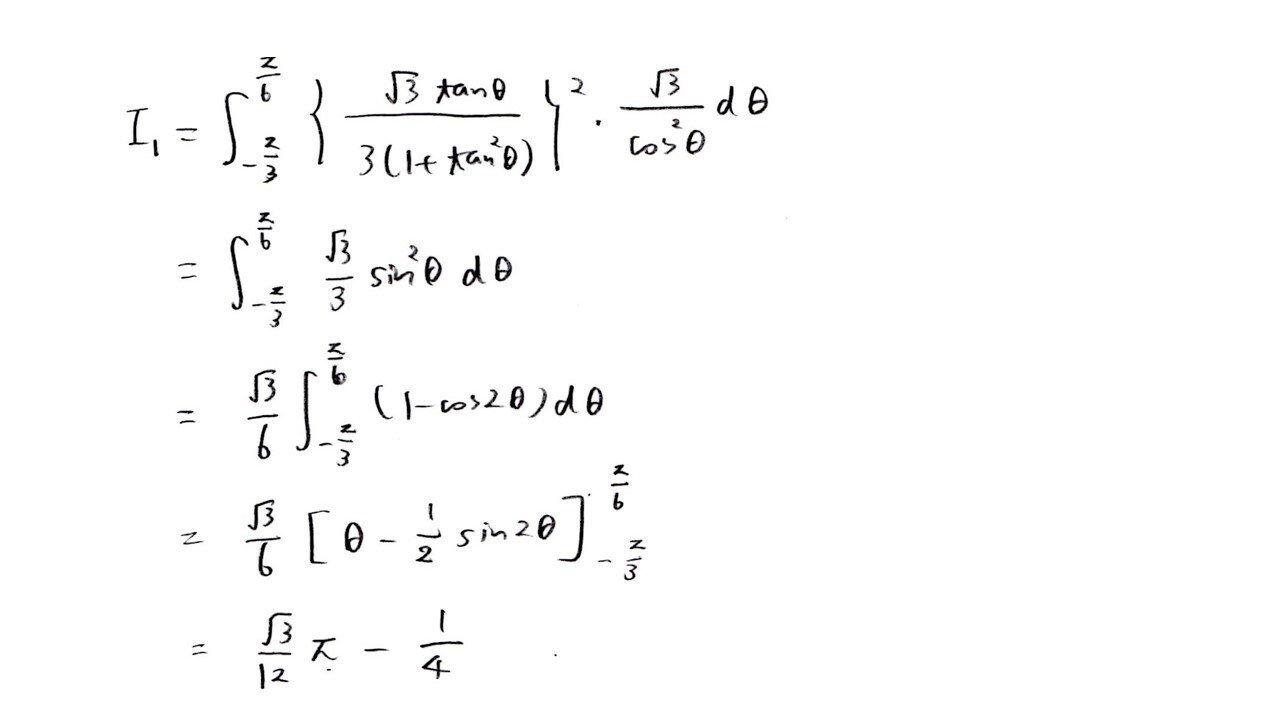
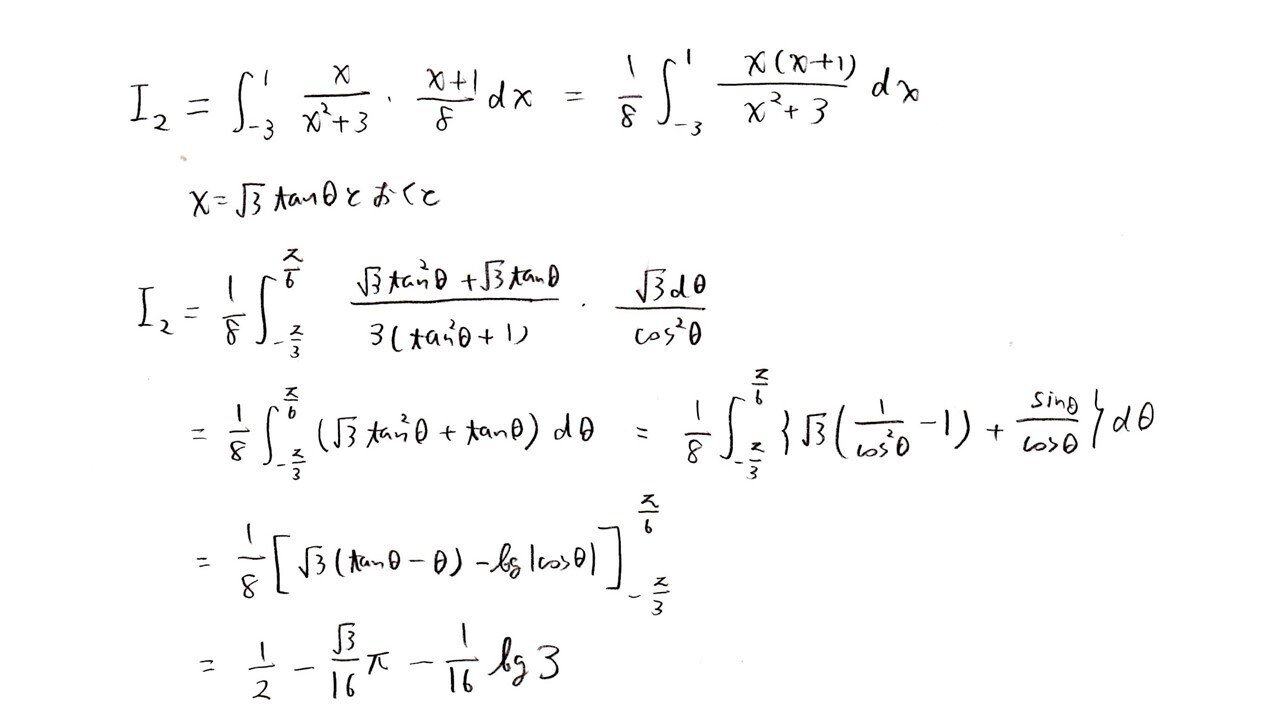
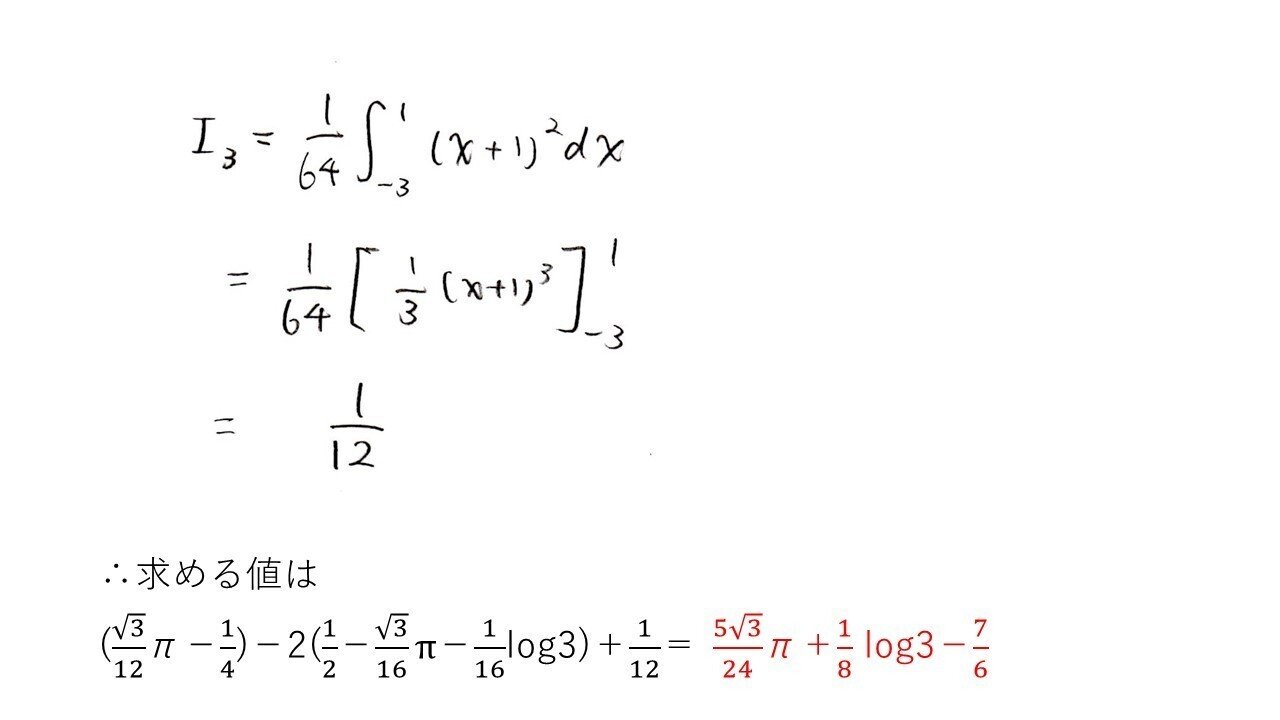
<分析>
1つ1つは基本の組合せですが、計算処理が大変ですね。
分母がx²+a²の形になっているときにx=atanθとおくのは定石ですよ、大丈夫ですか?一番難しい部分は「√3tan²θ+tanθの積分」ではないでしょうか。
<感想>
(1)は典型問題ですが、f(x)-g(x)=0の因数が(x-1)²である点に着目したかったですね👀
(2)は計算が煩雑で時間を食うし、答えも汚い。完答難易度は低めだけど体力勝負でなところがあり、数学というより計算問題では??という印象でしたね😂
第4問

【解答】
(1) 標準

<分析>
「4の倍数とわかっているK-LとA-BをKA=LBから炙り出せないか?」と考えると、上記のような解法がイメージできるのではないでしょうか🤔❓
(2) 難
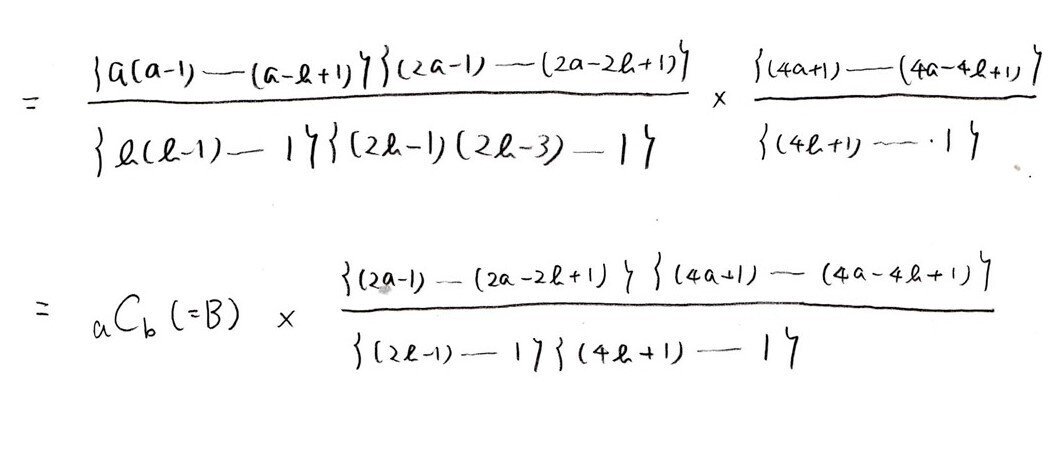
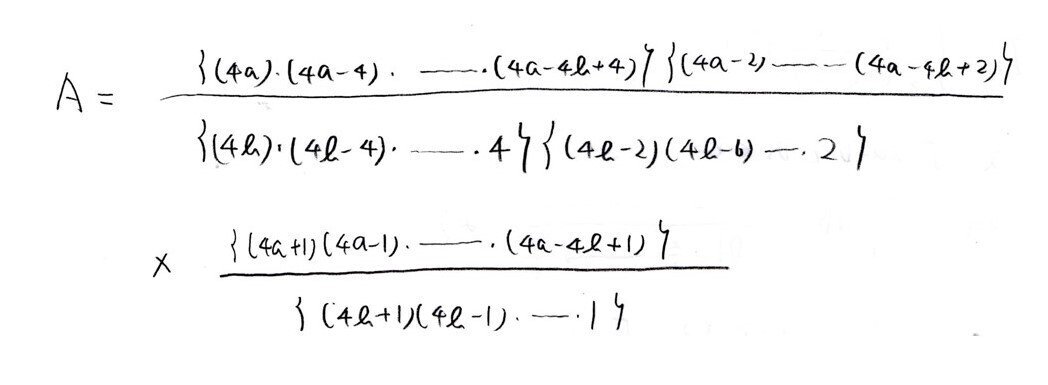
<分析>
Aの分母,分子に現れる整数を「4の倍数、4で割って2余る数、奇数に分解」して考えます。
先行きが見えないときは、ごく小さな値で試してみます👀
すると、AとBがともに(2の累乗)×(奇数)の形で表せて、B/A = L/K≠偶数を示せばよいのでは?と推測できます☝️
しかし、そこからが難しいですね💧二項係数のよくする変形aCb=a!/b!(a-b)!をしても何も見えてこない。
捨て問でも仕方ないでしょう🤥
(3) 難

<分析>
(2)で正しい変形ができていないと着手できないので、これも難しいです。
仮にクリアできれば、(1)の結果を利用して解決ですが。
(4) やや易

<分析>
(3)の結果を使うのはミエミエでしょう👀
4×505+1=2021,4×9+1=37より、当初a=505,b=9として値を下げていくとよいでしょう💡
<感想>
(2),(3)は捨て問でも仕方ないですね~。
(2)(3)が難しすぎるために気分が萎えてしまい、(4)も捨てた受験生は多そうです。(4)は一読すれば(3)を使うのは自明なんだけど・・・こういう失点は勿体ないよね😱
本問からは東大からのメッセージを感じますね。「(2)(3)は手も足も出んやろうけど、後に簡単な(4)を配置したからそれは諦めずに取れ!」みたいな(笑)
第5問

【解答】
(1) 標準
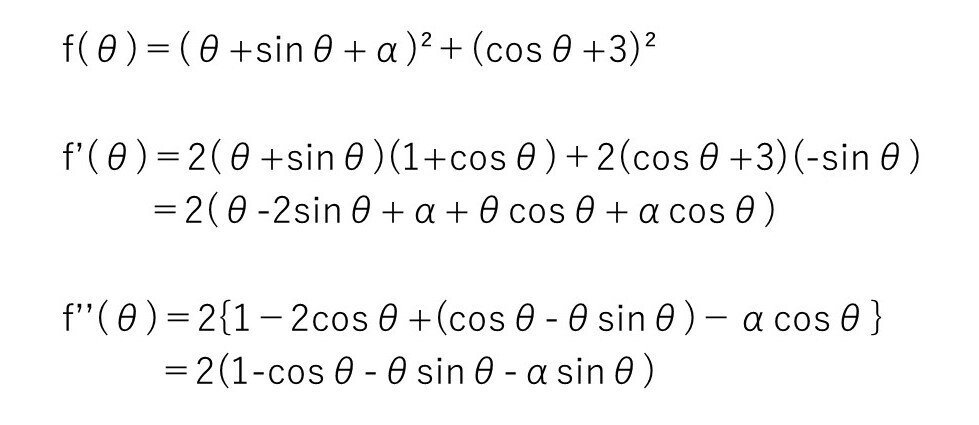
この時点ではf”(0)=0、f”(π)=4はわかるけど、その間の増減がはっきりしない!以後どうするか?
<解法1>

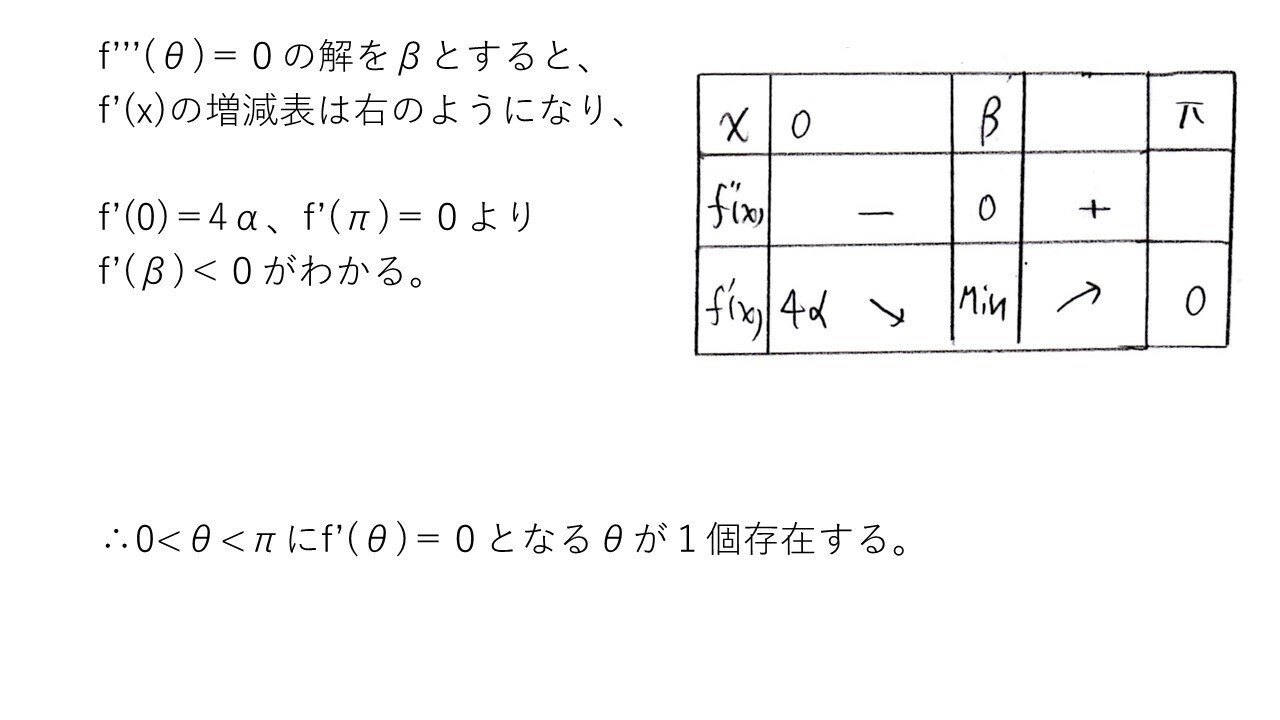
<解法2>


<分析>
思い切って3回微分すれば解決できる問題です☝️
まあ、2回微分でも<解法2>のように解決できますが。
しかし、2回微分まではよくするけど、3回微分ってほぼしないし、する気が起きないのも無理はありません😅
f”(θ)の形を見て、「θsinθを微分すればsinθが出ることと(cosθ)’=-sinθに着目して、うまくsinθが消えるのでは?」と思えれば、微分する気になったかも?
(2) 標準
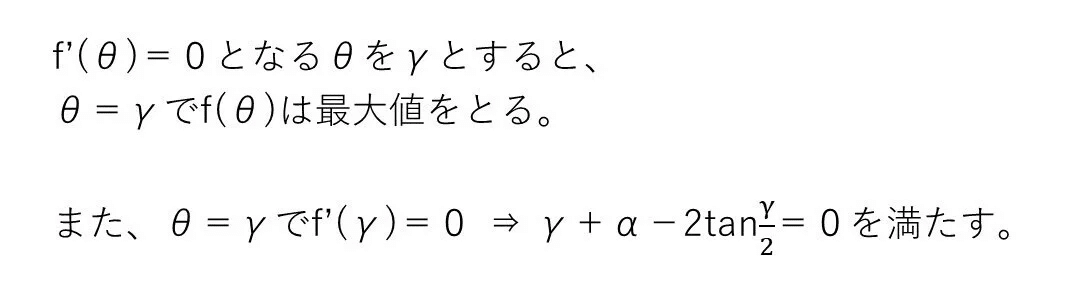
<解法1>

<解法2>

<分析>
(1)ができればおまけです😄
f'(x)の正負に着目したり、定数分離したりでできますが、どちらもお馴染みの解法ですよね。
<感想>
(1)で3回微分する前に諦めた受験生が割といそうですね。まあ滅多にしないからね。
ただ、「今まで3回微分した経験ない→した経験がないから諦める」といった、パターン暗記や固定観念に囚われた受験生を跳ね返すという意味では良問ですね。
なお、(2)はおまけで、第5問は今年のセットでは簡単な方。ほぼ0点or満点に二極化する大問で、混ぜるな危険ならぬ「落とすな危険🚫」問題です。
理Ⅲでこれ落としたら致命傷でしょうね・・ひぇ~😅
第6問

【解答】
(1) 易

<分析>
ただの恒等式の問題。高1でも解けます(笑)
(2) 標準

<分析>
(1)でqr=cを使ってないことに着目すると、(2)で使うのかな〜?と思ってほしいところですね🤔
qr=cの式をpのみで表した後は、結果式より逆算して考えます。{p²-(a²+1)}を因数にもつことを念頭に置いて変形するとよいでしょう。
(3) やや難


<分析>
(1),(2)であった、p≠0の条件が(3)ではないことに注意しましょう!
p≠0のときはpを含む部分とaを含む部分がすべて正になることを意識すれば解けます。
p=0のときは結局解なしなんですが、示し忘れていると減点されます。
<感想>
例年の第6問は難問率が高いことが多いけど・・・今年はそうでもないですね🙄
しかし、隠れた罠が存在するため、満点は逃しやすいでしょう。
(2)は計算がやや煩雑ですが、qr=cを使っていない点に着目できれば取れたはず。(3)はp=0の場合を見落としやすく注意🔰
ただし、最終問であることを考えると、p=0以外を取れれば上出来でしょう。
総括
第5問を除く大問は、基礎力さえあれば(1)は取れるので、(1)はマストで取りましょう✊
これで40/120点は可能。40〜50点なら昔の東大理系より取りやすくなってます。
あとは、どこで積み上げるかですが
まず
捨て問にする候補は最難問の第4問(2)(3)
でしょう。
第2問(2)もベクトルの性質を深く理解していないと厳しいかなと。
以上より、key問題は「第3問(2)の計算」「第5問」「第6問(2)以降」となってきます🔑
特に
第5問はall or nothingな性質が強いので
特に理Ⅲ志望者は落としたくない
でしょう。
ボーダーは
理Ⅰ:50%
理Ⅱ:45%
理Ⅲ:65〜70%
程度ですかね~🙄
最後に、再度公式ラインの紹介をします。
私の公式LINEでは、無料相談を随時受け付けております。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってみてください✊
【⬇️公式LINE登録はこちら⬇️】






