
受験生の皆さん、こんにちは。
東大合格ビジネスマンのワタシですm(_ _)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ 3大基礎力重視の裏ワザ勉強法
について、様々な情報を発信しております📢
私の公式LINEでは無料相談を随時受け付けております。公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってください✊
私も苦手科目は先生に頼りました。
また、LINE登録していただいた方には、無料プレゼント(1年で偏差値70出す画期的勉強法)を贈呈します🎁
無料相談もどしどし受け付けております✊
【⬇️公式LINE登録はこちら⬇️】

2021年入試、旧帝大の第2弾は
「東北大学」です。
当ブログの解説記事は、長期的な目線で成績を飛躍的に伸ばし、継続性・応用性のあるスキルを身に付けていただく記事です。
読者が必死に3年間努力すれば
東大(理三以外)・京大(医以外)・九大医
レベルに80%以上の確率で合格できる
ことを目的に作成しています
市販の問題集のように、解法を丁寧に示すだけではありません!
多角的なアプローチで、適所で関連事項や模範解答ではない解説を投入し、必要以上に問題を解きほぐしています✊
① 各問の難易度
② 他分野や一般常識との関連事項
③ 問題の躓きポイント
④ 極力曖昧な表現をしない説明
を示しています。
イマイチ成績が突き抜けられない受験生に貴重な情報が提供できればと思いますm(__)m
東北大理系数学の特徴
東北大学の理系数学は全6問で制限時間は150分です。他の旧帝大では、大阪大学や九州大学が同じ150分で5問なので、阪大や九大より少しスピードが要求されますね🏃♂️
北海道大学よりは若干問題が難しく、
満点阻止系の難問も少しは存在する
という印象です🧐
問題を深く理解するためには
全統記述模試で偏差値55~60程度
は必要かと思います。
全統記述模試の難易度や受験者レベルについては、各自で確認されてくださいm(__)m
第1問
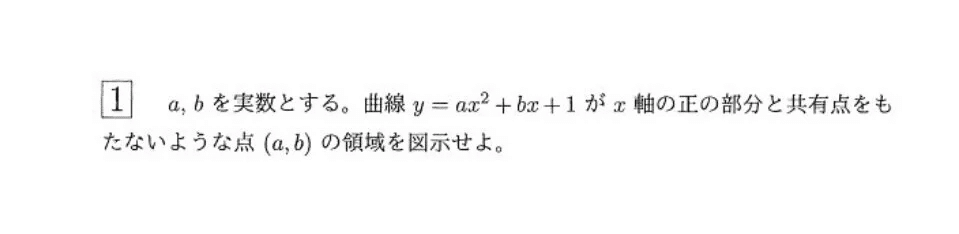
難易度:標準
【解答】
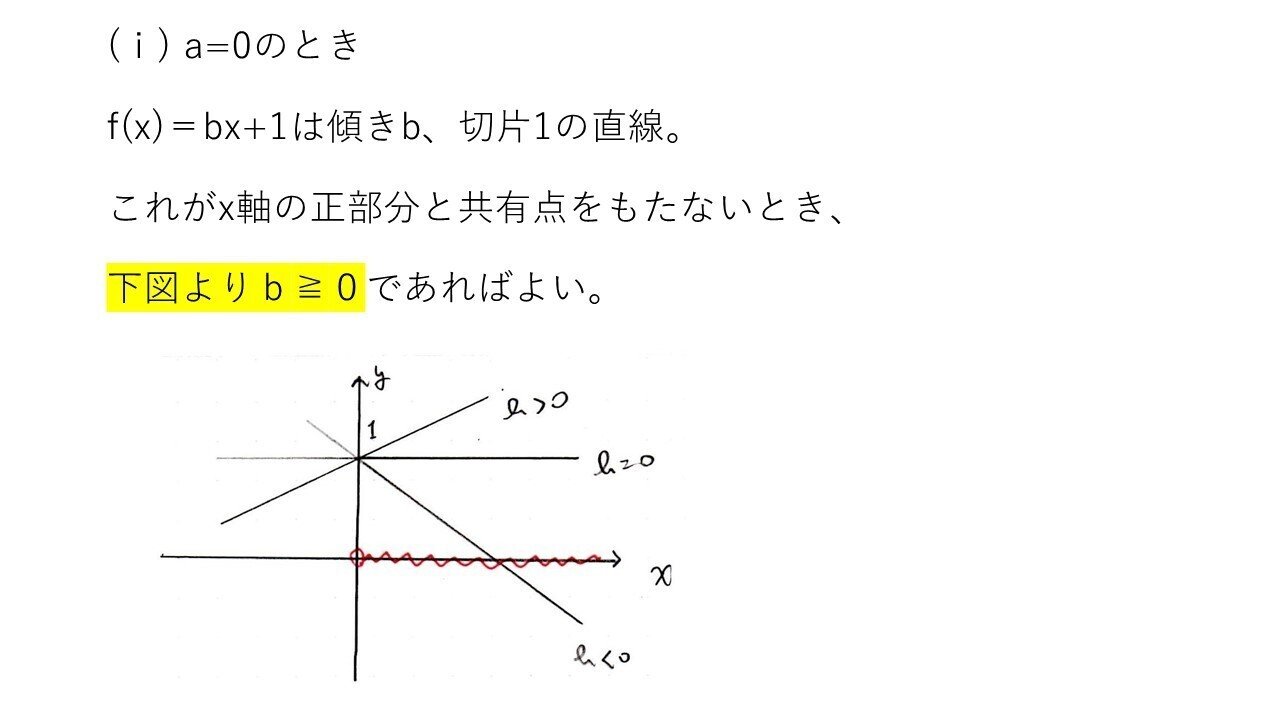
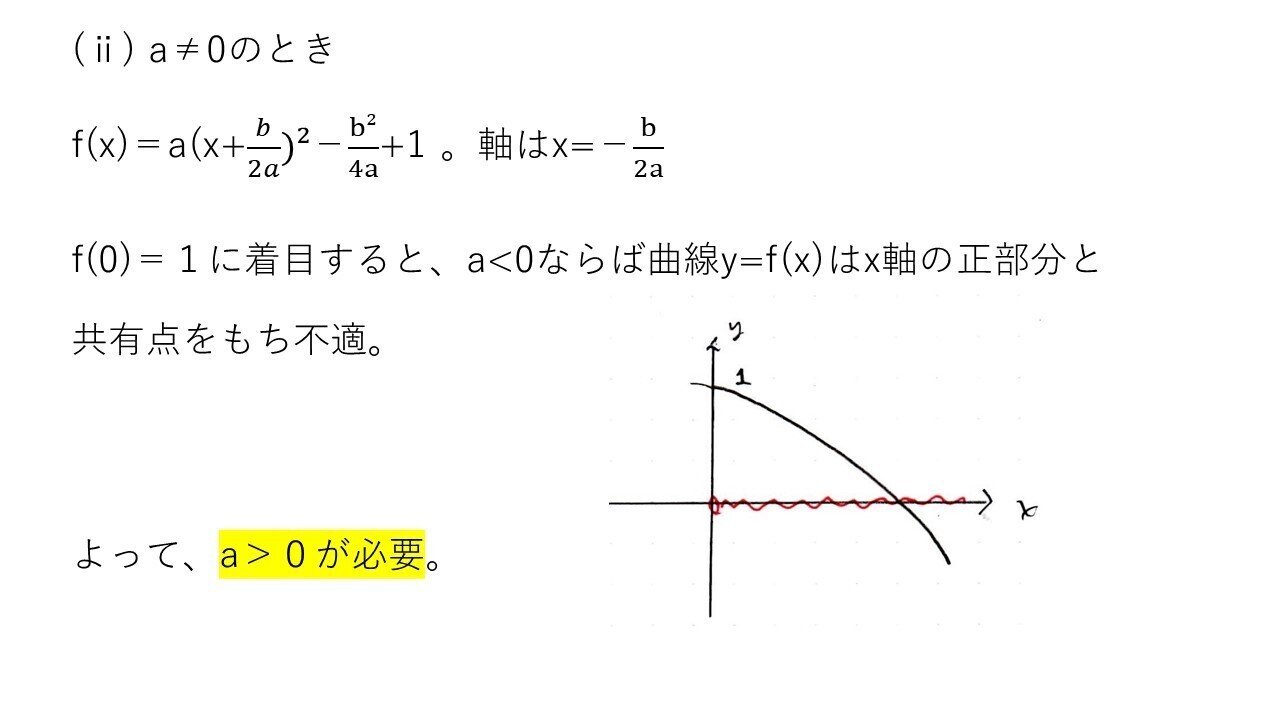
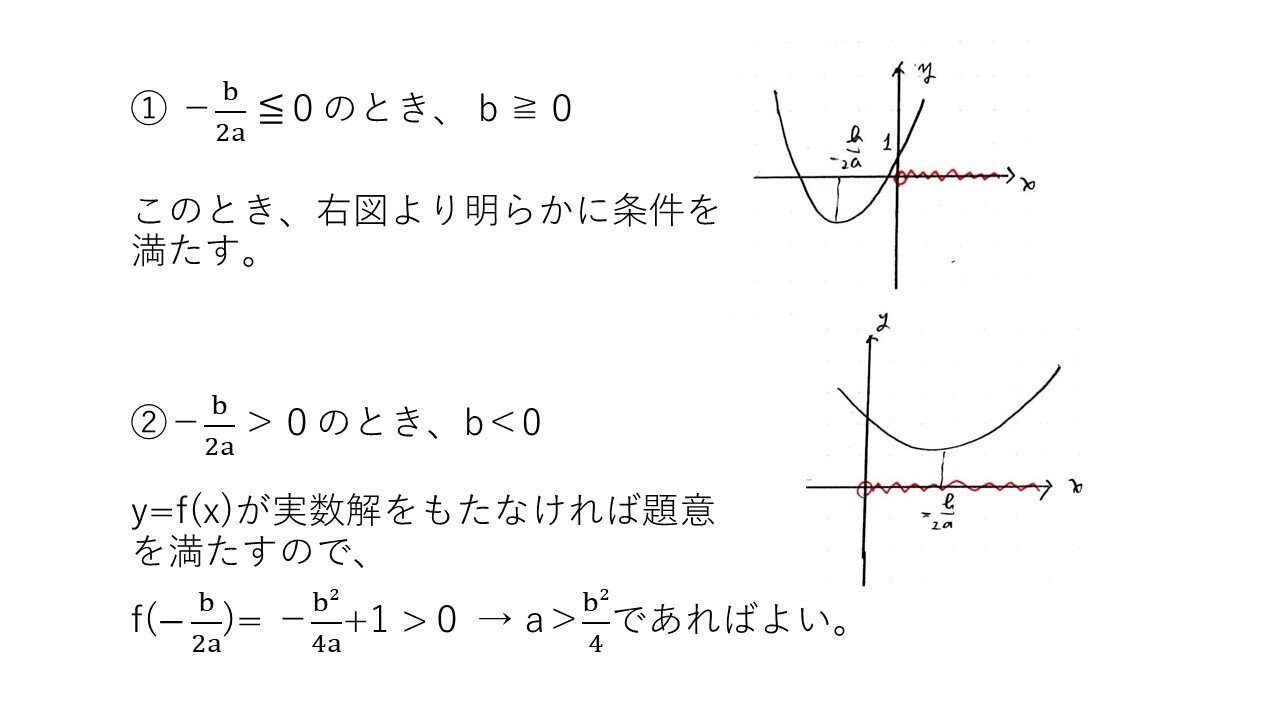
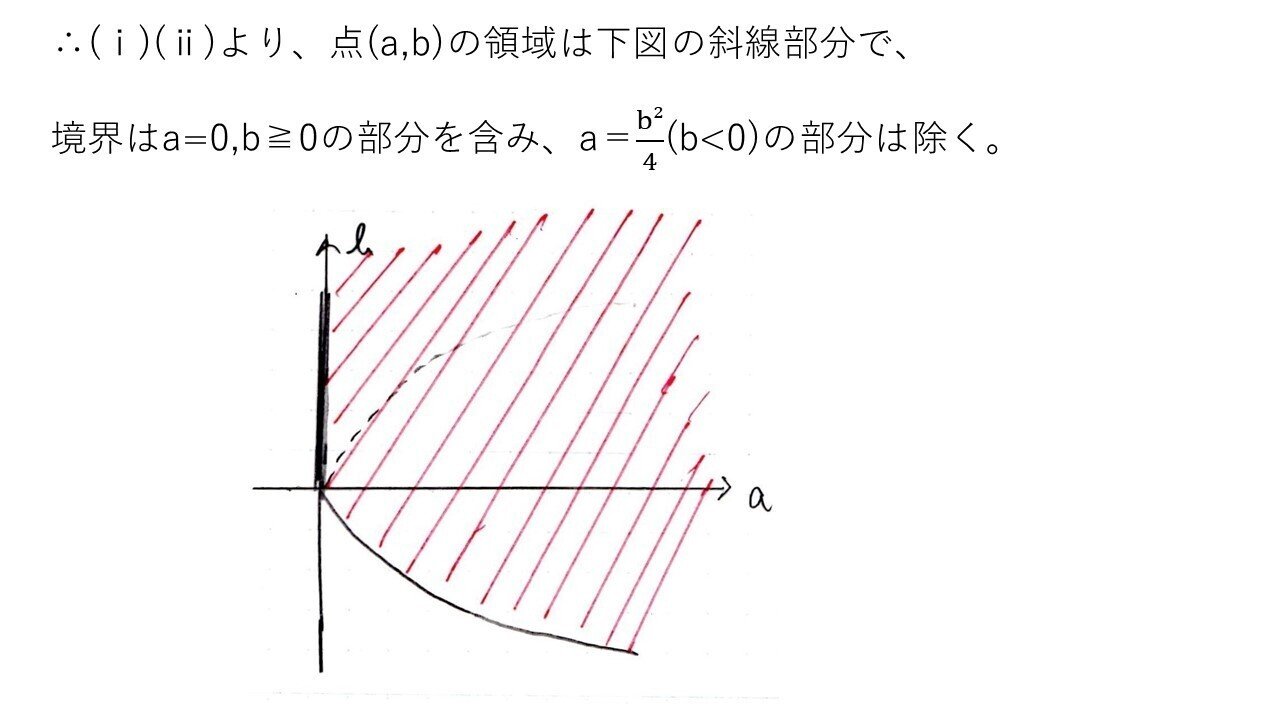
<分析>
2次の係数aに着目してa=0か否かで場合分けできたかがkeyでした🔑
あとは、標準的な2次関数の調査系問題ですね。演習を積めば問題なくできます。
第2問

【解答】
(1) やや易
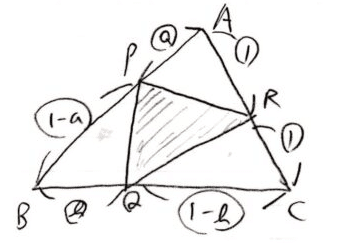

<分析>
△PQRの面積を直接求めるのは困難。△ABCから△APR,△BPQ,△CQRの分を引けばどうか?と発想したいところです🤔
確率でいうところの、余事象的な考え方ですね。
ちなみに、(1)が詰むと(2)(3)もできませんので、得点差がついた問題だったでしょう。
(2) 標準

<分析>
T/Sは2変数a,bの関数です!2変数関数では「一方を固定して他方を動かす」のが典型的解法です。
ここでは、T/S=f(a,b)とおき、まずbを固定してみましょう✊
(3) 標準

<分析>
(3)は(2)が出たら、サービス問題😂
T/Sの範囲が出たこと、S/Tが整数であることより、S/Tの値は3しかありえません✋あとは、p,qの式にして整理すると、pq-3p-3q+6=0の形が出ます。この因数分解はどこかで見覚えがあるでしょう👀
第3問

下図のように円周を8等分した点をA₁,A₂,・・・,A₈とする。
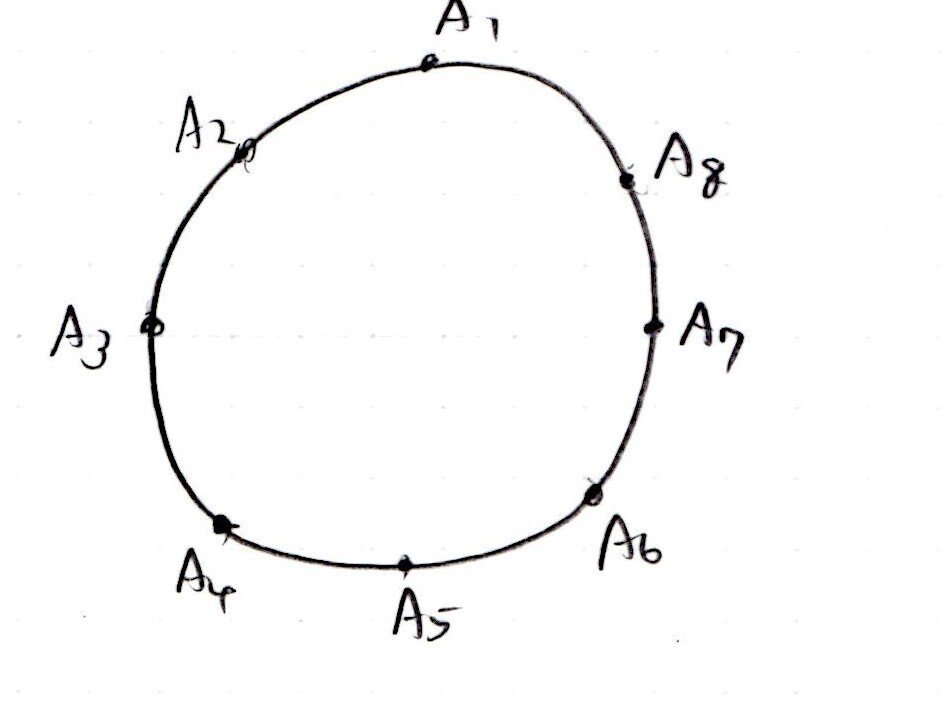
【解答】
(1) やや易

<分析>
正多角形は円に内接・・正多角形が出てきたら外接円の存在を意識しましょう✊
(1)は「円周角が90°になる⇒対辺は直径」の性質に気付くことがポイントでした。
(2) 標準~やや難

<分析>
「~でもない」ときたら、余事象的に考えることを意識しましょう✊
(2)は全三角形の個数から条件に該当しないものを引く方法で求めましたが・・・②で正三角形に言及したのは、もし正三角形が存在する場合に重複数えが生じるためです💦
(3) やや難

<分析>
四角形から三角形は2つできる(下図)ことに着目し、対角線が直径か否かで分類する方法を取りました。
しかし、丁寧な調査には粘り強さが求められますね💦(2)(3)では重複分を除く部分で出来不出来の差がついたでしょう。
第4問

【解答】
(1) やや易~標準


<分析>
①の3次方程式の解の1つがx=aと与えられているので、P,Qのx座標は2次方程式「x²+ax+a²-3」の2解だとわかるでしょう。
PQの中点のx座標はα+β/2で与えられることから、あとはα+βがわかれば解けます。
そこで用いる性質が「解と係数の関係」ですね!
(2) 標準


<分析>
軌跡の式を出すの自体は難しくないでしょう。問題はxの範囲ですね。
ここで「x³-3x-k=0が3つの実数解をもつkの条件」を考える必要があり、合否を分けたポイントだと思いました🤔
(3) 標準
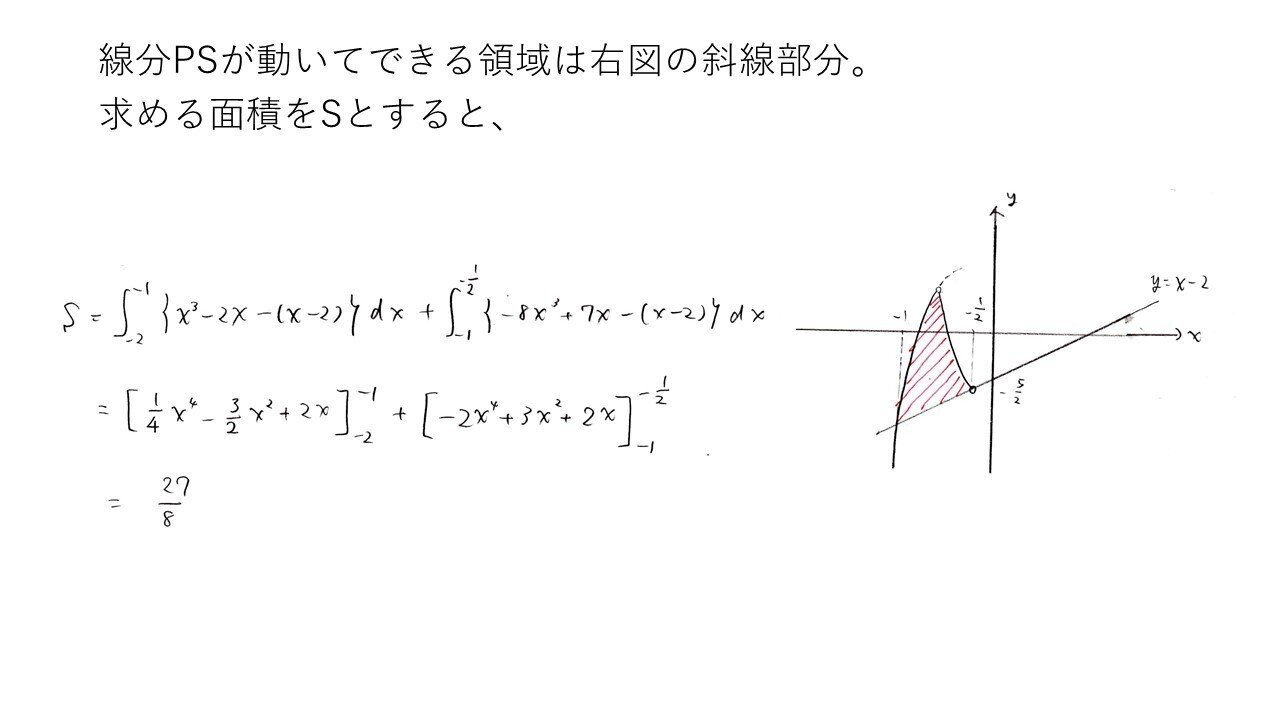
<分析>
おまけ。(2)ができれば、共テレベルの数Ⅱ積分計算です。
<感想>
駿台全国模試で出てきそうなレベルですね。
(1)にしてはやや重い問題でした💦(2)はxの範囲を求めるのに手こずったかもしれません。
(3)がオマケ問題なだけに何とか(2)を確保したいところですね~😅
第5問

【解答】
(1) 標準

<分析>
argとはargumentの略で「偏角」を表します☝
3点が異なる場合については、解答のようにargを用いた議論ができるでしょう💡では、少なくとも2点が一致する場合はどうなんだ?・・・て話ですが
この場合も1点か直線になるため「3点が同一直線上」という条件は自動的に満たします!
(2) 標準~やや難

<分析>
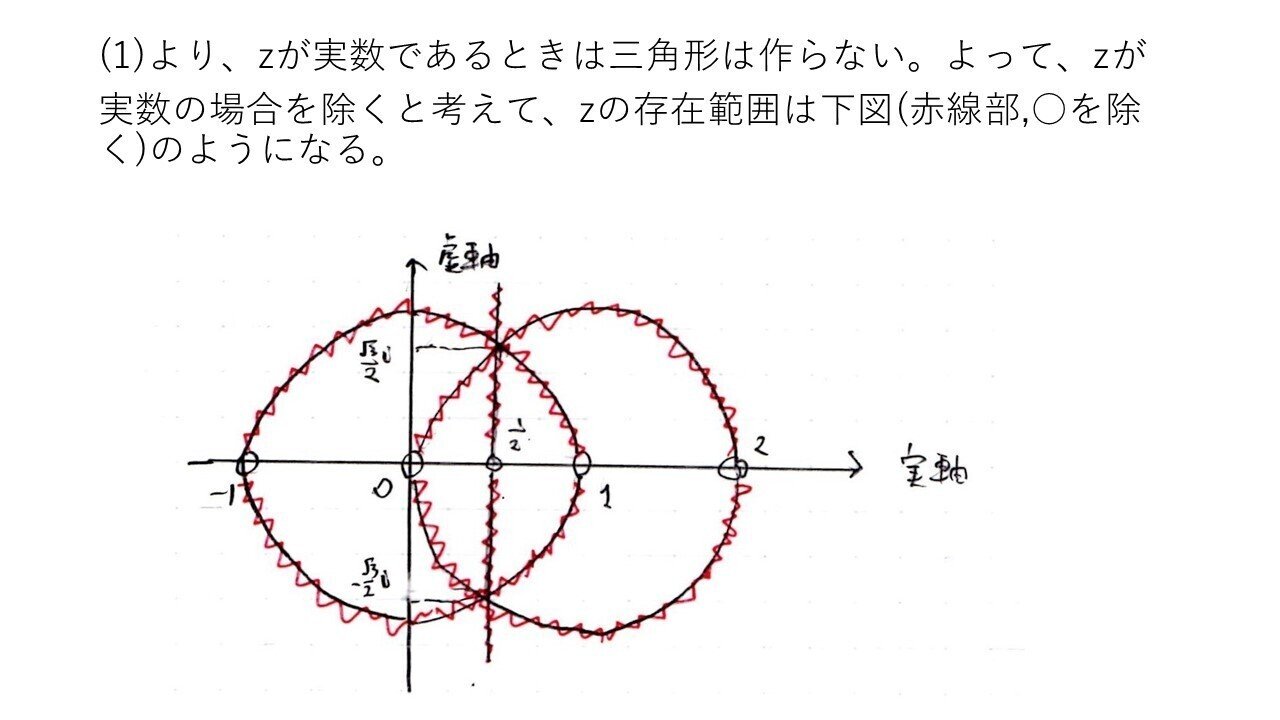
複素数の学習が不十分な人は、|z| =|z-1|が何を表すのか不明だったかもしれません😵
でも、意味を考えればわかります。
「|z-0| =|z-1|は点0からの距離と点1からの距離が等しい点の集合」を表すことから、点0,1の垂直二等分線(z=1/2)とわかります。
(3) やや難

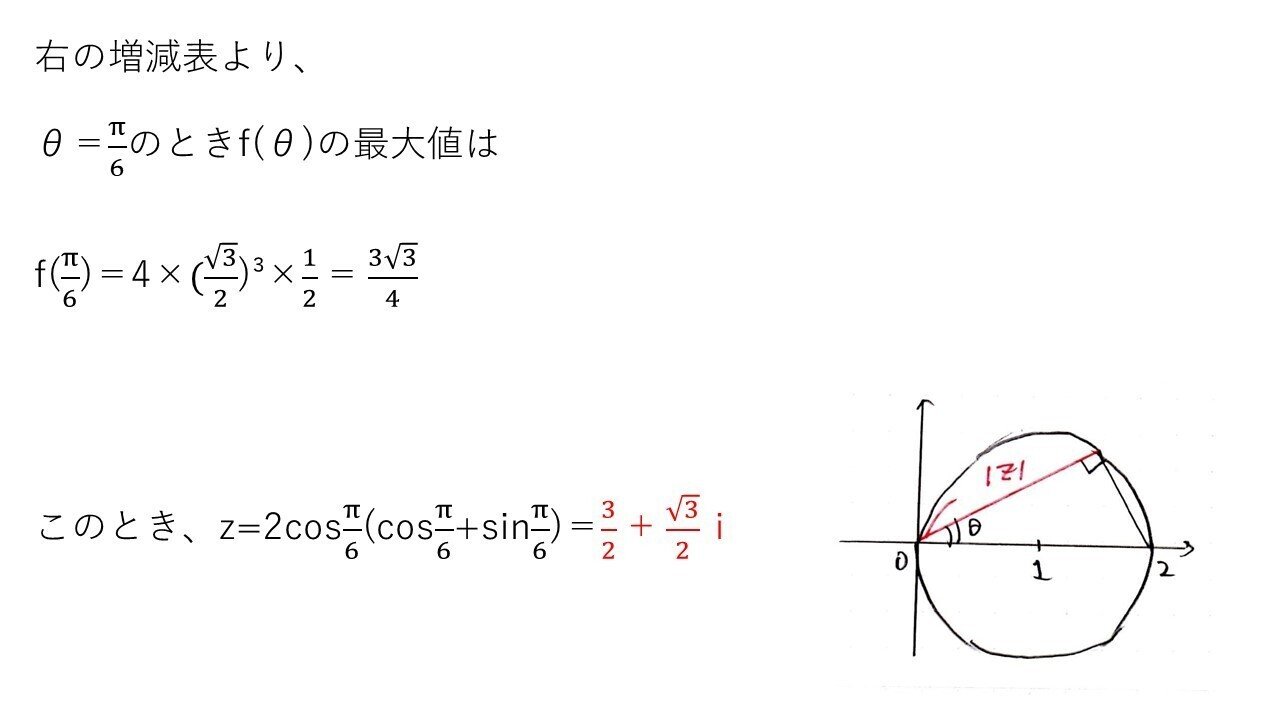
<分析>
(3)は (2)の図示が正しくできれば、数Ⅲの微分の問題となるので、(2)ができればできます。
ただし、「同じ角θで|z|が最大になるときの|z|はどこか?」を特定する必要があり、そこが少し難しいかな?と思いました💦
第6問

【解答】
(1) やや難
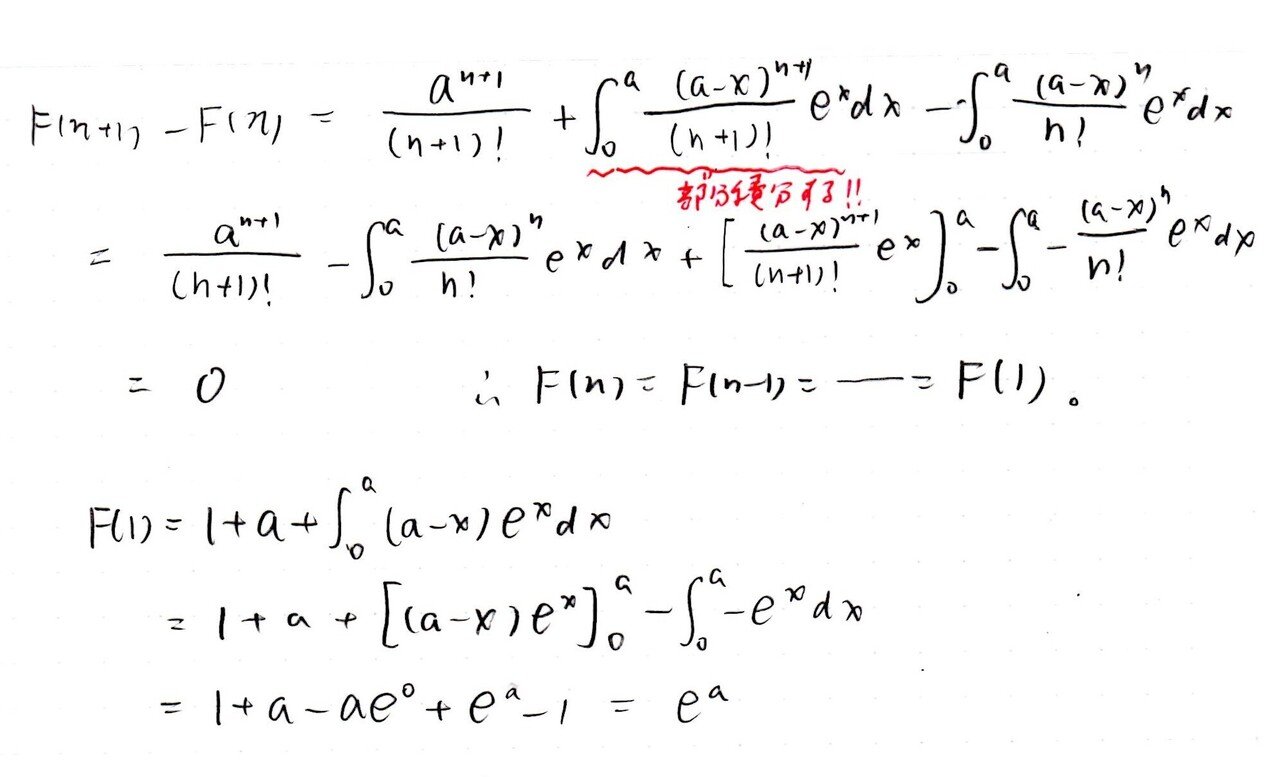
<分析>
(1)にしては重厚で難易度が高めです。
ただ、(2),(3)は(1)と無関係に解けるし、難易度も(1)より低いので、諦めずに取りましょう🧐
①
左辺e^aが定数であることに着目すると、右辺の変数nの式(F(n)とおく)も定数であることを示せばOKです💪そのためには、長い和の部分を消すためにF(n+1)-F(n)=0を示せばよいでしょう!
②
(a-x)ⁿ⁺¹ e^x 部分については、部分積分により(a-x)ⁿe^xの形が出て消えそうだな・・・と考え、部分積分を実行しました。
③
F(n)=F(n-1)=・・・=F(1)がいえるため、最後にF(1)を求めて、F(1)=e^aであることを示します。
(2) 標準
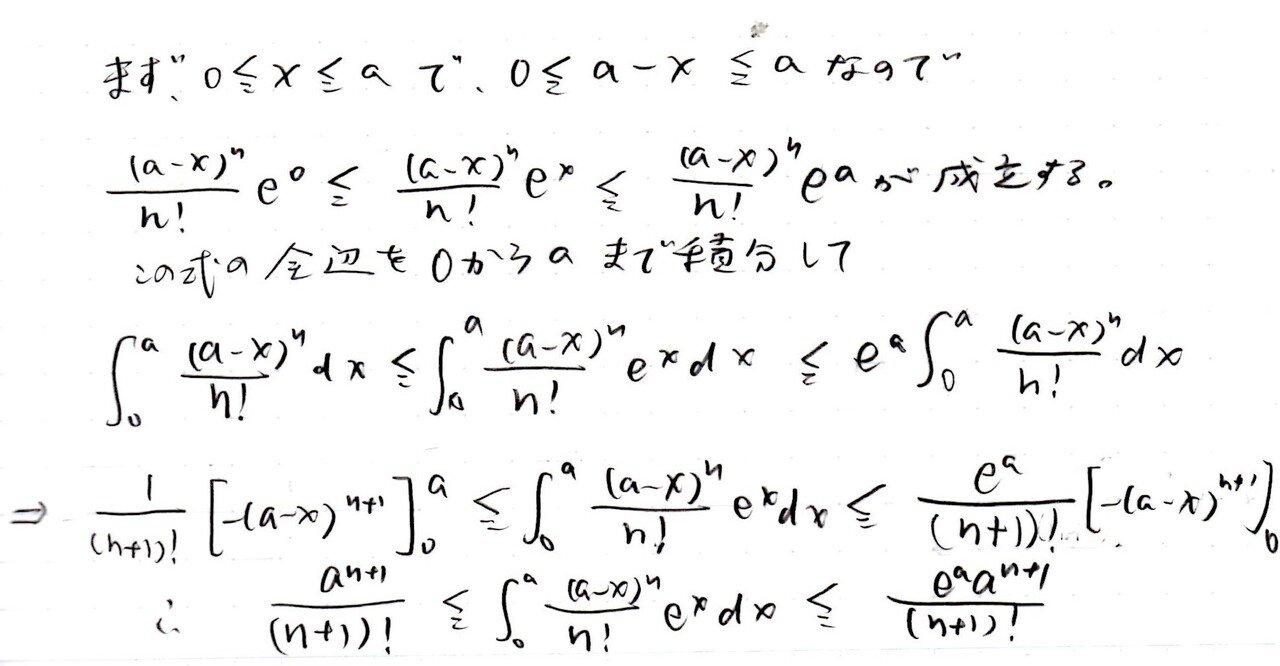
<分析>
不等式の左辺にaⁿ⁺¹、右辺にe^aが存在することより、真ん中の∫(積分)内の式に何らかの操作を施す必要があるな~と考えます🧐
0≦x≦a⇒1≦e^x≦e^aに着目すると、∫(積分)内を(a-x)ⁿのみの形にできます。
(3) やや易
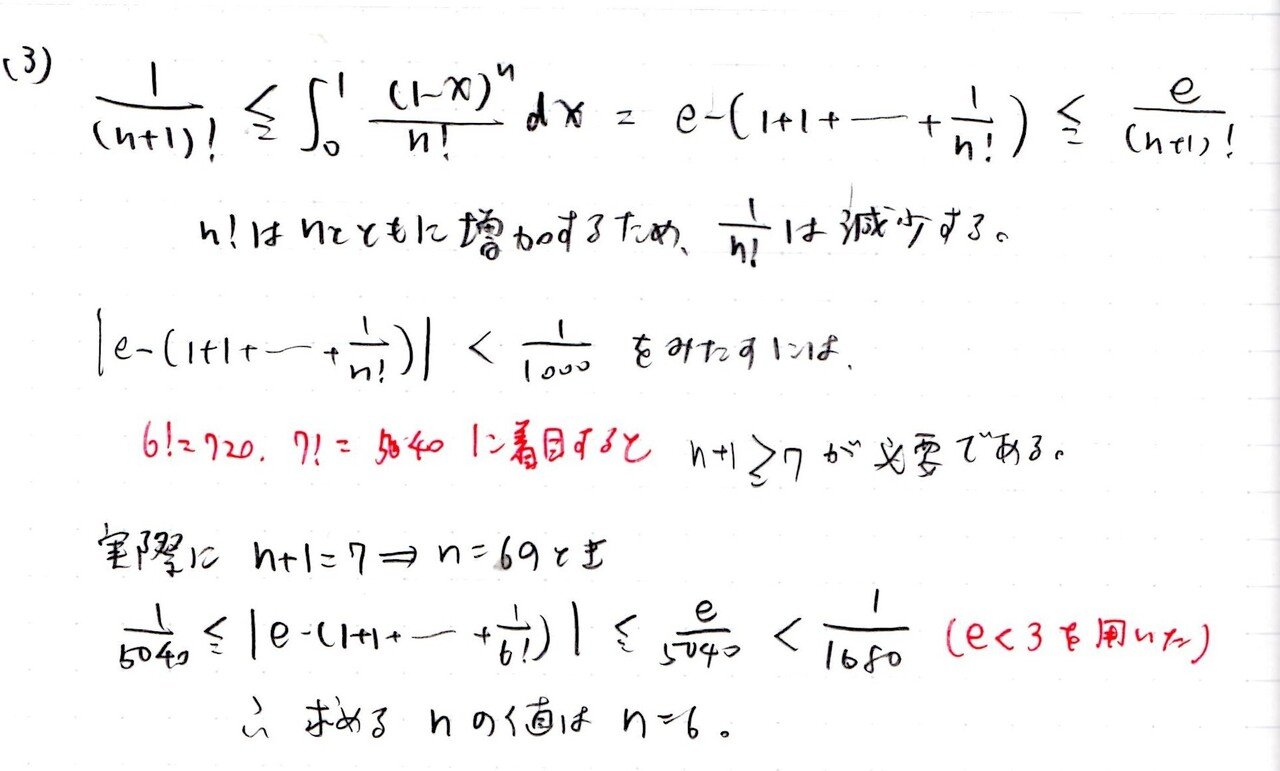
<分析>
(1)の結果と比較すると、a=1を代入したいのはミエミエでしょう👀
a=1を代入して(2)の不等式を利用すると、結局はe/(n+1)!が1/1000より小さいことを言えればよいということがわかるでしょう💡
総括
完答しやすい大問は第1,2問くらいで、第3~6問は半分以上なら取れるか?という感じのい難易度でした。まあ簡単ではないです💦
第1,2問をクリアし、第3~6問でいかに得点するかが合否を分けたと思います。
合格点は
非医:50~55%
医:70~75%
というところでしょうか。
医志望なら
第5,6問の(1)から躓くのは避けたい
ですね。
最後に、再度公式ラインの紹介をします。
私の公式LINEでは、無料相談を随時受け付けております。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってみてください✊
【⬇️公式LINE登録はこちら⬇️】




