
受験生の皆さん、こんにちは。
東大合格ビジネスマンのワタシですm(_ _)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ 3大基礎力重視の裏ワザ勉強法
について、様々な情報を発信しております📢
2022年大学入試、旧帝大の第4弾は「東京大学」です。
当ブログの解説記事は、読者の成績を最難関レベルまでグングン伸ばすことを目標にしており
読者が必死に3年間努力すれば東大(理三以外)・京大(医以外)・九大医レベルに80%以上の確率で合格できることを目的に作成しています✊
市販の問題集のように、解法を丁寧に示すだけではありません!多角的なアプローチで問題を解きほぐしています✊
① 各問の難易度
② 他分野や一般常識との関連事項
③ 問題の躓きポイント
④ 極力曖昧な表現をしない説明
を示しています。
イマイチ成績が突き抜けられない受験生に貴重な情報が提供できればと思いますm(__)m
私の公式LINEでは、無料相談を随時受け付けております。
公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってください✊
私も苦手科目は先生に頼りました。
また、LINE登録していただいた方には
無料プレゼント(1年で偏差値70出す画期的勉強法)
を贈呈します🎁
【⬇️公式LINE登録はこちら⬇️】

東大理系数学の特徴
東大の理系数学は150分で全6問です。数学の実力があれば理科や英語よりは時間的に楽ですが
ほとんどの受験生は結構悩むので時間は足りないのが通常です。
一般受験生の感覚では、標準~やや難×2、難×2、激難×2みたいな出題内容です。
これが東大理系のボーダーからすると、やや易、標準、やや難~難くらいになるのでしょうが🤔
理一で60点、理二で50点、理三で80点程度あれば、数学で足を引っ張るということはないでしょう。
別の言い方をすれば、それくらいムズイってことです💔
さて、今年の理系数学の難易度はどんなもんだったのでしょうか??
第1問

【解答】
(1) 易〜やや易
<分析>
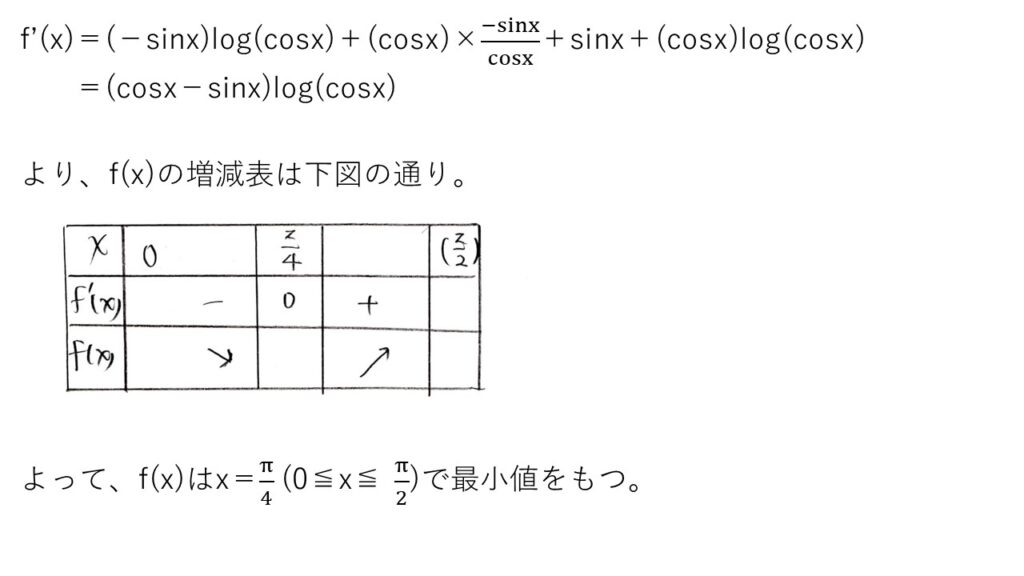
最小値があることを示したいので、定石通りに微分でしょう☝️それに、微分することで∫も消えますし。
f'(x)が出たら正負の判定です。範囲が0≦x≦π/2なので、cosxは単調減少,sinxは単調増加です。これに着目すると、f(x)の増減も判明します。
(2) 標準

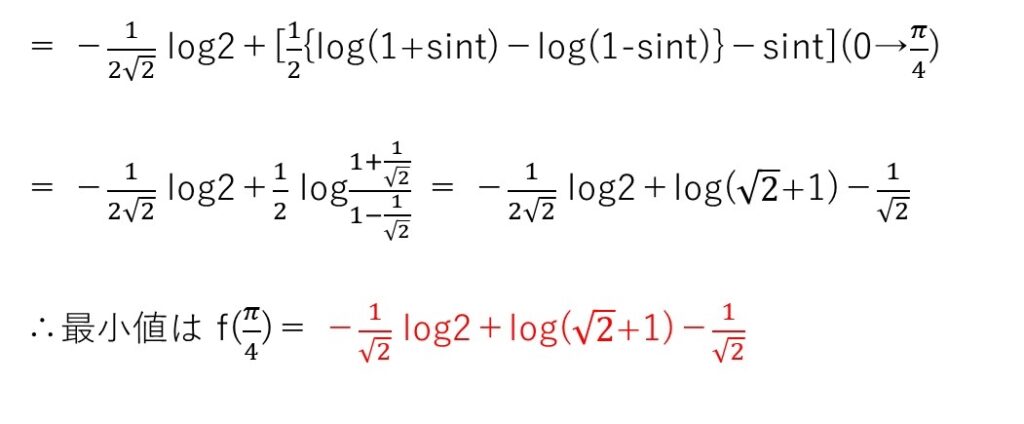
<分析>
∫(cost)log(cost)dtですが、これは∫xlogxdxと同様に部分積分を使いましょう。あとは、計算が少し面倒ですが、よく見るタイプの計算です。
マトモな東大受験生なら∫dθ/cosθの計算は大丈夫だと思います💦
三角関数が絡む積分ではsinθとcosθを共存させるとうまく処理できることが多いので、∫dθ/cosθの変形もそれを狙った変形と解釈できます☝️
<感想>
難化が囁かれた2022年東大理系数学ですが、第1問は全然よくある標準問題でした。後にヤバイのが控えているのか?
理三受験生なら第1問は完答しておきたいですね🤔💔
第2問

【解答】
(1) やや易

<分析>
a₃=5より、a₆,a₉,a₁₂・・・も5の倍数になることを示せばいいのかな?と思うはず。ここは、数学的帰納法を思いついてほしいですね💡
実際に、a3mが5の倍数と仮定して、上記の解法でa3m+3も5の倍数であることを示せばOKなのです🙆♂️
(2) やや難

<分析>
発想が難しい問題。漸化式は2乗の存在により解けなさそうだし、ひとまずa₅くらいまで値を出してみましょうか…何か見えてくるかも🤔❓❓
a₁=1,a₂=2,a₃=5,a₄=26,a₅=677であり、(1)よりa₃,a₆,a₉…が5の倍数であることが示せました。
ここで、漸化式の1をa1で置き換えてみましょう💡すると、an+2=(anの倍数)+a2、an+3=(anの倍数)+a3より、なんかn+n=2nがanの倍数になる気がしませんか?
それを3n,4n・・についても考えると、どうもn=mk(mは自然数)が答として浮かんできますよね🤔
(3) やや難〜難

<分析>
(2)が解けないと無理なのが痛いところ😥
2022=2x3x337、8091=9x29x31より2022と8091の最大公約数は3。(2)の結果を利用すると、a₂₀₂₂はa₉,a₂₉,a₃₁の倍数にはならず、a₈₀₉₁もa₂,a₃,a₃₃₇の倍数にならないですね。
よって、a₂₀₂₂とa₈₀₉₁の最大公約数はa₃、つまり5となるのです☝️
<感想>
(1)は取りましょう。間隔3なので、帰納法でゴリ押せば示せますよ✊
正直、(2)の出来不出来で差が付きました。(3)を直接示すのは無理なので、(2)の結果をうまく利用します。
理一、理二は(1)が取れればOKなんですが、理三は(2)を取れないとややビハインドかも?
第3問

【解答】
(1) 易〜やや易
<分析>
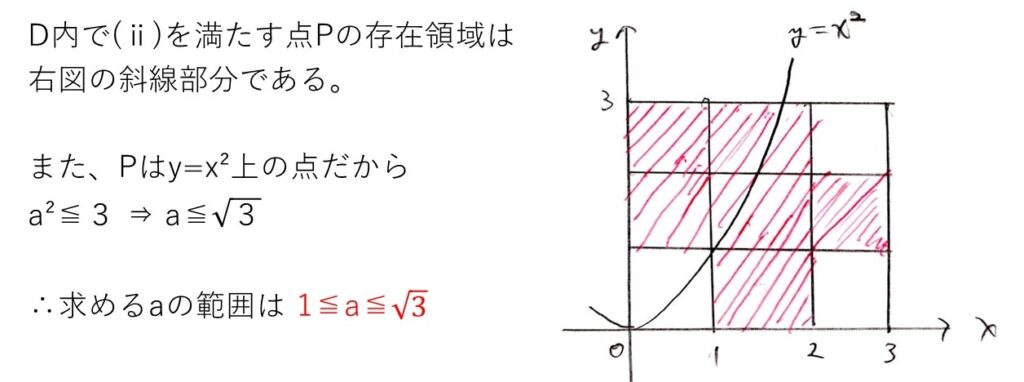
面倒くさがらずにちゃんと条件を把握しましょう☝️
聞いていることは実は簡単で、領域D内においてO,A,Bから十分離れていない領域を除き、かつy=x2上にあるような点Pの位置を把握すればOKなのです🙆♂️
(2) 標準〜やや難

<分析>
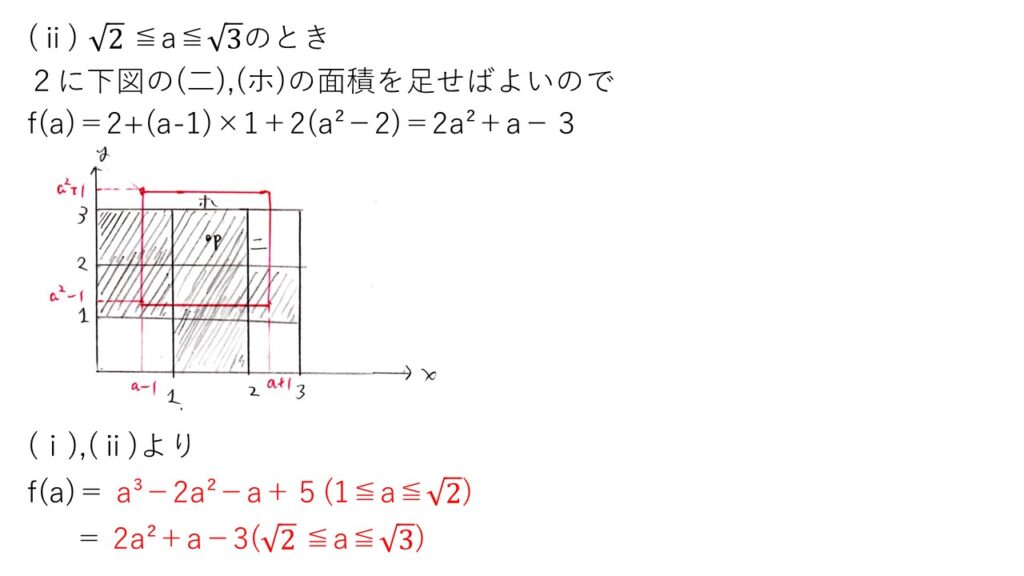
点P(a,a²)回りに1辺の長さ2の正方形を考え、(1)で除いた部分からさらに4を引き、オーバーラップした部分を加えることでf(a)を求めます。
(3) やや難

<分析>
(2)ができれば微分するだけの問題なので、難しくはないでしょう。
<感想>
第2問よりは完答難易度は低いでしょう。(2)も「十分離れている」の意味を図形的に把握できれば何てことありません。
本問は、第1問に次いで完答が望ましい問題でした☝️
第4問

【解答】
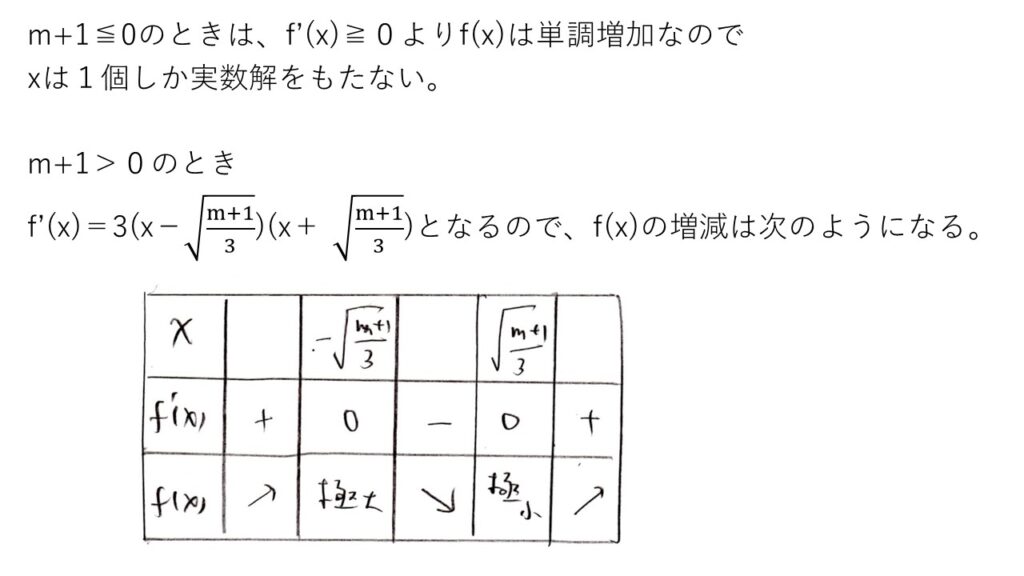
(1) 標準~やや難


<分析>
とりあえず、点Pを(a,b)とおいてPを通る傾きmの直線を用意しようと考えるのは、演習経験のあるマトモな東大志望なら思いつく内容です。
また、3点で交わる条件を「f(x)=0を満たすxが3個存在する」と解釈するのも難しくないでしょう。
あとは、極小値と極大値の積が負であることより②の式を出すのですが、②は3次の係数が負のmの3次関数なので、いずれ負になることは自明でしょう🚩
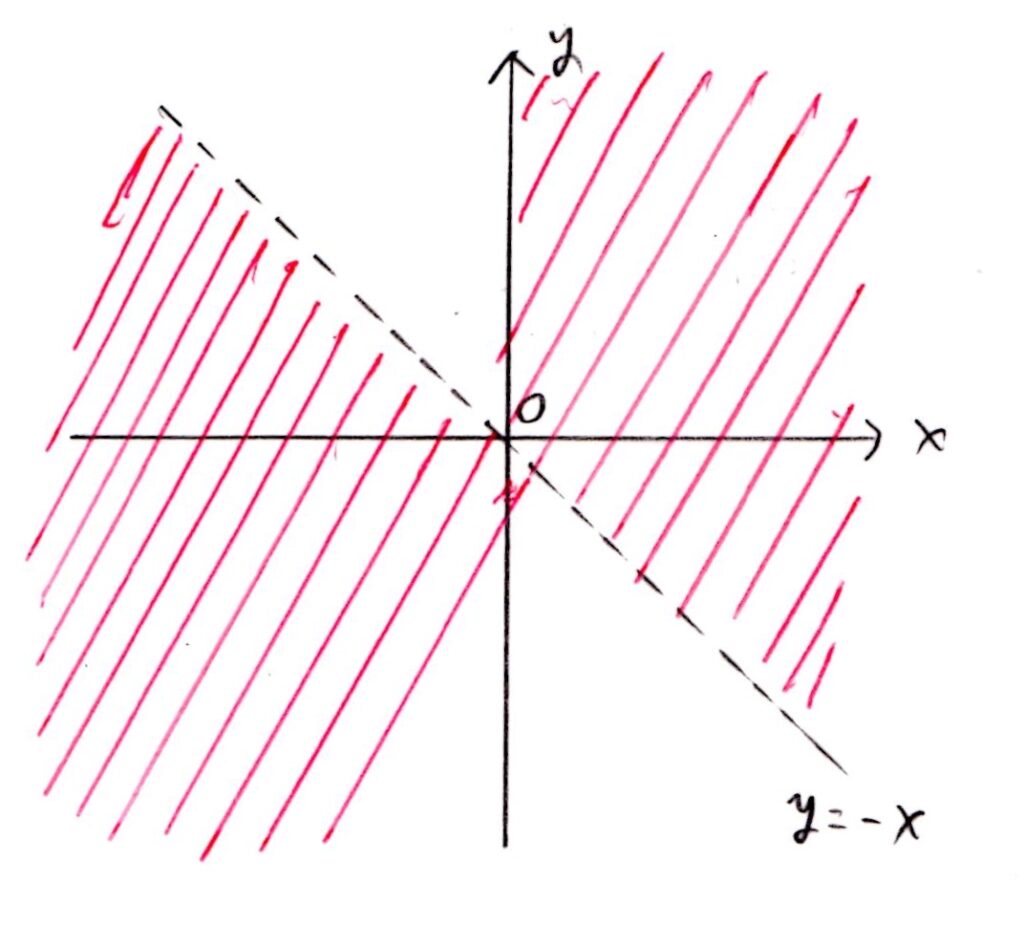
(2) やや難



<分析>
積分を用いた面積計算をすることは明らかですから、3つの解α,β,γを定める必要があると考えられます🤔
α,γの条件式は結果的にかなりシンプルな形になるのですが、それを出すまでの計算で気力が削られそうです💔
最後は、「直線y=(α²-1)xの通過範囲=点Pの存在範囲」と発想の転換をしましたが、それは「点Pがy=(α²−1)x上にあって、原点を通るように直線を引くと、条件(ⅱ)を満たすようになる」と考えたからです。
<感想>
発想面では言うほど難しくはないのですが、計算処理が結構重いですね💦
(1)はなるべく取りたいとして、(2)もα,β,γを設定してα+γ=0を導くところまではこぎ着けて部分点を狙いたいところですね🤔
第5問

標準〜やや難
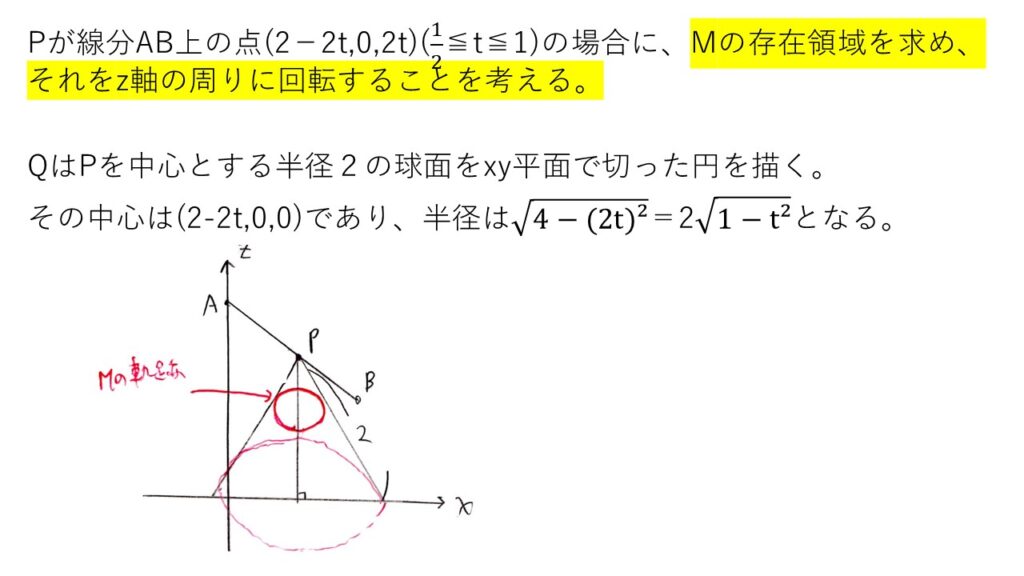
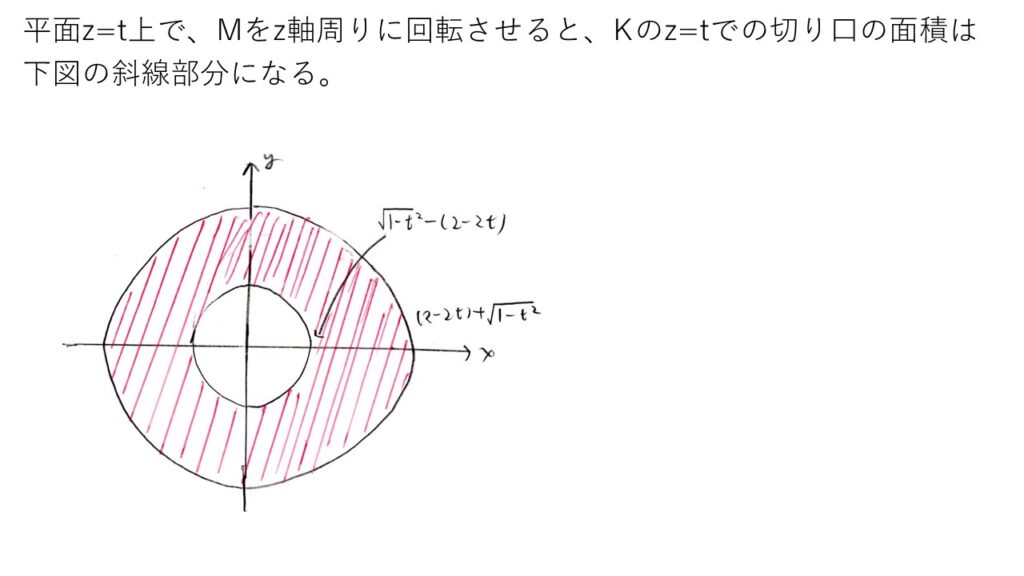
【解答】

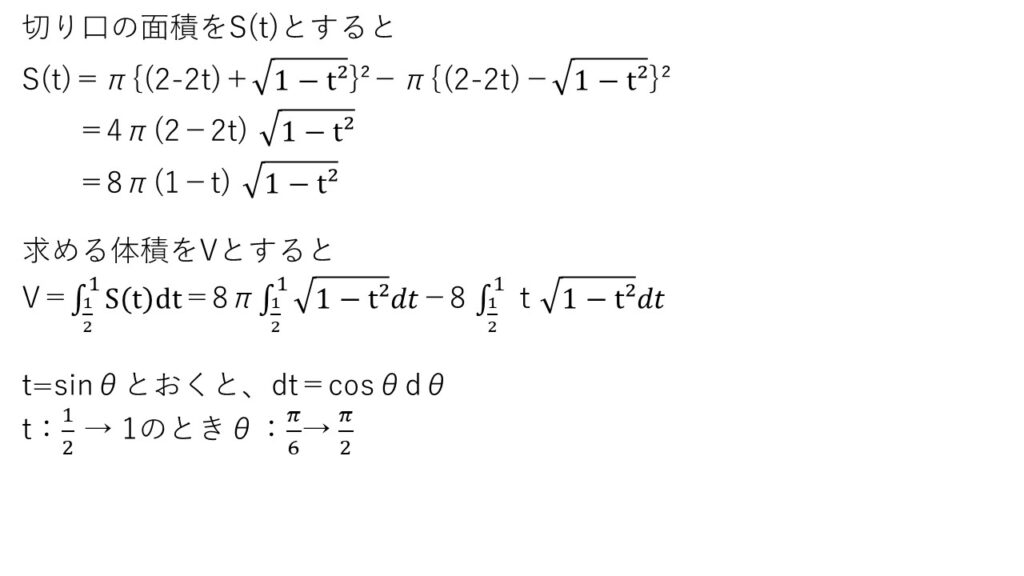
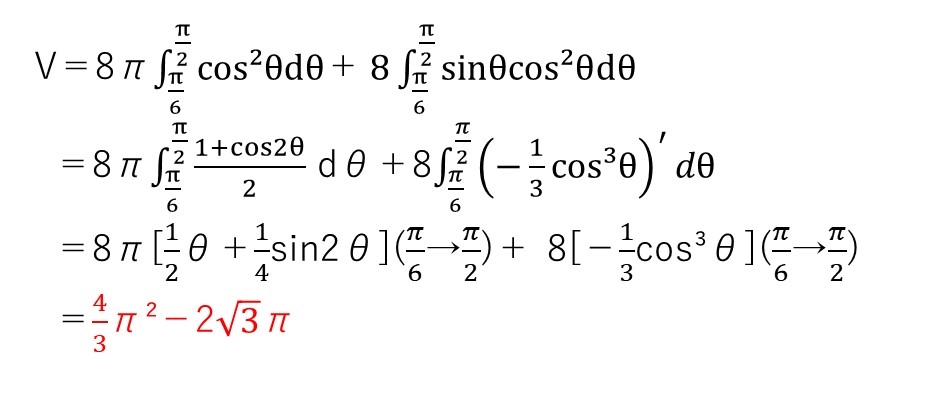
【感想】
なんか2020年第5問,2017年第6問を組み合わせたような問題ですね🤔
平面の方程式を使うのか?と身構えていたのですが、結局使わなかったですね💦
点Pを回してから考えるのではなく、まずPを直線上に定め(1次元)、Q,Mの軌跡(円)を出し(2次元)、その円をz軸まわりに回すという解法をとっています。
2017年第6問もそうでした…あれは平面の方程式使ってましたけど🤔
第6問

【解答】
(1) やや難
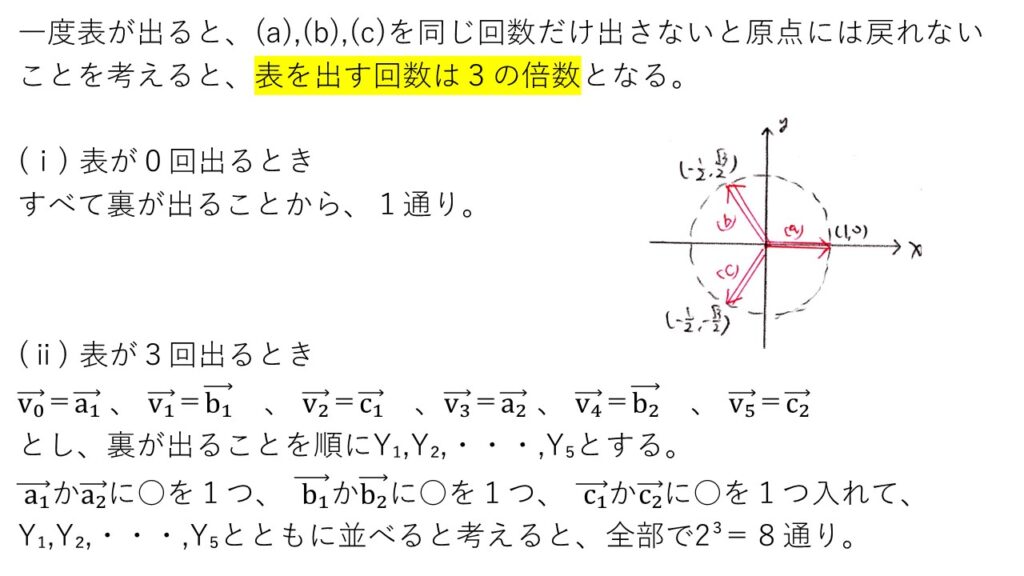

<別解>
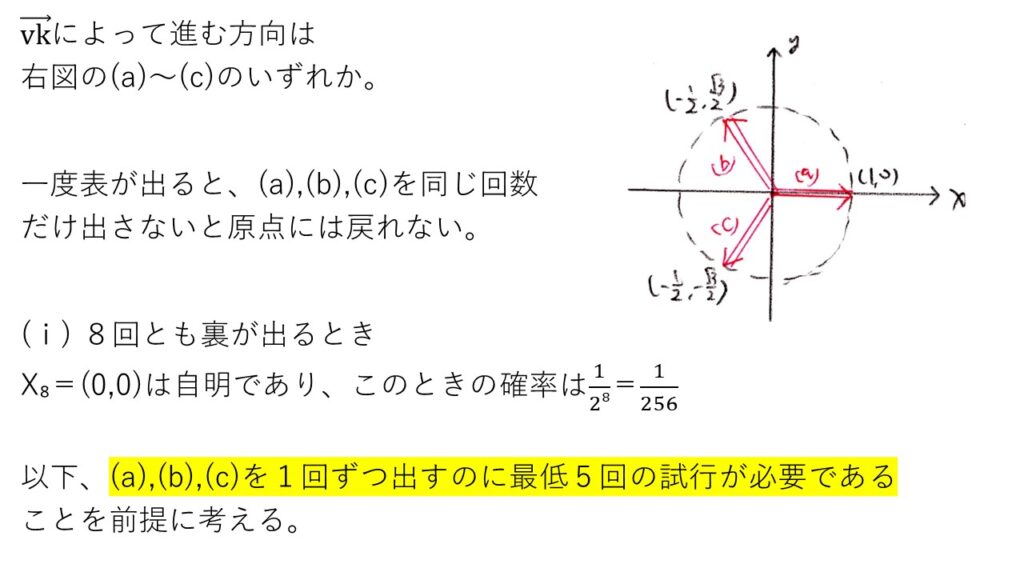



<分析>
裏が出るたびにvkの値は変わりますが、実験していくと、一度でも表が出ると結局は3方向すべて出さないと原点には戻れないことが判明します🚩
よって、表が出る回数は3の倍数です。
(別解)のように虱潰し的に数え上げることもできるのですが、非常に見落としやすく、正解するのは至難の業だと思いました😭
(2) 難


<分析>
(1)で重複組合せの考えで解けなかった受験生は(2)で沈没したものと思われます。
私も(1)を数え上げでゴリ押したため、解けませんでした💔
最終問題だし、時間ないしで・・・理Ⅲでもできなくて全然支障ないと思いますが💦
<感想>
(1)で規則性を発見するのはさほど難しくないですが、重複組み合わせの考え方に疎いと、一気に難問化したのではないか?と思います。
私が場合の数苦手・・・というのもあるのですが、第6問が第2問と匹敵して今年の最難問ですかね~💦💦
総括
全体的に見て、第1問,第2問(1),第3問(1),第4問(1)は標準的で全然取れるので、ちゃんと基礎を理解している受験生なら40~50/120点は鉄板で取れたはず✊
差が付くのは第2問(2)(3)、第5問でしょうか。理Ⅲ受験生はこれらをいかに得点できたかで合否が分かれたでしょう🥲
第6問は重複組合せの考えに免疫があったかどうかで差が出たでしょう。
120点満点中、合格点は
理Ⅰ:50~55点
理Ⅱ:45~50点
理Ⅲ:70~75点
程度でしょうか🤔
最後に、再度公式LINEの紹介をします。
公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信する公式LINEはこちら👇
登録していただいた方には、無料プレゼント贈呈🎁の他、無料相談も受け付けております。






