
受験生の皆さん、こんにちは。
東大合格ビジネスマンのワタシですm(__)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ 3大基礎力重視の裏ワザ勉強
2022年大学入試、旧帝大の第2弾は「東北大学」です。通称「とんぺー」😂
当ブログの解説記事は、読者の成績を最難関レベルまでグングン伸ばすことを目標にしており、
読者が必死に3年間努力すれば東大(理三以外)・京大(医以外)・九大医レベルに80%以上の確率で合格できることを目的に作成しています✊
市販の問題集のように、解法を丁寧に示すだけではありません!多角的なアプローチで問題を解きほぐしています。
① 各問の難易度
② 他分野や一般常識との関連事項
③ 問題の躓きポイント
④ 極力曖昧な表現をしない説明
を示しています。
イマイチ成績が突き抜けられない受験生に、貴重な情報が提供できればと思いますm(__)m
私の公式LINEでは、無料相談を随時受け付けております。
公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってください✊
私も苦手科目は先生に頼りました。
また、LINE登録していただいた方には
無料プレゼント(1年で偏差値70出す画期的勉強法)
を贈呈します🎁
【⬇️公式LINE登録はこちら⬇️】

東北大理系数学の特徴
東北大の理系数学は100分で6問。例年の東北大理系数学のセットは、まあまあ手応えのある標準問題×4、やや難問題×2という印象🤔
さて、今年はどんな問題が出たのか、そして難易度はどうだったのか👀❓
第1問

【解答】
(1) やや易

<分析>
ℓ+m+n=k(ℓ≧0,m≧0,n≧0)を満たす整数(ℓ,m,n)の組数を順列で考える手法は定石として押さえておきましょう☝k個の○と2個のΛを一列に並べる順列に等しくなります。なお、ℓ≧1,m≧1,n≧1のときは(ℓ−1)+(m-1)+(n−1)=k−3とするのがコツです💡
もちろん、nを固定してℓm座標平面で考えるとかもできます。
(2) 標準

<分析>
誤答で75個を答えた受験生が一定数いそうですね🤷♂️同じ奇数が3個ある場合は別個に考える必要がありました💦
(3) やや易~標準
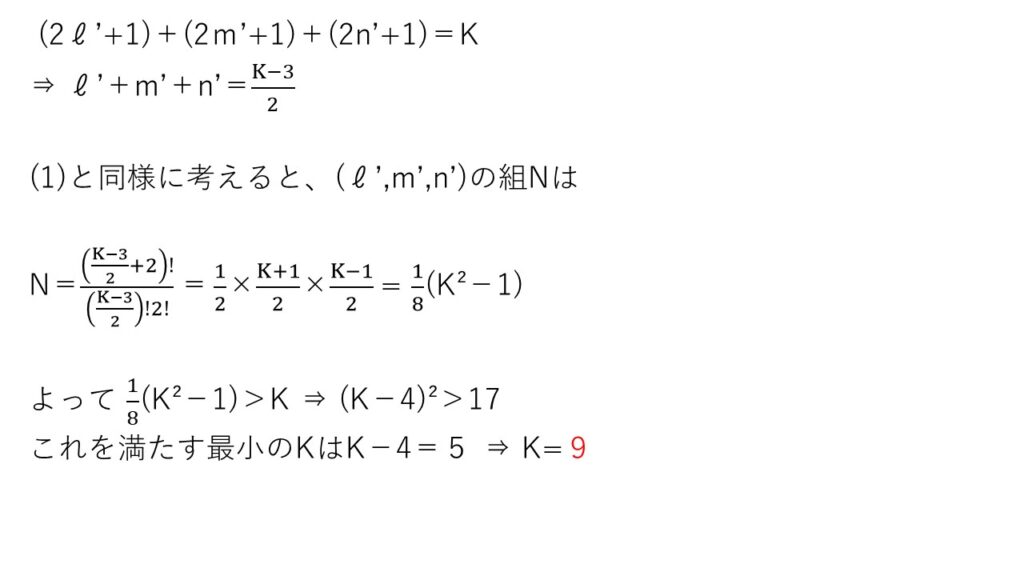
<分析>
(1)の99をKに変えただけで、解法自体は(1)と同じです。あとは、2次不等式を解けば終い。
(2)より簡単ですね・・・しかも、(2)と無関係というのがさらに有難い😂
<感想>
場合の数に関する問題です。(2)で数え漏れでミスる可能性はありますが、本問のキモは(1)のℓ’+m’+n’=48を満たす(ℓ’,m’,n’)の組数を求められたかでしょう。別に座標平面で考えても解けますが、同じ物を含む順列の解法は是非習得しておきましょう✊
第2問

【解答】
(1) 易~やや易

<分析>
(x+1)²がx=−1で0、x≠−1で正になることに着目すると、結局はx²+3x+aが負になるようなxが存在すればよいとわかりますね☝また、y=x²+3x+aの軸がx=−3/2なので、x=−3/2のときに負の値をとればOKなのです💪
(2) やや難〜難
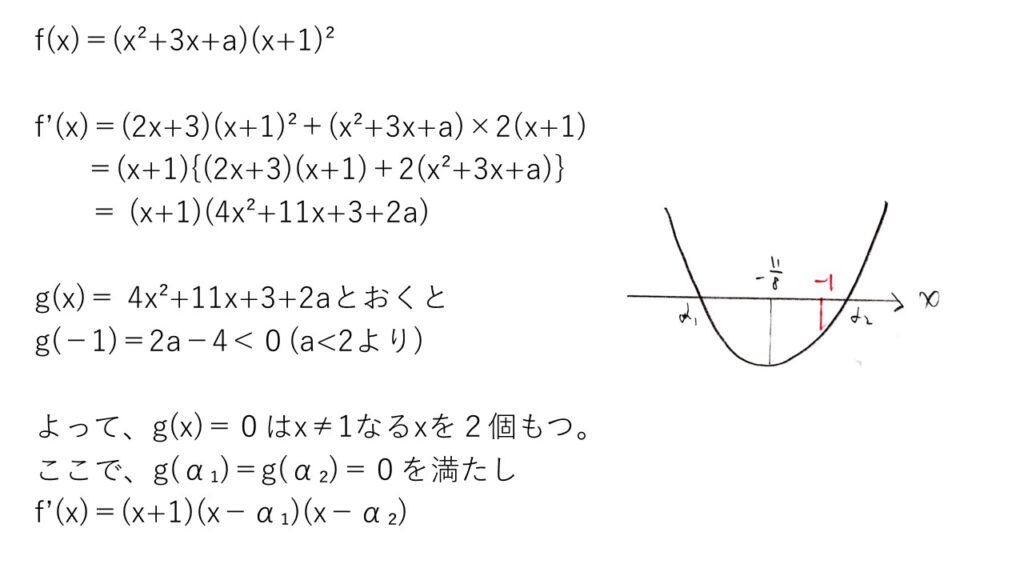
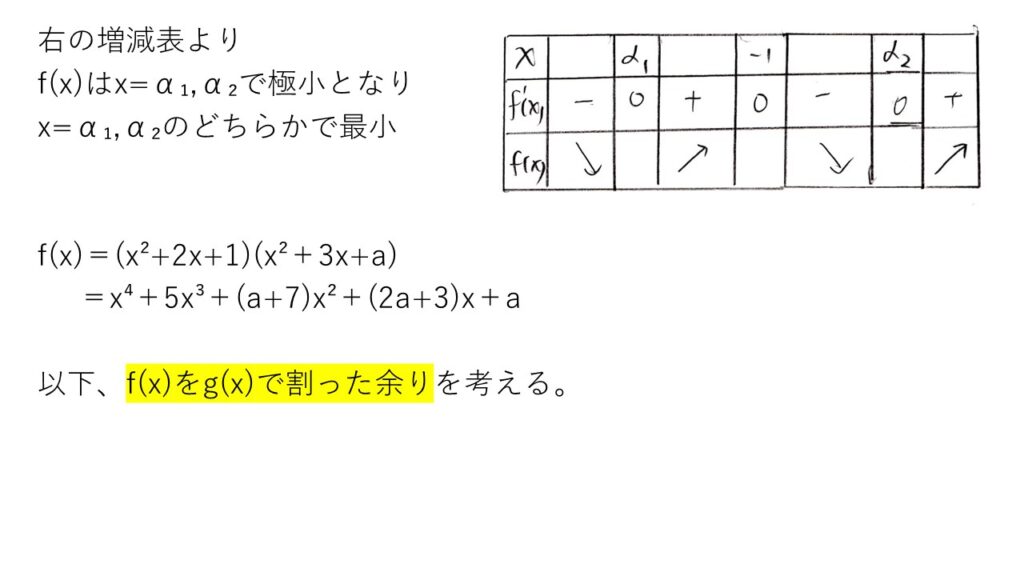

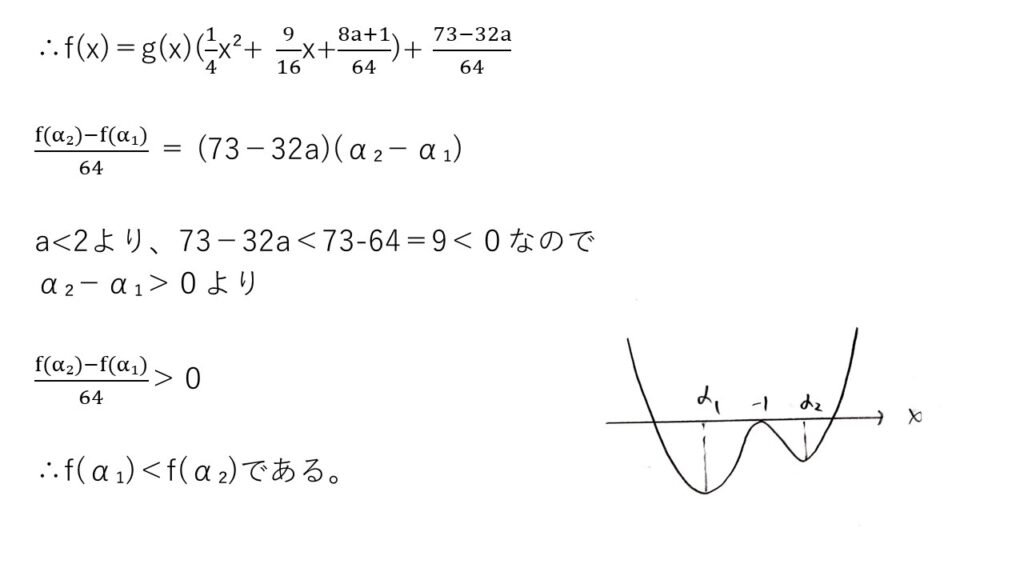
<分析>
f'(x)=(x+1)(4×2+11x+3+2a)を出し、g(x)=4×2+11x+3+2aとおいたときにg(-1)<0を出すまでは問題ないでしょう。問題はその後のf(α1)とf(α2)の大小チェックですが…これがまたムズイ👺
4乗,3乗の引き算をマトモにするとカオスでしょうから、ここは、g(α1)=g(α2)=0に着目してf(x)をg(x)で割り算して次数下げを試みます☝️それでも計算がカオスだけど🥲
(3) やや難〜難

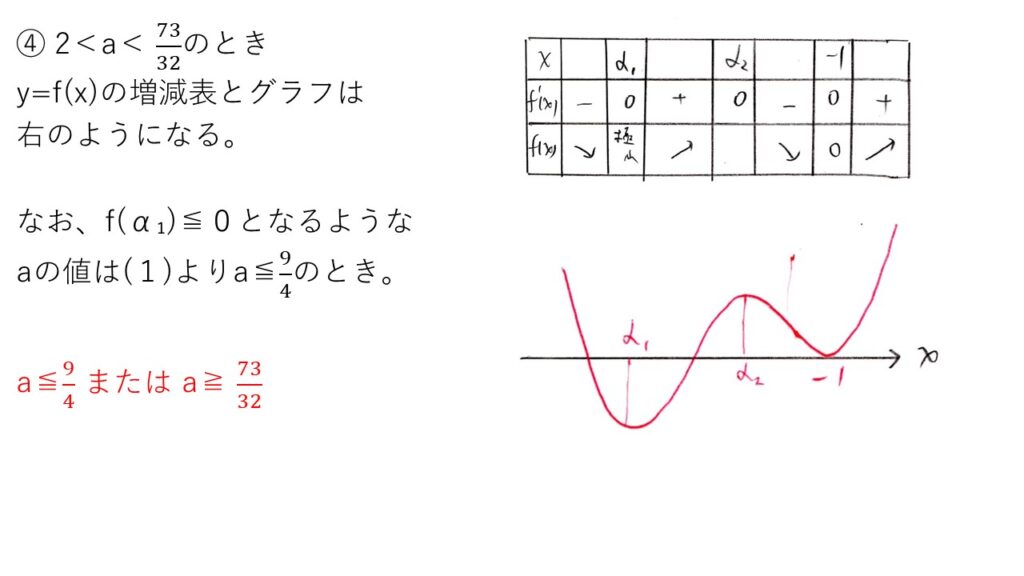
<分析>
(2)ができれば見えるんじゃないでしょうか👀
<感想>
これはマジムズイ…今年のセット最難問でしょう😀💦
特に、(2)の極小値を2つとると言った後の処理が鬼畜ですね👺東北大であることを考えると、医学部志望者でも(1)◯で(2)は部分点で問題ないでしょう🤥💦
第3問

【解答】
(1) やや易
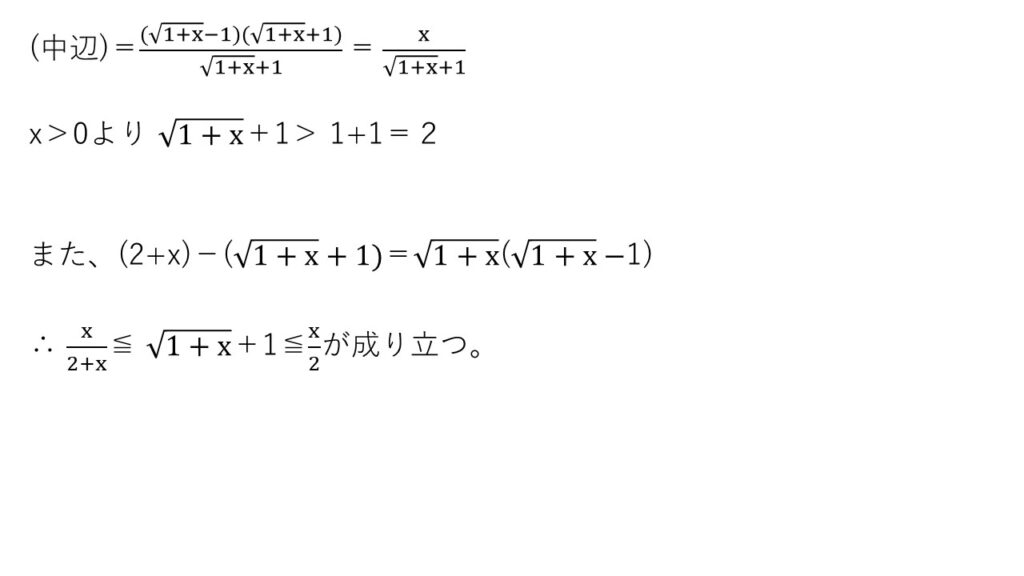
<分析>
中辺の形を見て有理化を思いつけば、非常にシンプルに解答できます☝
もちろん、辺々を引き算して微分でも求められますよ🚩
(2) 標準~やや難
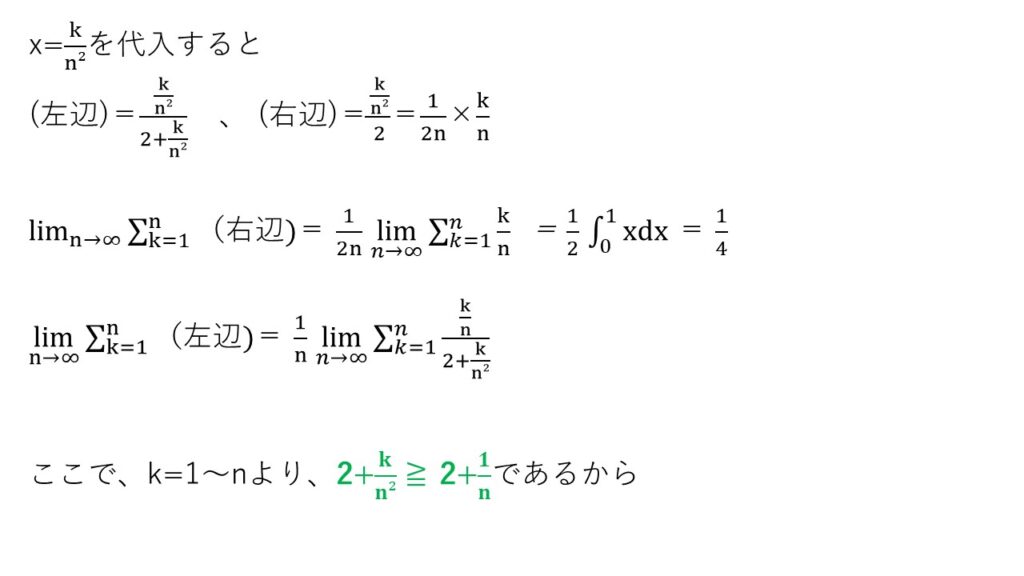
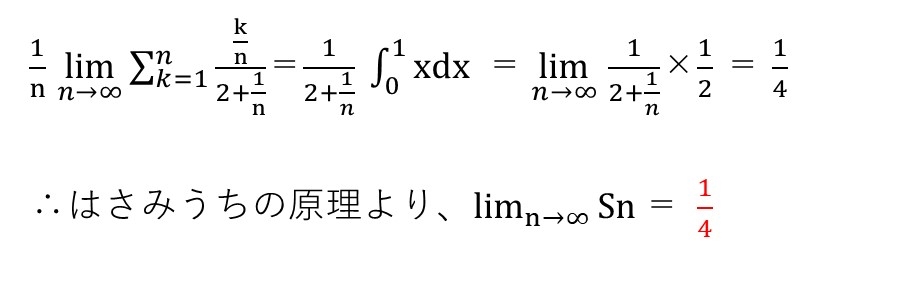
<分析>
右辺の証明は簡単!まんま区分求積法です。問題は左辺ですが、分母・分子とみにk/nが含まれていて非常に扱い辛いですね~🤷♂️ここで、分母の最大値が2+1/nであることに着目して、はさみうちを意識した証明に持ち込みます✊
<感想>
(1)は有理化が思いつかなくても、辺々引いて単調減少(増加)の常套パターンに持ち込めば解けます。
(2)も右辺は見るからに区分求積法で楽勝ですが、勝負は左辺の上手な変形でしたね💦分母,分子ともk/nの形ならまだ簡単だったと思いますが、k/nとk/n²なんで・・・一方を消す発想を得たいところでした🤔
第4問

【解答】
(1) やや易
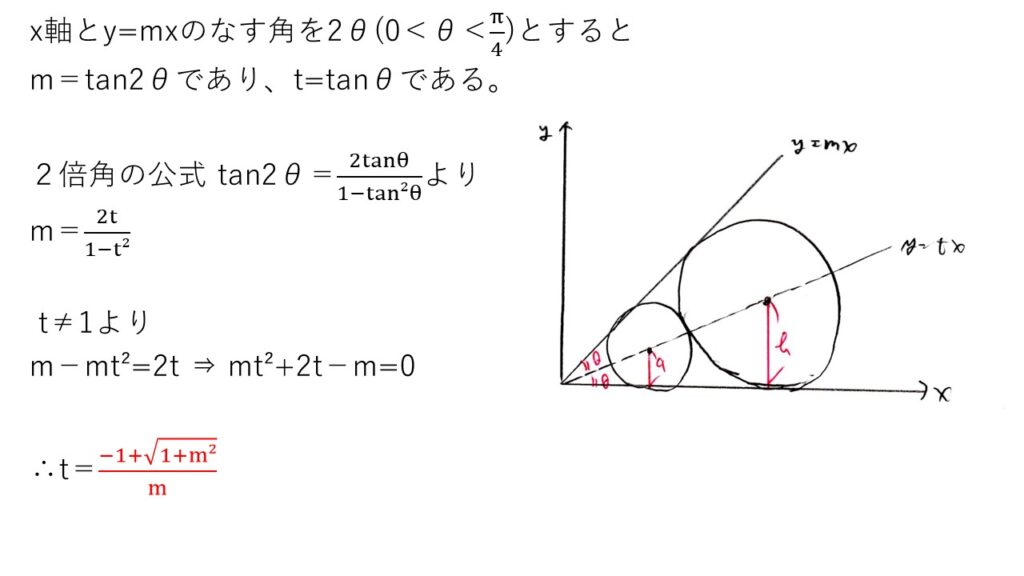
<分析>
円外の点から円の中心を通る直線を引くときにx軸とy=mxのなす角を二等分するのはOKでしょうか??覚えていなくても、三角形の合同から簡単に出るんですが🤔💦
(2) やや易

<分析>
上記の幾何的な解法はどこかで見覚えがあるのでは👀❓直角三角形の斜辺が2円の半径の和になることがポイントですかね~🎵
(3) 標準

<分析>
何のために(1),(2)でmとb/aをtを使って求めたのか?を考えると、(3)をtだけの式で表せばいいのかな?という推測が立つと思います。実際、tのみの式で表すと、うまいこと分母のtが消えました💡
<感想>
(1),(2)とも平面座標というよりは平面幾何的な問題でした。大学受験でも中学で学習する平面幾何は多用するので、超苦手な方は中学数学に戻って、幾何を復習してみるとよいでしょう☝
(3)は極限の問題ですが(1),(2)でmとb/aをtで求めさせる誘導があることからtのみで表現する発想をしたいところでした。「誘導は何のためにあるのか?」を常に意識しましょう💡
第5問

【解答】
(1) やや易


<分析>
ℓはaに平行でℓ’はbに平行であることにまず着目します👀
さらに、垂直条件からの内積=0を利用して、sn,tnを含む式、tn,sn+1を含む式を導出します。最後に、tnを消去すれば、sn+1とsnの関係式が出ます。
(2) やや易
<分析>
(1)の漸化式を解くとsnの極限値は楽勝で出ます。tnの極限値については、(1)の過程で出たsnとtnの関係式を用いればOK!
(3) やや易

<分析>
これは(2)までできた受験生にとっては完全におまけでした😂😂
<感想>
これは(1)の出来不出来で大きな差がついた問題でしょうね💦💦だって、(2)は漸化式解くだけ、(3)はおまけですから😂
ある意味all or nothingな問題であり、今回のセットでは一番合否を分けた問題ではないでしょうか👀
第6問

難易度:標準~やや難
【解答】
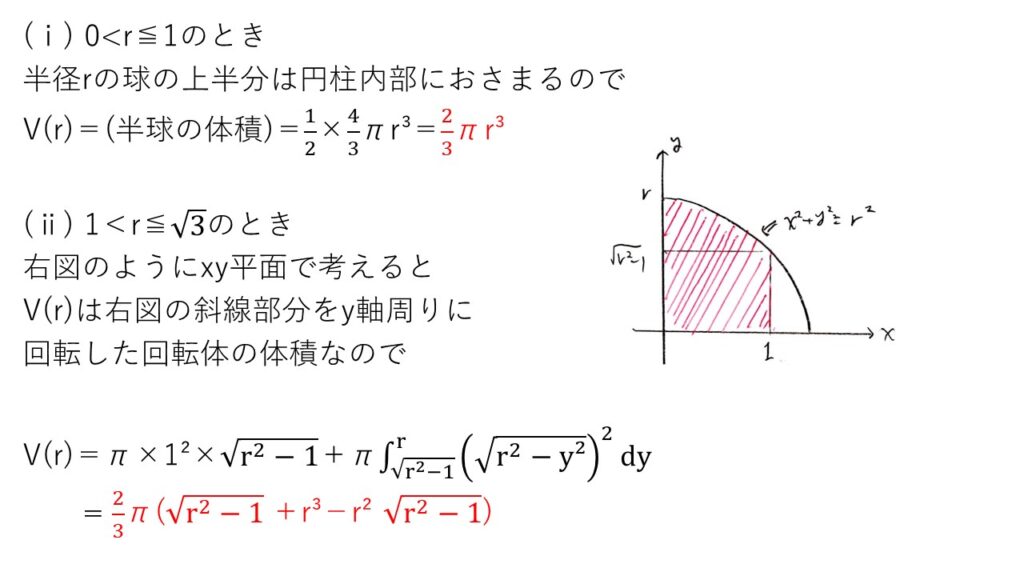
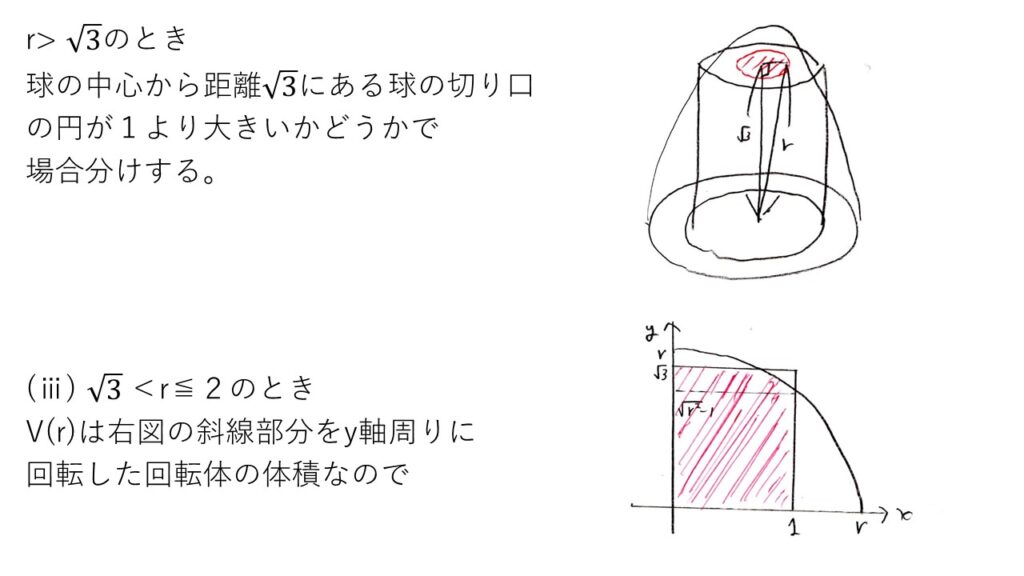

<分析>
円柱の円の半径1、円柱の高さ√3が、まず場合分けの境目になりそうだな?というのは、実際に図を描いてrを大きくしていけば気付くと思います🤔
問題はr=2での場合分けですね!!ここが見落としポイントになりますが、球の中心から距離√3にある半径1の円と比べて球の切り口の円が大きいのか小さいのかで分類するとうまくいきそうですね💡
<感想>
空間図形の問題です。半球も直円柱も円柱の軸に関して対称であることから、軸に垂直な平面で切り口を考えると考えるのは難しくないでしょう。
あとは、rをすごく小さい値からすごく大きい値まで動かしてみて、場合分けの境目を探す姿勢で臨めば、r=1,√3,2が見えるのでは?
r=2はやや盲点ですけどね💦
総括
今年の東北大はやや難化です。第2問を除けば例年並の難易度なんですが、第2問が高得点の取りにくさを助長していました💦
取りやすいのは第1問、第4問、第5問ですが、第5問は(1)の出来不出来で大きく差がつく今年のキー問題と言えそうです💦
あとは、第3問(2)と第6問がやや難しめで、ボーダー層と実力者の差が出る問題だと思います。医学部受験生だと、ここで差がついたかも。
第2問は(1)と(2)の部分点で十分。というか、これ完答できる人は数学満点コースなので、合否には関係ないですね🥲
合格点は
非医:45〜50%
医:65〜70%
程度だと思います🤔
では、以上で解説を終わります🚩
最後に、再度公式LINEの紹介をします。
公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信する公式LINEはこちら👇
登録していただいた方には、無料プレゼント贈呈🎁の他、無料相談も受け付けております。





