
受験生の皆さん、こんにちは。
東大合格ビジネスマンのワタシですm(_ _)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ 3大基礎力重視の裏ワザ勉強法
について、様々な情報を発信しております📢
2022年大学入試、旧帝大の第6弾は
「大阪大学」です。
当ブログの解説記事は、読者の成績を最難関レベルまでグングン伸ばすことを目標にしており
読者が必死に3年間努力すれば
東大(理三以外)・京大(医以外)・九大医
レベルに80%以上の確率で合格できる
ことを目的に作成しています。
市販の問題集のように、解法を丁寧に示すだけではありません!多角的なアプローチで問題を解きほぐしています✊
① 各問の難易度
② 他分野や一般常識との関連事項
③ 問題の躓きポイント
④ 極力曖昧な表現をしない説明
を示しています。
イマイチ成績が突き抜けられない受験生に貴重な情報が提供できればと思いますm(__)m
私の公式LINEでは無料相談を随時受け付けております。公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってください✊
私も苦手科目は先生に頼りました。
また、LINE登録していただいた方には、無料プレゼント(1年で偏差値70出す画期的勉強法)を贈呈します🎁
無料相談もどしどし受け付けております✊
【⬇️公式LINE登録はこちら⬇️】

阪大理系数学の特徴
阪大の理系数学は全5問で150分。10年前なんかと比べるとだいぶ穏やかなセットになった気もしますが、京大よりは東大寄りの難しさがありますね〜😇
去年はここ5年の難易度を考えると、やや難しめでしたが、やはり昔よりはやや易しめ。
今年はどんな難易度,出題内容だったのでしょうか🤔
第1問

難易度:やや易〜標準
【解答】



<分析>
まずzを用いて円を表す式(①)を立て、さらにzをwを用いて表します(ここでw≠1に注意!)。
③の形が出たら、r=1/2とr≠1/2で場合分けしていますが…これは、両辺2乗した際に|w|²が消えるか否かで表す図形が変わるからですね☝️
r≠1/2のときの計算が煩雑ですが、方針は明確なので、頑張って解き切りたいところ🤥
<感想>
頻出の、複素数平面の数式を変形する問題です。演習経験が多い受験生は、方針に迷うことはなかったでしょう。
本問のポイントは、w≠1を示すこと、r=1/2での場合分けですね☝️
第2問

【解答】
(1) 易
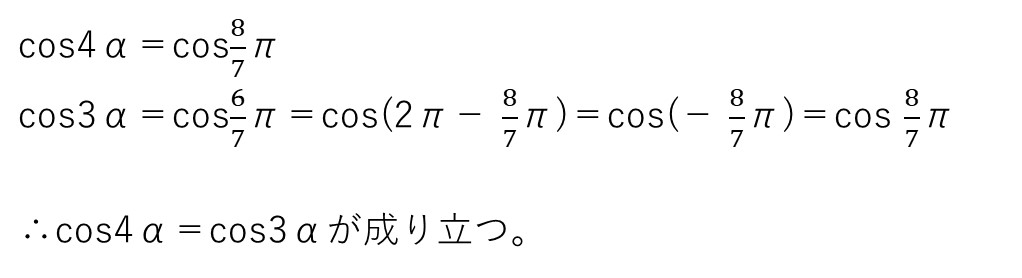
<分析>
cos8π/7とcos6π/7は、cos8π/7=cos(−6π/7)より、値が一致することはすぐにわかるでしょう。
(2) やや易〜標準

<分析>
f(cosα)の表示より、(1)の等式をcosαを用いて表すことを考えます。
cos4αは2倍角の公式より、cos2αを使って表せますが、さらにcos2αをcosαで表します。
cos3αは3倍角の公式よりcosαで表せます。以上よりf(cosα)=0が成り立ちます。
(3) 標準

<分析>
無理数を直接示すのは困難なので、有理数と仮定して矛盾を示す「背理法」がセオリーです☝️
解法もごく一般的で、特に詰まることはないでしょう。
<感想>
(1)はcosの性質を使えば簡単です。
(2)は(1)の等式をcosαだけで表せば、f(cosα)=0が導かれます。
(3)は背理法だな!と思えれば勝ちです✊
第3問

難易度:標準〜やや難
【解答】
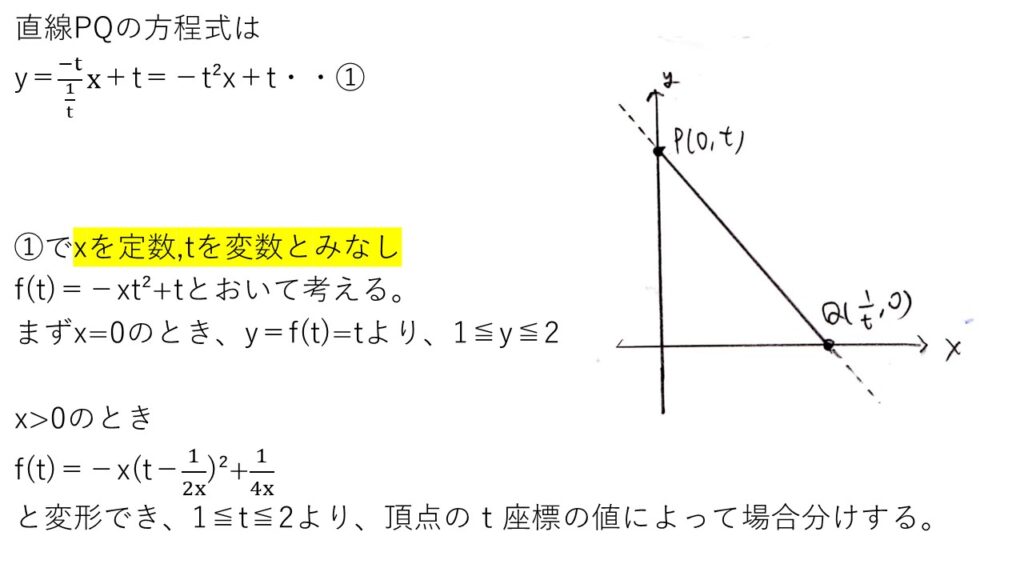
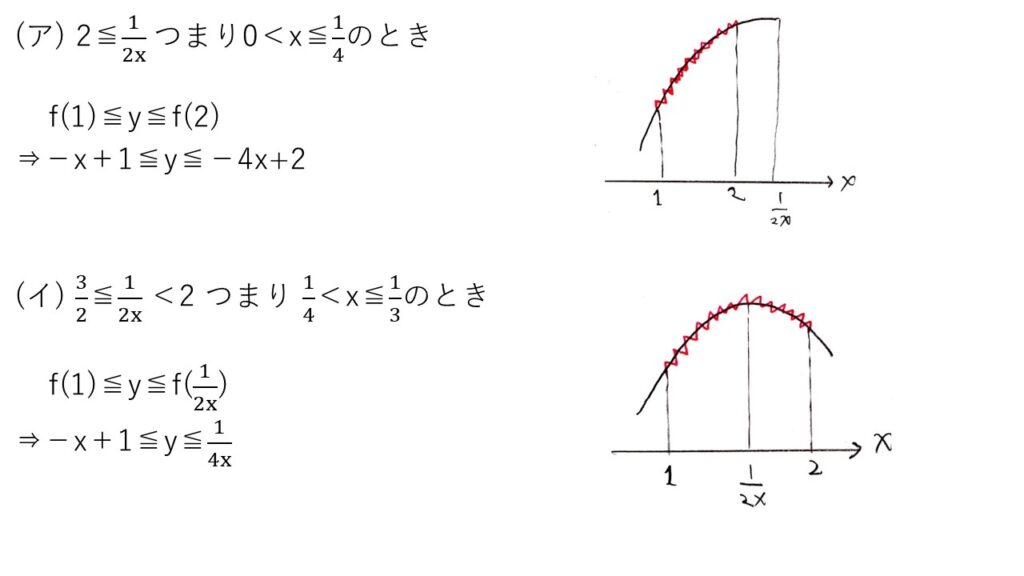
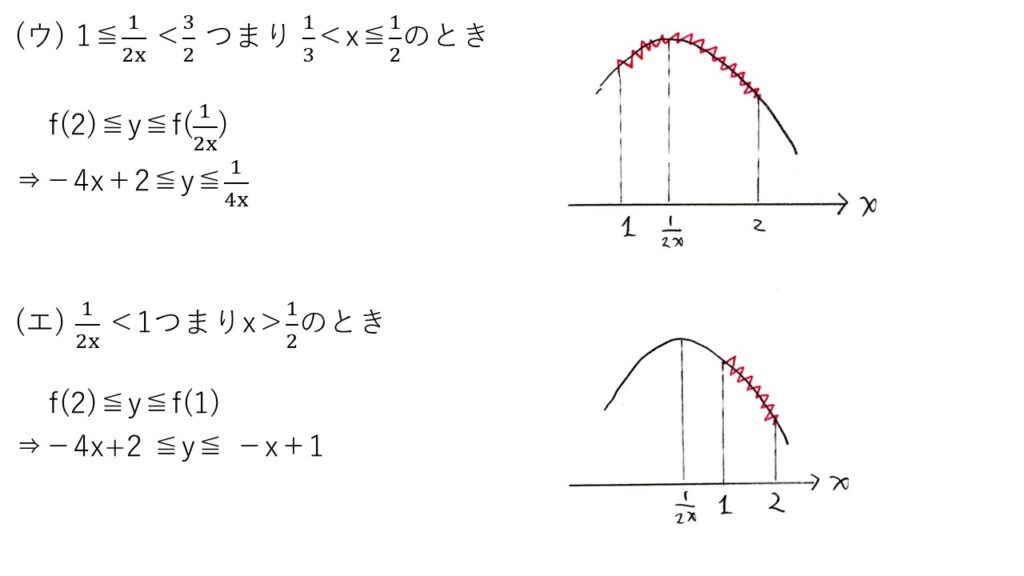
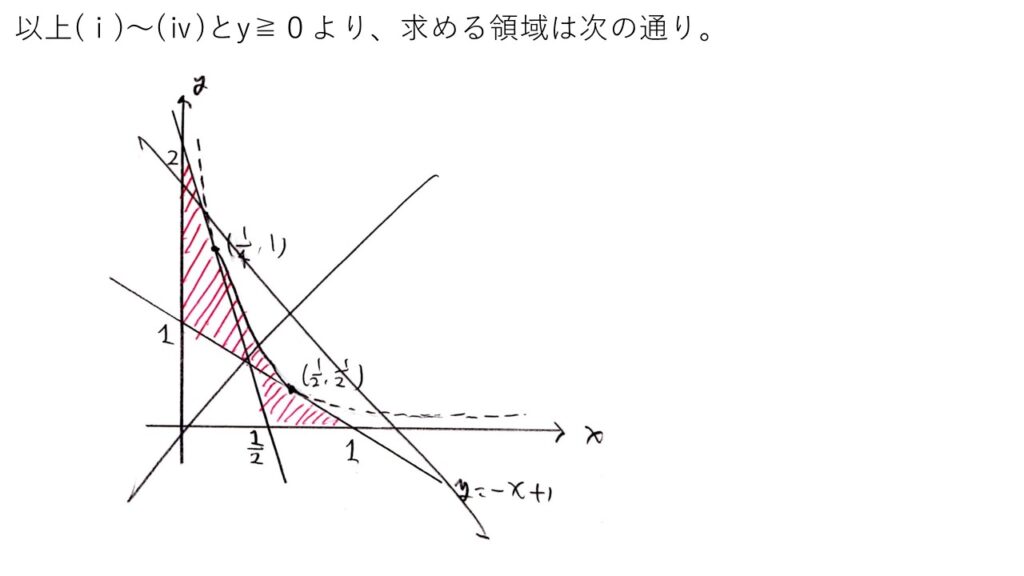
<分析>
直線PQの式を求めて、(x,y)を第1象限(x=0,y=0を含む)の点とyをxでなくtの関数(f(t))とみなします。f(t)は2次関数であり、1≦t≦2の範囲に頂点のt座標が入るかどうかで場合分けします☝️
<感想>
変数の視点を変えるのは、難関大学では定番の解法です。
本問でもxでなくtを変数と考えたのは、xの範囲は不明(与えられていない)なので、範囲がわかっている(1≦t≦2)tの方が扱いやすいと判断した結果です☝️
第4問

【解答】
(1) 易〜やや易

<分析>
定番の「差をとって微分」で解けます。ただ1つの解をもつことを示すには、単調増加(減少)性が示せれば簡単でしょう。
最後にg(1)>0と十分大きいxでg(x)<0を示すのを忘れないように!
(2) 標準

<分析>
中辺が何を表すか考えてみると、点(x,f(x))と点(α,f(α))を通る直線の傾きですね。
また、分子のf(α)をαとみなすと、中辺について平均値の定理が使えます。ここで、x<c<αですね。
f'(x)=1/x+1の形より、f'(x)はxが増加すると小さくなりますから、f'(c)<f'(x)が言えるのです。
(3) 標準

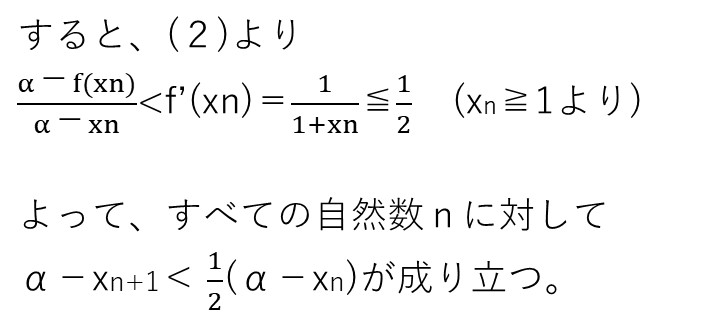
<分析>
1≦xn<αはわかるでしょうけど、勘はダメですよ…これを数学的帰納法で示す必要があります。
示せたら、(2)と同様に平均値の定理を用いてf'(xn)<1/2を示せばOKです🙆♂️
(4) 易

<分析>
これはサービス問題。お馴染みの「はさみうちの原理」ですね☝️
(3)が解けなくても、示したという前提で解きましょう!
<感想>
(1)はマトモな阪大受験生なら取りましょう。
(2),(3)は「平均値の定理を使え」なる誘導がなく、f'(x)の単調減少性を自分で示す点で、少し難度を上げていますが、これも演習経験があれば決して難しくありません。
(4)は見るからに、はさみうちです✂️
第5問

難易度:標準~やや難
【解答】

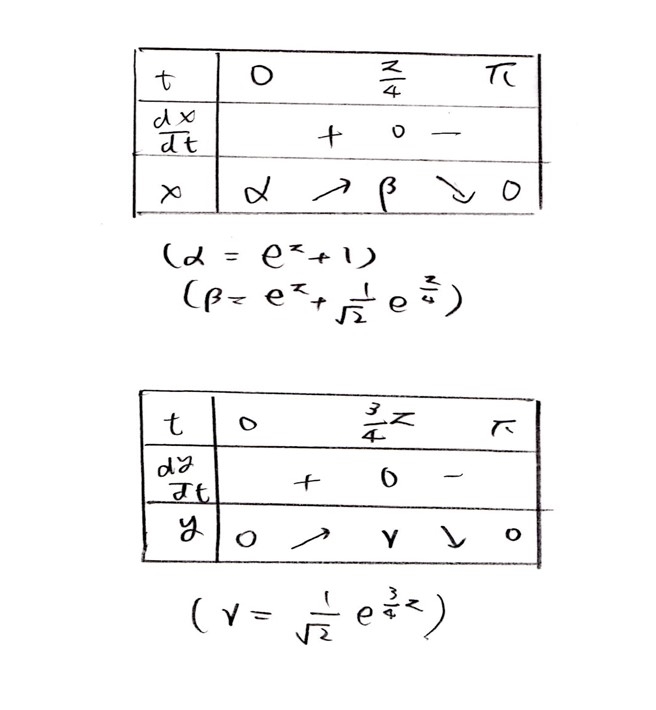
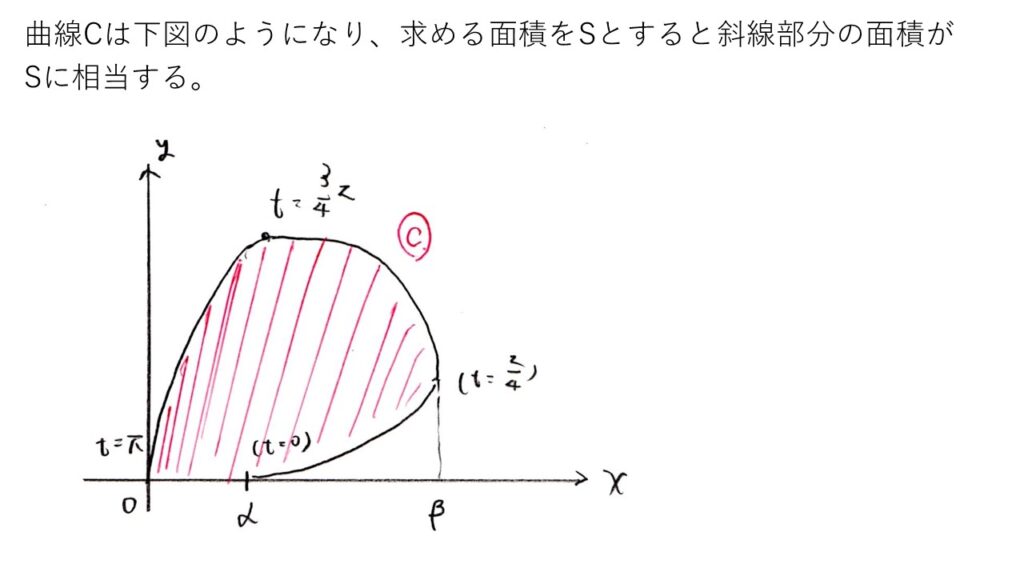
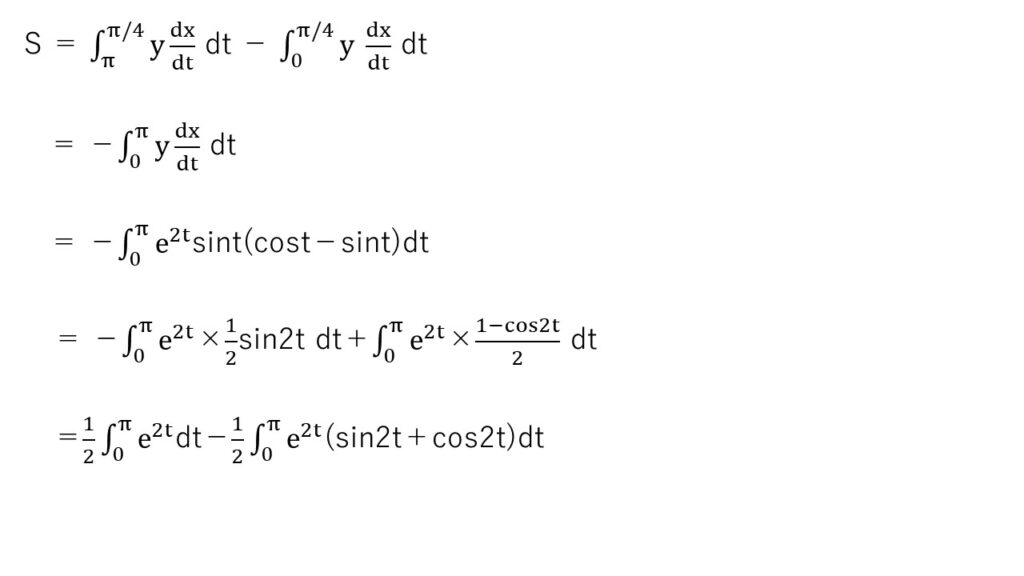
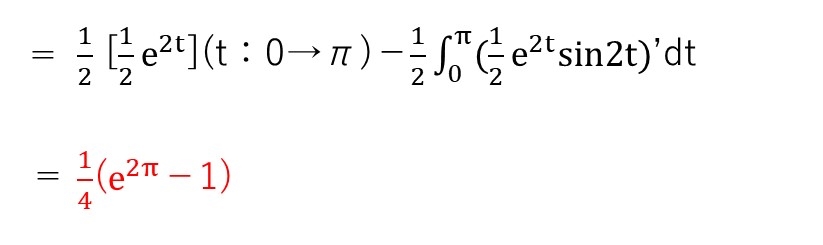
<分析>
0≦t≦πより、y≧0は明らかです。まずは定石通りにdx/dtとdy/dtを求めて、増減表とグラフを書きます。
xはβで増加から減少に転じるので、そこを境にyをy₁とy₂に分けて積分する訳です。
ここで、dx= dx/dt × dtを用いるのは大丈夫ですかね??
<感想>
(x,y)が媒介変数tを用いて表されるときは、微分して増減チェックが鉄則でした✊
そして、グラフが途中で折れ曲がるときは曲線を分けて考えるのでしたね💡
数Ⅲの面積問題では定番なので、解法がわからなかった方は、これを機によく身に付けておいてくださいm(__)m
総括
去年に比べると、文句なしの易化!第1〜5問すべてがどこかで見た解法で解けるものでした。
満点の難易度は低めなので、実力者は満点も全然狙える内容です💡
合格点は
非医:55〜60%
医:75〜80%
くらいでしょう。
最後に、再度公式LINEの紹介をします。
公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信する公式LINEはこちら👇
登録していただいた方には、無料プレゼント贈呈🎁の他、無料相談も受け付けております。





