東大合格者が2022年名大理系数学を徹底解説！｜ハイレベル理系大学受験講座　

2022年大学入試、旧帝大の第４弾は「名古屋大学」です。

当ブログの解説記事は、読者の成績を最難関レベルまでグングン伸ばすことを目標にしており、読者が必死に３年間努力すれば東大(理三以外)・京大(医以外)・九大医レベルに80％以上の確率で合格できることを目的に作成しています✊

市販の問題集のように、解法を丁寧に示すだけではありません！多角的なアプローチで問題を解きほぐしています✊

しかし、扱う内容はハイレベルなので、全くの初心者が手を出しても収穫は得られません。

① 各問の難易度
② 他分野や一般常識との関連事項
③ 問題の躓きポイント
④ 極力曖昧な表現をしない説明

を示しています。

イマイチ成績が突き抜けられない受験生に貴重な情報が提供できればと思いますm(__)m

you tube動画でも入試問題の徹底解説をしております。ブログ記事との相乗効果で深く理解でき実力アップに繋がること間違いなしでしょう☝️

(第１問)

(第２問)

(第３問)

(第４問)

名大理系数学の特徴

名大の理系数学は150分で4題です。東大や京大が150分で6問なのを考えると、「少なっ！」と思った受験生も多いでしょう…確かに時間的余裕はある方ですけど、九大,東北大なんかよりは1問1問が重いのです🤥💦

また、第４問がクソ難しいというのも名大理系数学の特徴の1つ‼️去年の第４問はまだ穏やかでしたけど💦

さあ、今年の第４問はどうだったんでしょうね😏

第１問

【解答】

(１) 易

＜分析＞

筆算形式でただ計算するだけ。めちゃ簡単🤥

(２) やや易

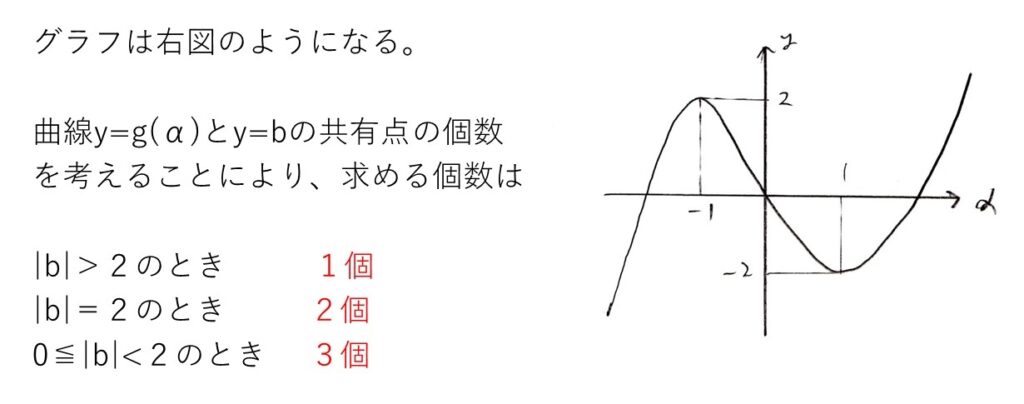
＜分析＞

(１)と同じ要領で割り算をすると、余りは(α2−β)x＋αβとなります。これが3x＋bに相当するので、2つの関係式が出ます。

αが定まればβが1つに定まるので、2つの関係式よりβを消去して、(αの3次関数)=bの形に持ち込めば、あとは3次関数の典型問題に帰着します👀

＜感想＞

第１問は簡単な問題が多いとはいえ、これは簡単すぎでは😅❓

(1)は高1でも解ける、(2)は3次関数のグラフとy=bの交点の数に帰着という、標準問題を固めていれば楽勝レベルの難易度でした🤥✊

第２問

【解答】

(１) やや易〜標準

＜分析＞

abの値は候補が多そうなので、c(1≦c≦6)の値について場合分けして考えましょう🤔そして、条件を満たす(a,b)の組数を求めていきます。

そもそも、ab+2≧abcが成り立つにはc≧2のときabはある程度小さい値に限定されますからね。

(２) 標準～やや難

＜分析＞

(１)のabcが2abcになったことに着目しましょう👀

何で2abcなの？て感じですが、2abcは偶数ですよね。なので、abは奇数でないといけません。ab=奇数に気付けば楽勝か～、と思いきや、

＜感想＞

(1),(2)とも似たような問題でした。ただ、求めている力が違います。(1)はcが大きいとabが限定されることに着目し、c=1〜6について調査。

(2)は2abcが偶数だからabは奇数と発想できたかがkeyでした🔑

第３問

【解答】

(１) 標準

＜分析＞

β/αを求めてほしいので、4α2−2αβ+β2＝0の両辺をα²で割ると何か見えてきそうですね🤔実際に、β/αに関する二次方程式となります。あとは、偏角arg(β/α)=π/3と、α,βの絶対値の比よりα,βの表す頂点を確定します。これは実際に正六角形を描いた方が話が早いでしょう🤫

(２) やや難

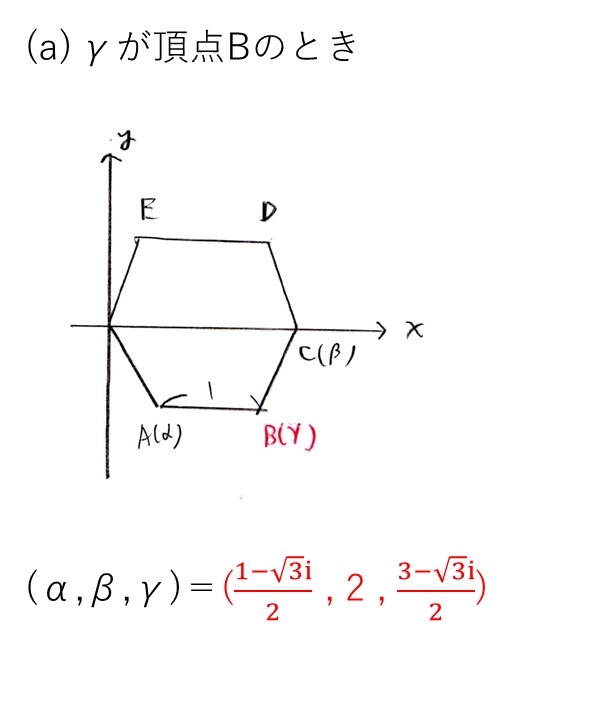
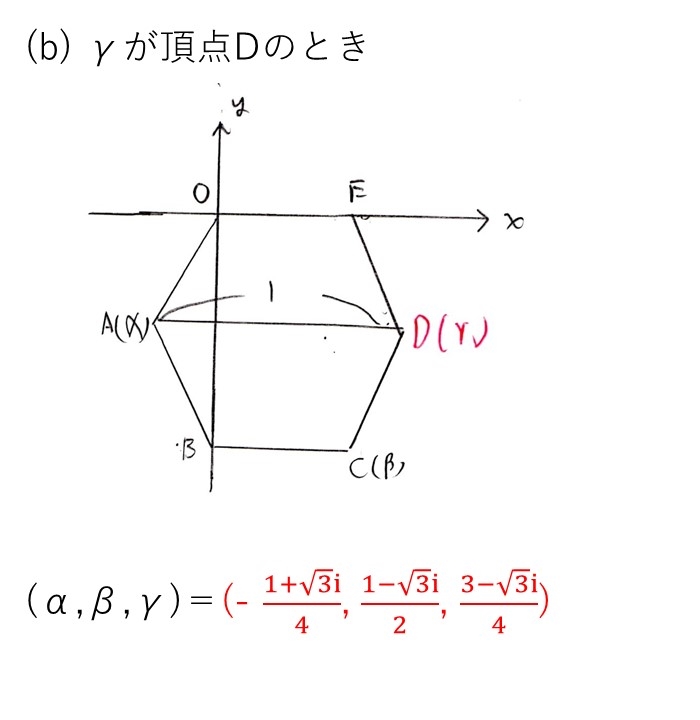
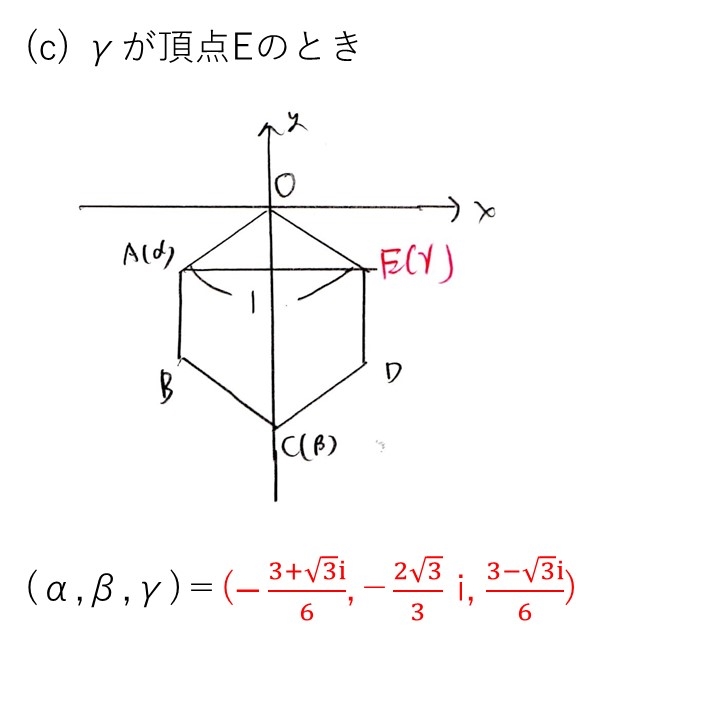
＜分析＞

(１)で扱わなかったもう1つの条件式を見ると、どうも因数分解できそうだな〜ていう雰囲気醸し出してますね！実際に因数分解すると、γ=α+1,α+β/2が出ます。

このうち、γ=α+β/2は2頂点の中心より不適なので、γ=α+1。あとは、γがどこの頂点にあるかで場合分けします。

＜感想＞

(１)は「β/αが求められる式はないか？」と考えれば、条件式の一方を使うのかな？と発想できたと思います。

(２)は因数分解の敷居はそう高くありません。難所は「γ=α+β/2を除くこと」「γがどの頂点にあるかで正六角形を描くこと」の2点でしょう。特に、正六角形を描く段階では、図形センスが問われています🤔