
受験生の皆さん、こんにちは。
東大合格ビジネスマンのワタシですm(__)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ 3大基礎力重視の裏ワザ勉強法
について、様々な観点から発信活動を行っております。
また、私の公式ラインでは無料相談を随時受け付けております。
公立中学出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、いち受験のプロの私に相談してみてください✊
私も、できない科目は先生を頼りました。
また、LINE登録していただいた方には
無料プレゼント(1年で偏差値70出す画期的勉強法)
を贈呈します🎁
【⬇️公式LINE登録はこちら⬇️】

2022年大学入試、旧帝大の第1弾は「北海道大学」です。
当ブログの解説記事は、読者の成績を最難関レベルまでグングン伸ばすことを目標にしており
読者が必死に3年間努力すれば東大(理三以外)・京大(医以外)・九大医レベルに80%以上の確率で合格できることを目的に作成しています。
市販の問題集のように、解法を丁寧に示すだけではありません。多角的なアプローチで問題を解きほぐしています✊
① 各問の難易度
② 他分野や一般常識との関連事項
③ 問題の躓きポイント
④ 極力曖昧な表現をしない説明
を示しています。
イマイチ成績が突き抜けられない受験生に貴重な情報が提供できればと思いますm(__)m
北大理系数学の特徴
北大の理系数学は120分で5問。全統記述模試と同じ時間配分ですね。
さて、今年の数学はどうだったのかというと
去年よりは全然むずいです!!
やっと骨太な問題を出してくれたぜ、北大🤣
でも、東大・京大志望者ならこのレベルで挫折する訳にはいきません。
第1問

【解答】
(1) やや易

<分析>
x<0および1<xのときにf(x)が最小にならないことに言及したいので、f(x)がx<0で単調減少、1<xで単調増加を示せばよいでしょう☝️
f(x)を直接求めてもいいし、第1項,第2項それぞれについて増減を調べてもいいです。
(2) 標準~やや難

<分析>
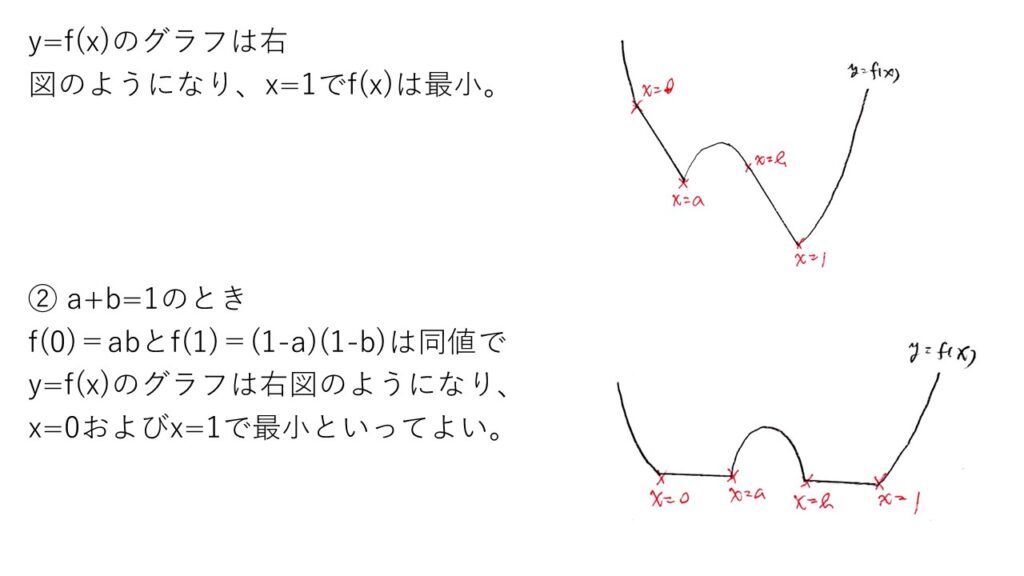
0≦x≦1でのf(x)の概形を調査したいですね👀
f(x)を求めると、0≦x≦aおよびb≦x≦1では直線、a≦x≦bでは上に凸の放物線であることがわかります。
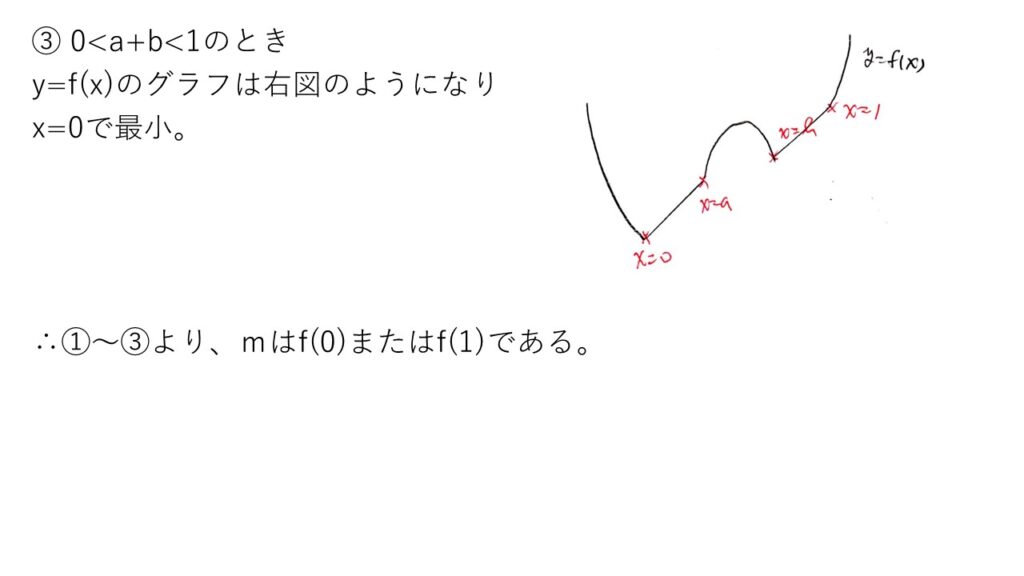
あとは1-(a+b)の正負で場合分けすれば、f(0)またはf(1)でf(x)が最小値をとることがわかるでしょう💡
(3) 標準


<分析>
f(0)=ab,f(1)=(1-a)(1-b)について、a+b=kとおくと、f(0),f(1)はaの2次関数となります。
あとは、この2次関数の最大値を調べることで解決できます💡
<感想>
(1)はまだ易しいので取りましょう✊
勝負は(2)以降です!受験には泥臭さも大事です。本問でも0≦x≦1の範囲で場合分けするのを面倒臭がるとできませんので、とにかく地道に調査です。直線と上に凸の放物線が出て、何となくf(0)かf(1)が最小なんであろうことは推測がつきますが、きちんと証明するのがやや難しいです💦
(3)は(2)で方針が見えればできるでしょう。a+b=k(0≦k≦2)とおき、場合分けしてかつbを消去する方針で示すと、結局a=b=1/2で最小であることがわかります。
第2問

【解答】
(1) やや易~標準

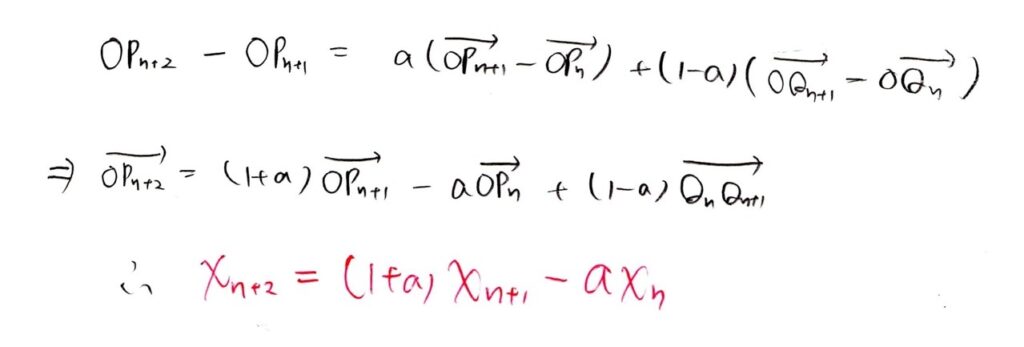
<分析>
求めるのはPn+2のx座標なので、まず条件式を原点Oを始点に変形することを考えましょう。
すると、OQnが出てきますが、ここで困ったことが発覚します🥲
そういや、 Q1のx座標わからんよね??
ここで、 QnQn+1が使えないか?と考えると、xn+2−xn+1を出す発想に至ると思います🤔
(2) やや易~標準

<分析>
(1)の漸化式を解けばOK!3項間の漸化式なので、特性方程式より2つの方程式が作れます。
あとは、an+1を消す方針をとればanが求められます☝️
(3) やや難



<分析>
(2)の過程がヒントになっています。yn+1−yn=Ynとおくと、Yn+1,Yn,a−nを含む漸化式作れますが、この類の漸化式の解法は難関大では典型的!
あとは、ynをΣ(シグマ)を用いて解くのですが、計算が結構厄介ですね〜🤥💦
<感想>
(2)は普通の3項間漸化式。(1)ができれば自動的にできる問題なので、(1)で躓くのは避けたいです。
(1)というか、条件式が与えられているベクトルの問題は、まず始点を原点に揃えて考えるのが王道パターンです👑
(3)は数列{yn+1−yn}を出す発想をできるかが第一歩です。また、「n乗を含む漸化式のは両辺を±n乗する」が鉄則でしたね。数列{yn+1−yn}が出たら、あとはシグマ(Σ)計算ですが、結構計算が汚く、計算ミスのリスクは高いでしょう😵💨
第3問

【解答】
(1) 標準

<分析>
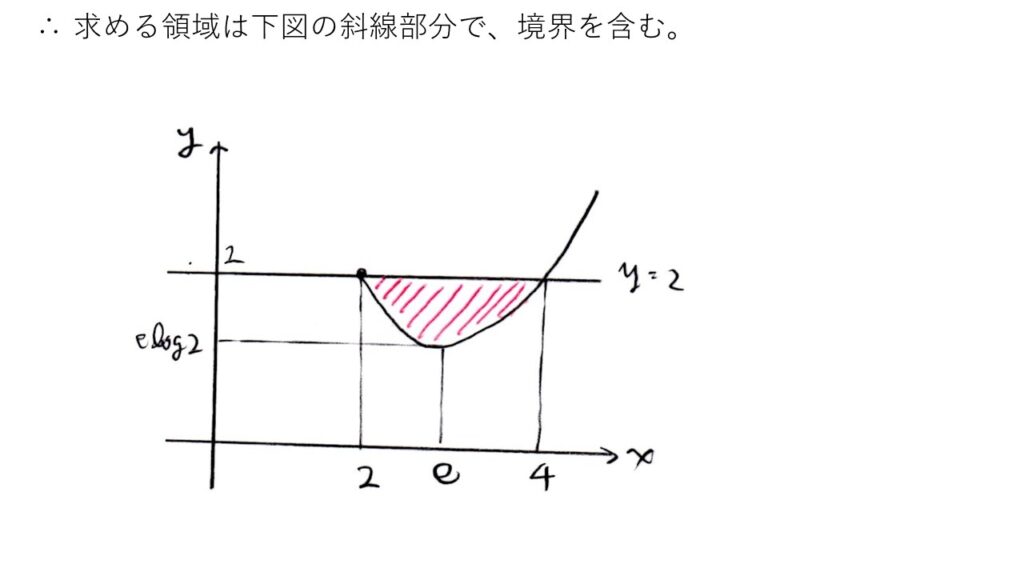
与えられたまんまの不等式ではyの範囲が不明なので、自然対数eのヒントもあることから、全辺eを底とする対数(log)をとると見通しが立ちやすいでしょう👀
あとは、左辺の(log2)x/logxの増減を調べればOK!
しか~し!北大レベルを考えると、y=2とのもう1つの交点が何かわからずに躓いた受験生が結構いたと思います😵💔京大プレの過去問でもあったな~、x=4を自分で見つけてくるタイプの問題。
(2) やや難〜難



<分析>
これは今年のセット最難問で確定でしょう🤥
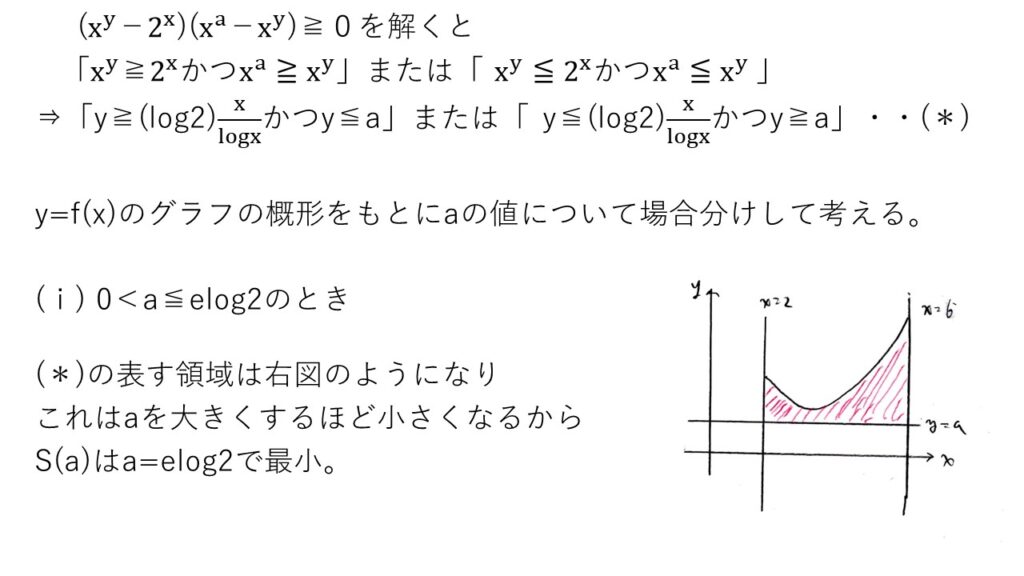
まずは、y=aがy=f(x)(2≦x≦6)と交差するときとしないときで場合分けします。
a≦elog2またはa≧6log2/log6のときは領域が単調に減少(増加)することを見抜き、計算を省きましょう。
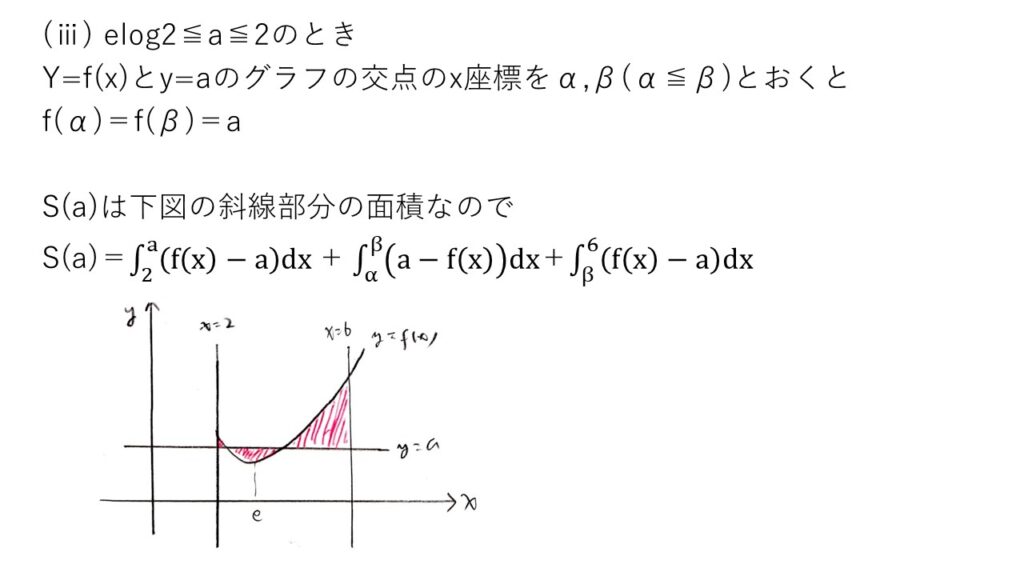
問題はelog2<a<6log2/log6のときです・・・これが大変‼️f(x)=x/logxを直接積分するのは不可能なこと、S(a)ではなくS(a)を最小にするaを求めればいいことに着目して、原子関数F(x)を準備する発想をしたかったですね💡
でも、馴染みがないと、この発想がまず難しい💔
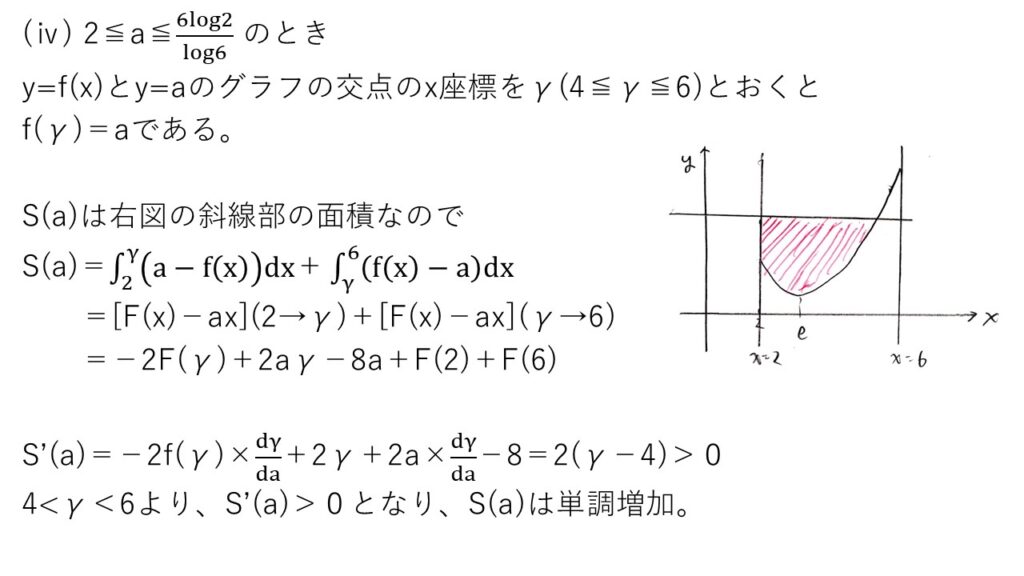
次に、F(a)を用いたS(a)の式をaで微分するのですが、dα/daが消えるのが見えないとパニックを起こしかねません。
<感想>
(1)はyの範囲がハッキリわかる不等式を出すことを意識すれば、累乗の形を外すべく対数(log)をとることが思い浮かぶでしょう🤔
(2)はムズイです。まずはy=aとy=f(x)が交差するか否かで場合分けすれば、aがすごく小さいときとすごく大きいときについては簡単に示せるでしょう。最悪、ここで部分点確保ですね💡
問題はこの後。S(a)を最小にするaを求めるのだから、S(a)を求める必要はありません✋
第4問

【解答】
(1) 易~やや易

<分析>
二次試験で円順列って何気に珍しい(笑)
本問は丸暗記でもできなくないですが、8個の異なるものを円形に並べるときの順列が(8-1)!=7!通りになるのはなぜか説明できることが大切です🤔
HOKKAIDOを例に出します(ここで,O,Kは区別する)。一列に並べた場合、HOKKAIDOとOKKAIDOHは異なりますが、円形に並べてHから読んだら・・・あら!同じになります💡KKAIDOHO,・・・,OHOKKAIDも同様です。なので、8!/8=7!通りになるのです。スッキリしましたか😂❓
(2) やや易

<分析>
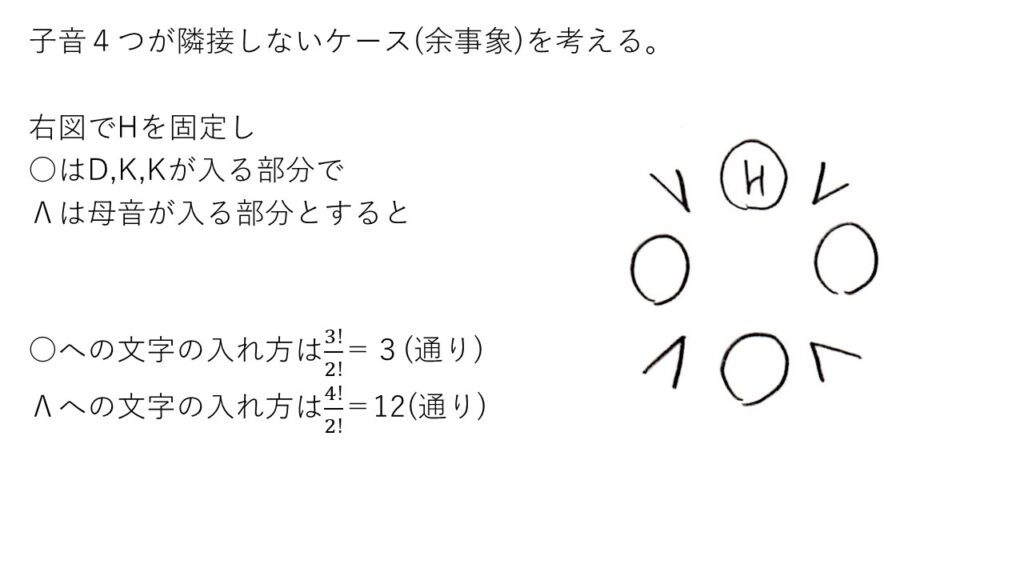
「3つとも隣接するのか?」「2つ隣接するのか?隣接するならどの組合せか?」・・・色々な場合分けが必要なことを考えると、直接調査がしんどいことは明らかです💦
そこで、困ったときの余事象を使います👍
余事象を求めて後で1から引けば、確率は出ます!なお、場合の数絡みの問題では、解答のように○やΛを使うと便利かつ簡潔に示すことができます💡
(3) 標準

<分析>
条件付き確率の問題ですね。「それ何?」となった方は、まず定義を覚えてからです💦
<感想>
円順列で思考停止した人は不合格街道まっしぐらだったでしょう💀
(1)は円順列の総数が出れば楽勝です。1/(総数)すればいいだけなんで。(2)では「困ったときの余事象」を使いましたが、忘れた頃に登場するので、今後もよく意識しておきましょう👍
(3)は(2)と逆に、連続しても問題ない子音を先に考えました。これ母音を先に考えると間違うリスクが高いです💦
第5問

【解答】
(1) 易~やや易
<分析>
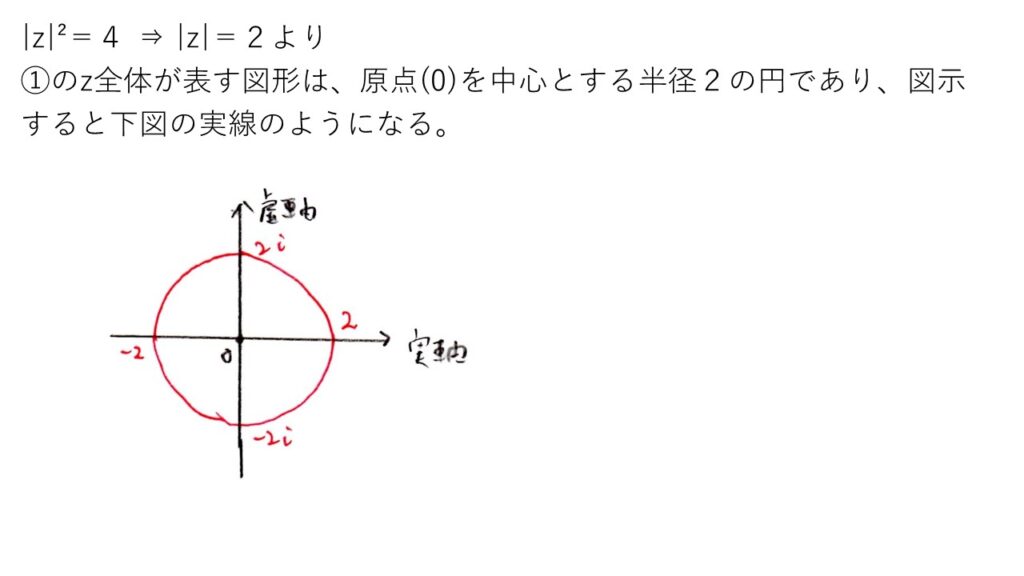
①は楽勝。できないと旧帝大受験失格です😮💨
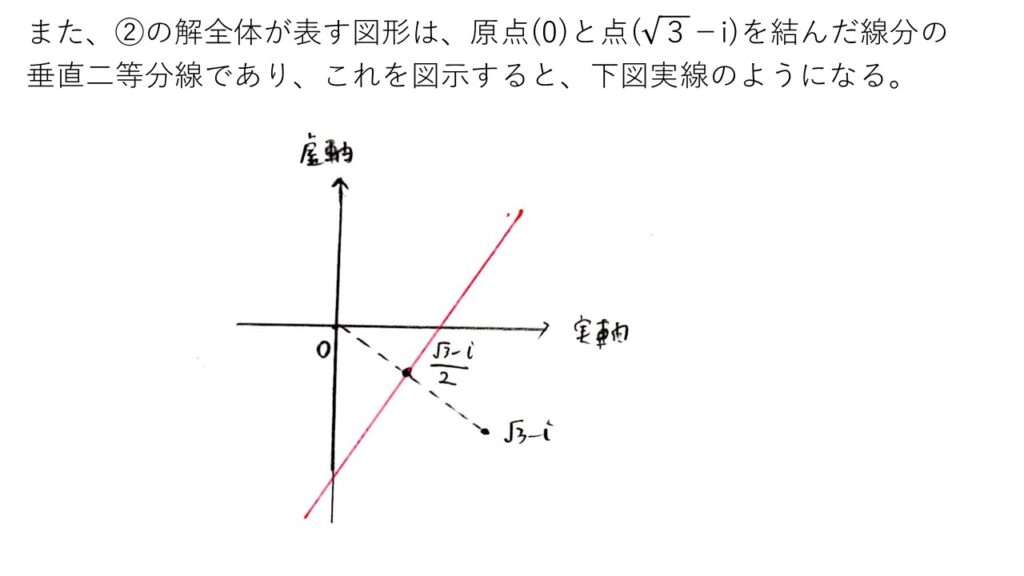
②はド忘れしてできなかった受験生もいたかも?そんな時は式の意味を考えましょう🤔
②は|z-0|=|z-(√3-i)|と変形でき、これは(zと0の距離)=(zと√3-iの距離)を表します。よって、2点を結ぶ線分の垂直二等分線が答となります☝
(2) やや易
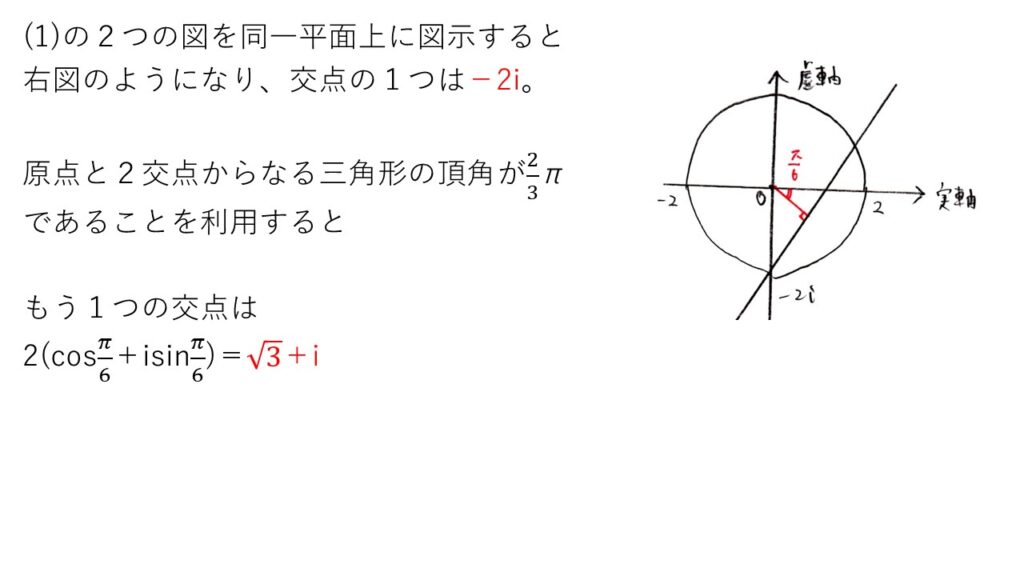
<分析>
実軸と0と√3−iを結ぶ線分のなす角に着目すれば容易に求められたでしょう。とはいえ、最悪xy座標の考えに持ち込んで直接求めることもできますが💦
(3) やや易~標準


<分析>
基本事項の組合せで全然難しくないです。
複素数でn乗ときたら、ド・モアブルの定理の出番です✋なお、n乗して偏角がθ→nθになることは数学的帰納法と加法定理で簡単に示すことができます。
<感想>
何気に(1)の垂直二等分線が合否の分かれ目だったかも💦
(1)ができれば、あとは共通テストで出てもおかしくない内容なんで、マトモな北大受験生なら完答したいところ。
総括
今年の北大は前半に重い問題が並びました。第4,5問は完答難易度が比較的低いものの、前3問で意気消沈して力尽きた受験生も多くいたことでしょう😵
完答難易度は3>>2=1>>4>5でしょうか。4も5も完答のしやすさは同じくらいですが、場合の数苦手な人多そうなんで💦
数学強者的には、2は重い計算をクリアすれば、1は場合分けと愚直な調査を面倒くさがらなければいけるかな~という感じです。
合格点は
非医:45~50%
医:65~70%
ですかね🤔
8割だと医学部でも断然有利でしょう。
では、以上で解説を終わります。
最後に、再度公式ラインの紹介をします。
私の公式LINEでは、無料相談を随時受け付けております。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってみてください✊
【⬇️公式LINE登録はこちら⬇️】





