2022年大学入試、旧帝大の第７弾は「京都大学」です。
当ブログの解説記事は、読者の成績を最難関レベルまでグングン伸ばすことを目標にしており、読者が必死に３年間努力すれば東大(理三以外)・京大(医以外)・九大医レベルに80％以上の確率で合格できることを目的に作成しています✊
市販の問題集のように、解法を丁寧に示すだけではありません！多角的なアプローチで問題を解きほぐしています✊
しかし、扱う内容はハイレベルなので、全くの初心者が手を出しても収穫は得られません。
① 各問題の難易度評価
② 他分野や一般常識との関連事項
③ 問題の躓きポイント
④ 極力曖昧な表現をしない説明
を示しています。
イマイチ成績が突き抜けられない受験生に貴重な情報が提供できればと思いますm(__)m
京大理系数学の特徴
京大の理系数学は全６問で150分。誘導も小問も少なめなので、all or nothingに分かれるリスクがでかいのが特徴ですかね🥲
ただ、20年前よりは全体的に簡単になっており、最近のセットでは、典型問題を幅広く押さえておけば2〜3完はできる内容となっています☝️
第１問
難易度：やや易
＜分析＞
log₁₀2が与えられているのが既にヒント💡まず底を10に直すことから始めます。次に、2048=2の11乗に着目して、log₄2022がlog₄2048=11/2=5.5より小さいことを示します。
続いて、2022よりなるべく近い小さい数で、かつlog10 2を使える数として2000を思い浮かべたいですね🤔
あとは、与えられた不等式を解答のように用いれば5.4より大きいことを示せます。
第２問
難易度：やや易～標準
＜分析＞
考え方は京大にしては簡単です。X,Y,Zのうちどれかを固定するとよさそうですが・・・例えばXを固定すると、Yと連動してZも動くことになりやりにくいですね💦
Xの代わりにYを固定すると、XとZの範囲がズバリ決まるので見通し良さそうです💡シグマ計算は少し煩雑ですが、完答しておきたい問題ですね☝
第３問
難易度：標準
【解答１】
【解答２】
＜分析＞
(解答１)では、n⁴+2,n⁶+2をn²+2で割った余りを考えることで、最大公約数が6の約数であると絞っています。
(解答２)では、(n⁴+1)−(n²+1)と(n⁶+1)−(n²+1)の両方に、n-1,n,n+1の連続3整数が含まれることに着目して、最大公約数を6の倍数に絞りました。
あとは、n=6k,6k±1,6k±2,6k+3で場合分けしてn²+2が6の約数(1,2,3,6)のどれで割り切れるかを調べれば答は出ます☝️
＜感想＞
(解法1)は河合塾の解答ですが、最大公約数をpなどおいて足し算,引き算する方がオーソドックスな解法なだけに、受験生的には(解法2)の方が思いつきやすい気がするのです☝️
連続3整数から偶数かつ3の倍数がいえるのはデカイですし。最悪、気合でn=8くらいまで調べて周期性を見出すのもアリでしょう。泥臭くても数学は答が出れば勝ち✊✊
解けそうだ！と思ったら、時にはゴリ押す気力も必要(笑)
第４問
【解答】
(１) 易〜やや易
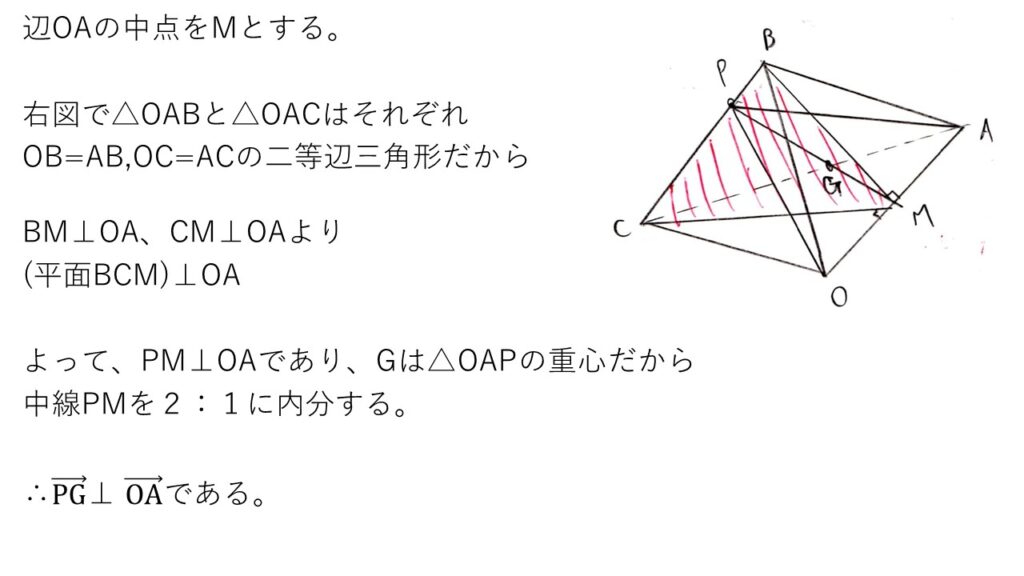
<別解＞
＜分析＞
前半は河合塾の解答ですが、幾何的性質から求めていますね。２垂線の存在から、平面BCMと線分OAが垂直だと言っています。
受験生的には、後半の解答のように、Oを始点とするベクトルで考えて、OP=kOB+(1-k)OCとおき、与えられた条件を用いて、kと無関係に内積＝０となることを示すのがオーソドックスな解法だと思います🙆♂️
(２) 標準
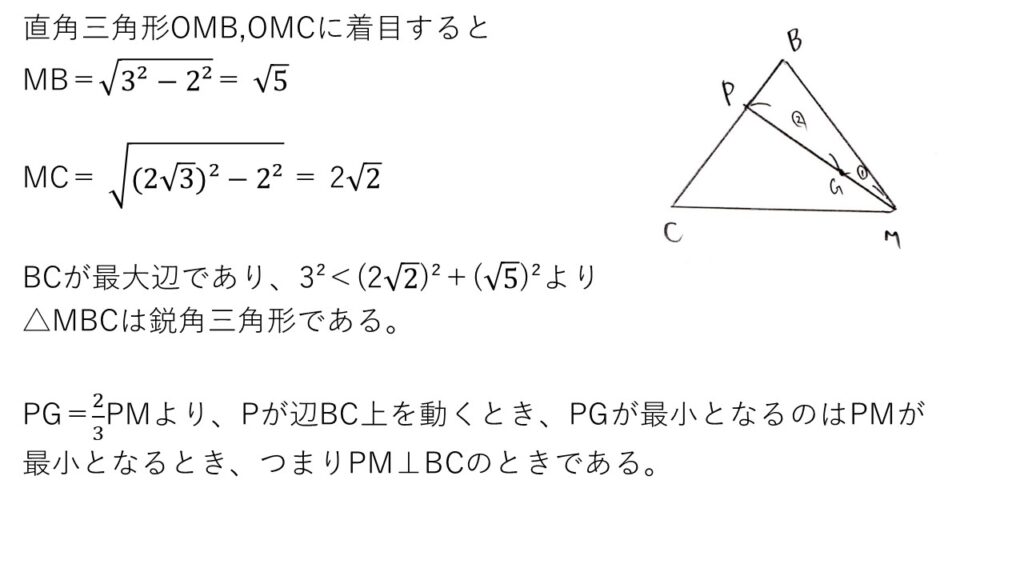
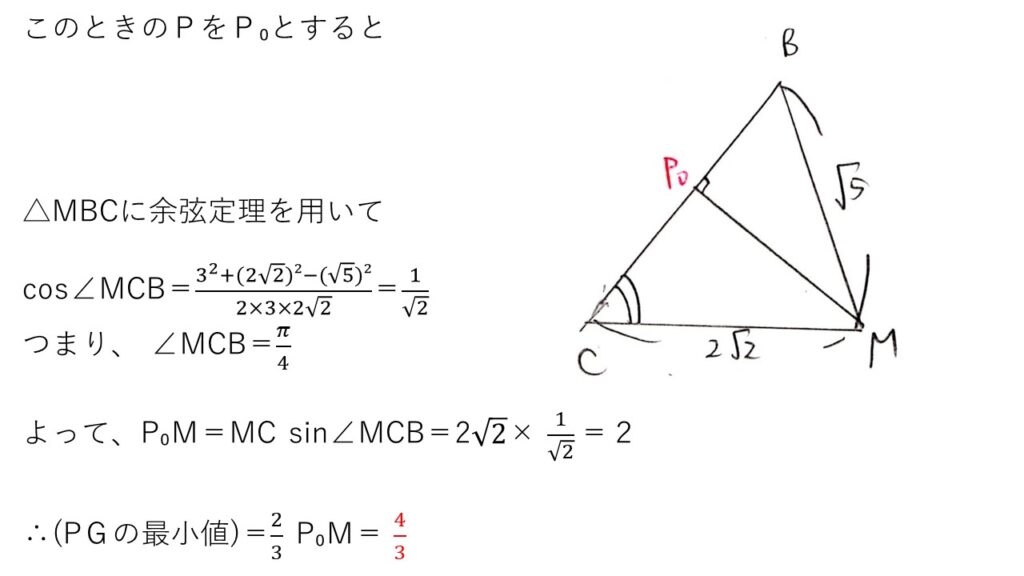
＜分析＞
これも図形的処理とベクトル計算の2通りの解法が考えられます。
＜感想＞
スマートな図形的解法、ベクトルでゴリ押す解法…どちらでも解けるなかなか秀逸な問題だったと思います🤔
京大らしい問題とはいえ、難易度的にはやはり2000年頃よりは易しいですね。
第５問
【解答】
(１) やや易
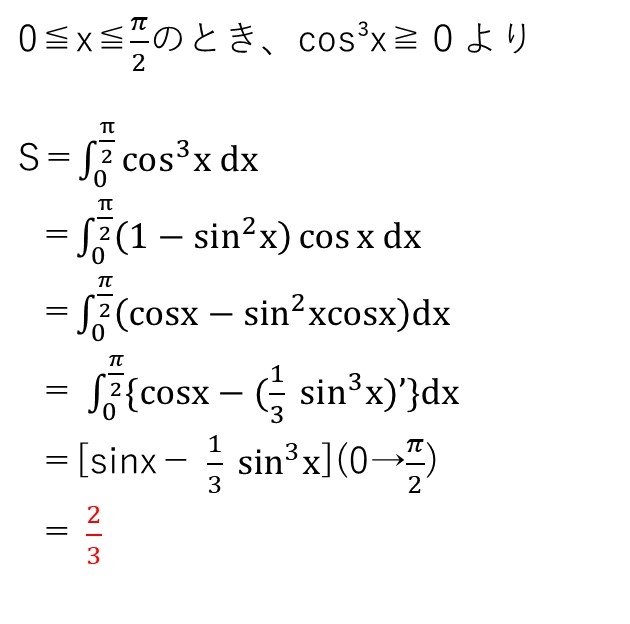
(別解)
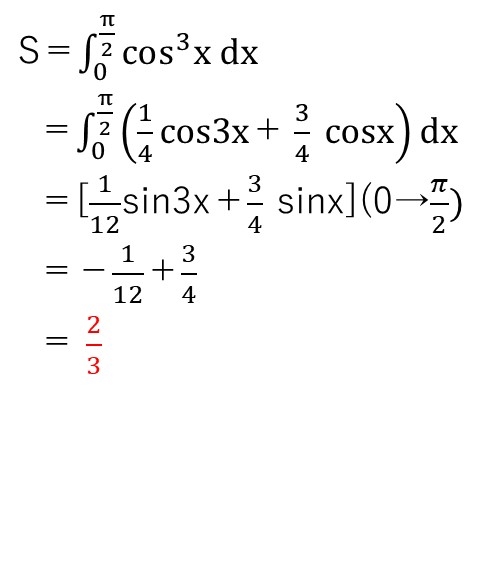
＜分析＞
cos3乗の積分は2通りの解法があります。1つは解答のようにsinを共存させる方法、もう1つは3倍角の公式を用いて累乗を消す方法です。
とはいえ、マトモな京大受験生なら経験済でしょうから、できてほしい問題です☝️
(２) 標準
＜分析＞
f(t)はすぐ出せますし、「最大値をただ1つ」の表現からf'(t)の単調減少性を示すのだろうと推測できます。なので、方針は立ちやすいですね☝️
あとは、答の形とf'(α)=0より、αをsinα,cosαを用いて表せばOKです🙆♂️
(３) 標準〜やや難
＜分析＞
(１)の結果を用いるとf(α)<3/8を示せばOKでしょう🙆♂️
今度は、f(α)をαの関数と考えて0<α<π/2よりf(α)が単調減少することを見抜きます👀
では、3/8がどこから出てくるか？ですが、これは多少発想力が要りますね〜。有名角としてはπ/6,π/4,π/3がありますが、このうち「sinαでルートが出ないのはどれか？」に着目すると、α＝π/6で調べれば良さそうだな？と思えるでしょう🤔
＜感想＞
とても標準的な数Ⅲの積分です。(3)でα=π/6を代入するのは多少発想力を要しますが、後は典型的な方針ですね👀
計算もやや穏やかなので、数学で稼ぎたい受験生はここは完答を目指したいですね☝️
第６問
難易度：やや難〜難
【解答】
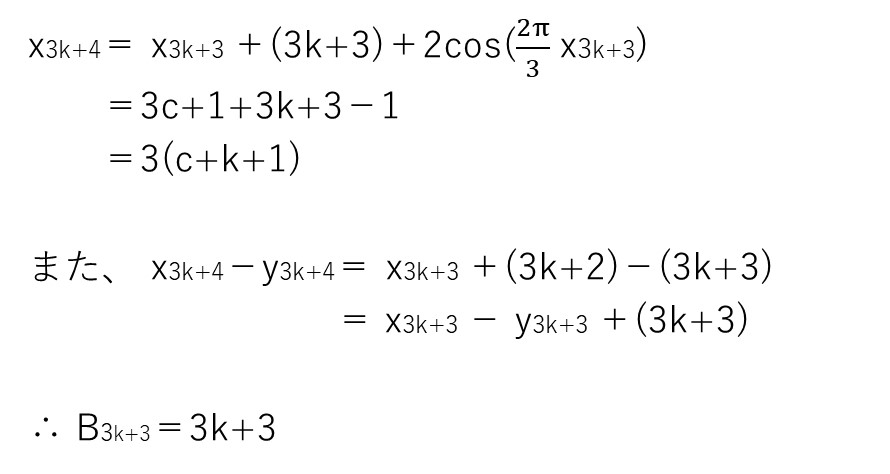
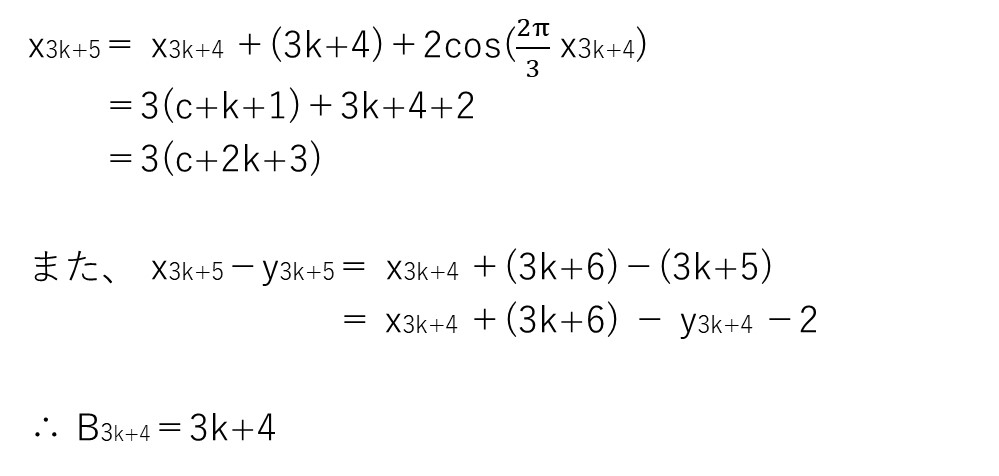
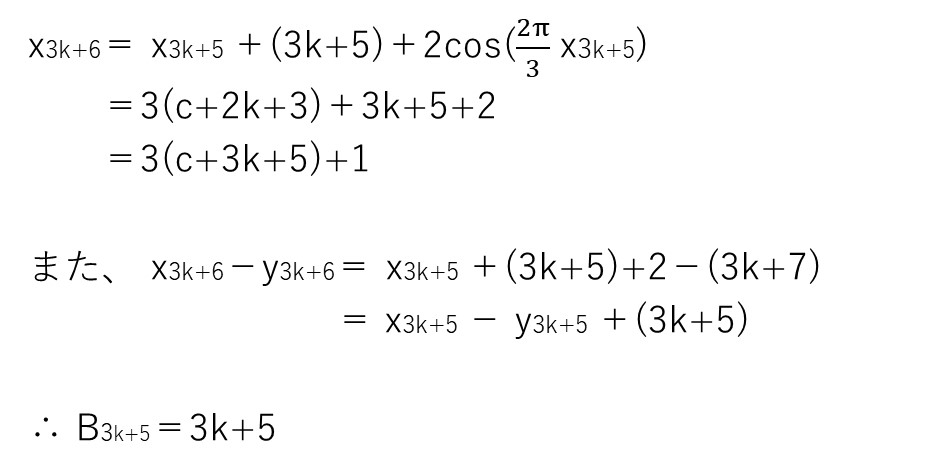
＜分析＞
与えられた漸化式をいじくったところでxnが不明なままだとcosの値も不明…つまり、式変形は意味を為さないと思われます。
そこでどうするか？ですが、ここは泥臭く調査に踏み切りましょう🔍
解答ではn=1〜6まで泥臭く調査してますが、どうやら「xnを3で割った余りに規則性がありそう」で「xn−ynの階差数列がnになりそう」ですね🤔これが見えたら、後は数学的機能法でゴリ押して終了です✊
＜感想＞
漸化式絡みで式変形できそうにないタイプは、小さいnで実験して規則性を見出すのが鉄則です✊
本問もなかなかいい味出してましたね〜🤤実験で2つも規則性見つかるとはね！
総括
今年は第１〜５問は京大にしてはやや易しいセットでした。しかし、第6問は気付かないとall or nothingになりうる京大らしい問題でしたね！
とはいえ、第6問の難易度は去年よりマシです。意外にも、医学科志望で合否を分けたのは第６問かもしれません🤔
合格点は
非医で55〜60%
医で75%前後
でしょうか🤔
医学部受験ブログランキング、家庭教師ブログランキングに参加中。ブログ活性化にご協力ポチッとよろしくお願いします🙇♂️
href=”https://juken.blogmura.com/juken_medicalschool/ranking/in?p_cid=11106032″ target=”_blank” rel=”noopener”>
にほんブログ村
にほんブログ村
