
受験生の皆さん、こんにちは。
東大合格ビジネスマンのワタシですm(__)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ 3大基礎力重視の裏ワザ勉強法
について、様々な情報を発信しております📢
私の公式LINEでは無料相談を随時受け付けております。公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってください✊
私も苦手科目は先生に頼りました。
また、LINE登録していただいた方には、無料プレゼント(1年で偏差値70出す画期的勉強法)を贈呈します🎁
無料相談もどしどし受け付けております✊
【⬇️公式LINE登録はこちら⬇️】
私の公式LINEでは無料相談を随時受け付けております。公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
2021年入試、旧帝大の第4弾は
「名古屋大学」です。
当ブログの解説記事は、
読者が必死に3年間努力すれば
東大(理三以外)・京大(医以外)・九大医
レベルに80%以上の確率で合格できる
ことを目的に作成しています
市販の問題集のように、解法を丁寧に示すだけではありません!多角的なアプローチで問題を解きほぐしています✊
① 各問の難易度
② 他分野や一般常識との関連事項
③ 問題の躓きポイント
④ 極力曖昧な表現をしない説明
を示しています。
イマイチ成績が突き抜けられない受験生に貴重な情報が提供できればと思いますm(__)m
名大理系数学の特徴
名古屋大学の理系数学が全4問で制限時間は150分。
同列の旧帝大と比べて1題がやや重いです。
東大や京大が6問であることを考えると、時間的余裕はまだあると思います😳
例年
第4問の完答難度が異常に高い
のが特徴です。
内容を深く理解するためには、素養として
全統記述模試で偏差値65程度
は欲しいですね✊
この大学ではご丁寧に「公式集」とか付いてくるんですが、ちゃんと勉強してきた受験生には正直要らないです(笑)
第1問

【解答】
(1) 易

<分析>
共通テストでも初歩的な問題。これはさすがに皆できるでしょう(笑)
(2) やや易~標準


<分析>
C₁の接線がC₂にも接する条件を求めると②が出ます。さらに「条件を満たす接線が2本ある」⇔「C₁の接点(t,t²)が2個存在する」に着目したいところでした👀
ここは、非医志望者で差が付いた問題と言えそうです💦
(3) やや易

<分析>
(2)の②が出せればできるので、(2)よりは簡単。
ℓ,ℓ’の交点の座標の対称式より、条件反射的に「解と係数の関係」が思いついてほしいところですね🤔
(4) やや易~標準
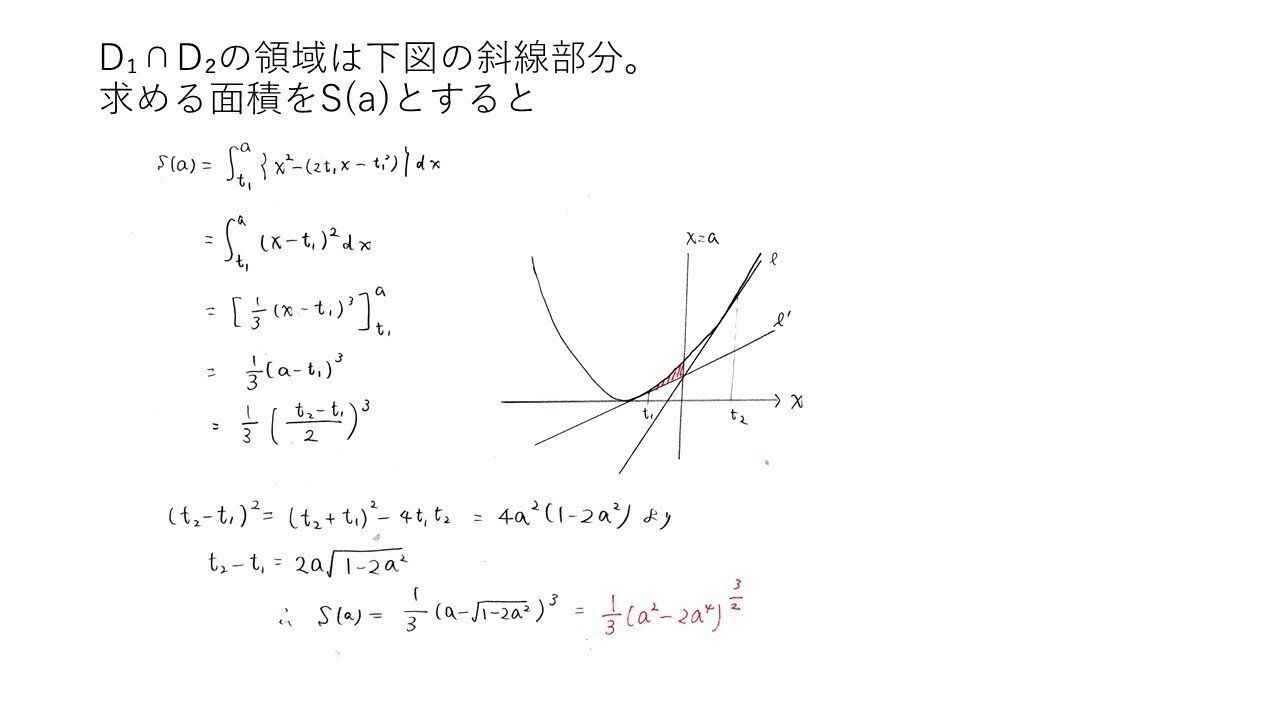
<分析>
S(a)の立式は何も難しくありません。しかし、最後の処理で手こずったかもしれませんね💦
(5) やや易~標準

<分析>
S(a)にa⁴,a²が含まれることから、a²について平方完成ができそうですね☝
平方完成して、S(a)が最大となるaが条件を満たすことをいえばできます。
<感想>
(1)~(5)まで小問多いな・・・と思いきや、簡単な問題の寄せ集めで至って普通でした。
合格を確実にするには完答を目指したい
ですね。
できなかった方は、(2)(3)でなぜその考え方をするのか、自分が納得できるくらいに理解しておきましょう✊
第2問

(1) やや易~標準

<分析>
直接比較が無理なのは明らかです。
底がバラバラなので、見通しを良くするためにも底を揃えましょう!
(2) 標準

<分析>
「logabでa>1のときb>aなら1より大」に着目します👀
すると、まずγは1未満であろうと見抜けますね!α,β,γについては差をとってチェックが最適でしょう。ここでも、(1)と同様に底を揃えます。
(3) 標準~やや難

<分析>
3次方程式の解と係数の関係とp=α+β+γに着目すると、(x+α)(x+β)(x+γ)=0がx³+px²+qx+1=0になりそうだ!と目星がつくでしょう👀
あとは、解を-α,-β,-γと特定し、3次関数のグラフを描いて、(2)で出た大小関係を使うのでしょう。
<感想>
底の変換(統一)が必要な問題でしたが・・・数学が苦手な方、対数の扱いがよくわかってない方は、下手したら(1)で躓いてしまいます😵
今回のセットでは最も出来不出来が分かれた問題ではないでしょうか💦
第3問

(1) やや易

<分析>
(b)より、石は右か下にしか移動しないことを読み取ります👀
もし3や6を選べば2には行けないですよね?よって、石は最初1か2にあるべきです☝
(2) やや難


<分析>
5で終了する確率をどう考えるかで明暗が分かれたでしょう💔
解法としては
①「最初1,2,3,4,5を出す場合に分けて考える」または
②「p₁,p₂,・・.p₅を求めて、石が2→5に行く場合等を考える」
という2通りの解法が考えられます🤔
しかし、①の解法は非常に面倒くさいので、②の解法に気付けたかが勝負でしょう💦
(3) やや難

<分析>
(2)ができれば完全におまけ。最後には5,9,11,12にいることから、p₉は余事象で出せますね!
<感想>
今回は漸化式系ではなく調査系ですかね?確率は一見道筋が見えないことも多いので、まず手を動かして調査する姿勢が大事ですね。
規則がわかれば難しくはないけど、(2)以降は調査が煩雑で差が付く印象。(3)は完全におまけ。(2)をクリアしてればp₁₂も求まるでしょう。
ゴリ押せば出せると確信したら、挑戦あるのみ!受験は一種の点取りゲームです。
学力のみならず、根負けしない精神力も非常に大事です✊
第4問

(1) 易

<分析>
a+1/2は「1/2以上3/2未満の値」をとるので、a=1/2を境に場合分けします。これは簡単ですね。
(2) 標準
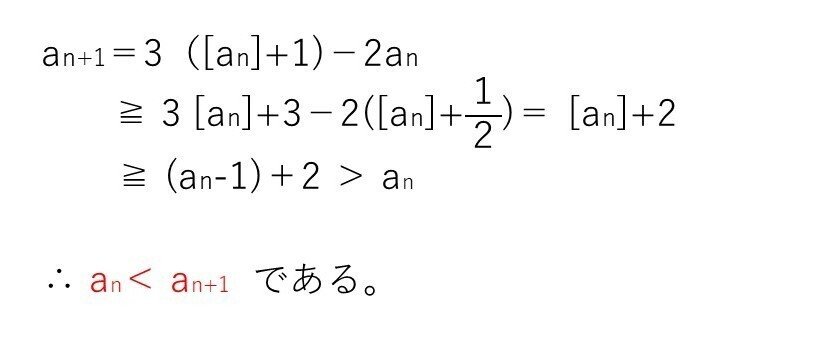
<分析>
少し難しいですかね💦
an-[an]≧1/2 ⇒ 「anの小数部分が1/2以上1未満」と解釈します。このとき
[an+1/2]=[an]+1
an≧[an]+1/2
だと気付けたでしょうか🙄
(3) 標準~やや難


<分析>
(2)の流れから、an>an+1でan-[an]<1/2かな?と推測できます。
また、整数部分,小数部分を一度M,mなどで置き換えるとスムーズに進んだでしょう。
(4) やや難


<分析>
漸化式が出てからの処理で経験の差が出たと思います。
左辺にan+1、右辺にanがいることから、-3nをn+1とnを含む式にバラして、左辺にn+1,右辺にnを含む形を作ることを考えましょう🤔
<感想>
第4問はガウス記号がきました。要は、実数xの整数部分のことです。
例えば、[16.3]=16、[3.01]=3ですね。ガウス記号も難関大学ではよく出るので、何かわからん人は1度確認しておきましょう。
(4)はnが混じる漸化式の変形がkey🔑でしたが、経験値で差が出ました。実は、nが絡む漸化式処理は「やさしい理系数学」の例題に出てますので、手持ちの方は確認しておいてください!
例年は第4問が超難問ですが
今年は影を潜め
8割以上の高得点を取る
難易度は下がりました😂
下手したら、第3問(2)が最難問だったかもですね。
第1問は完答が望ましい。
第2問は(2)まで取りたい。
第3問は、この手の数え上げが苦手なら(1)のみでも仕方ない。
第4問は(2)まで取りたい
という印象です🧐
合格点は
非医:55%程度
医:75%程度
でしょうか🤔
合否を分けた問題は
非医だと第2問
医だと第3問または第4問
でしょうか。
医志望で第3問を完答できれば有利ですが、無理なら第4問を沈めたいところです💦
最後に、再度公式ラインの紹介をします。
私の公式LINEでは、無料相談を随時受け付けております。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってみてください✊
【⬇️公式LINE登録はこちら⬇️】






