受験生の皆さん、こんにちは‼️
東大合格ビジネスマンのワタシですm(__)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ 3大基礎力重視の裏ワザ勉強法
に関する情報を、多角的な観点から発信しております📢
今日は短めです。
読者(受験生)の皆様は
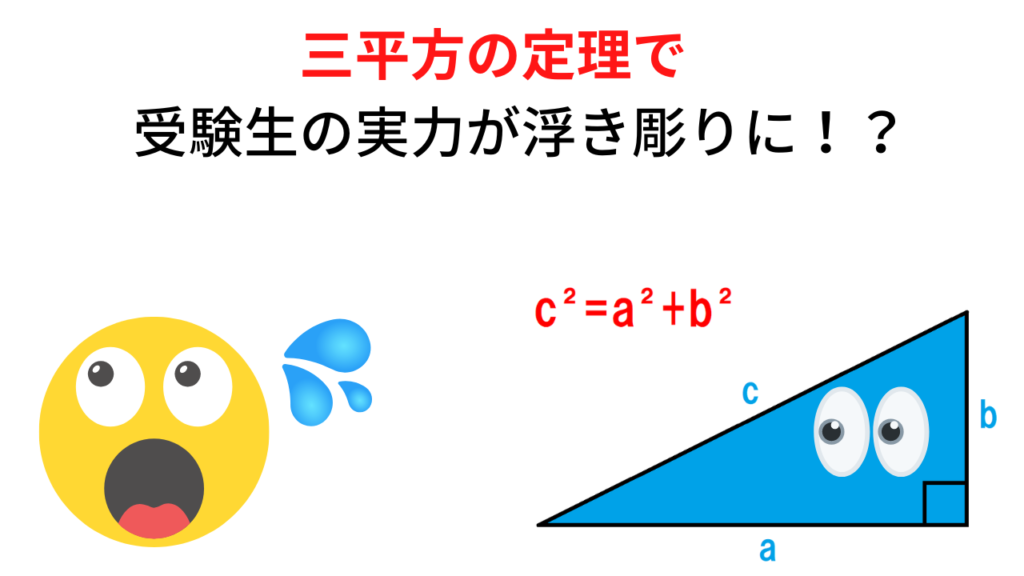
「三平方の定理」
からわかることを
できるだけ沢山説明してくれ
と言われたら、何と答えるでしょうか??
ちなみに
「三平方の定理」は
公立中学だと3年生の数学で習います。
高校生以上の読者の方なら
誰しもが
「それくらい聞いたことあるわ~」
と思うでしょうけど…
問題は
自身がどれくらい深く理解し
運用できているか
なのです。
これで、個人の学力が如実に判明してしまうのですm(__)m
you tube版はこちらです👇
私の公式LINEでは、無料相談を随時受け付けております。
公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってください✊
私も苦手科目は先生に頼りました。
また、LINE登録していただいた方には
無料プレゼント(1年で偏差値70出す画期的勉強法)
を贈呈します🎁
【⬇️公式LINE登録はこちら⬇️】

うまいことごまかしても
どんなに優等生ぶっても
わかる人には、あなたの立ち位置はバレバレです😭😭
三平方の定理(ピタゴラスの定理)とは、皆さんお馴染みのコレですね👇

覚えているか否かは別として
皆様、一度は聞いたことがあるはずです🙆♂️
以下では
・学力層別に推測される解答
・成績upに大事なエッセンス
を記載しています。
気になった方は
是非目を通してみてください👍
以下で
「三平方の定理に関連することを、できるだけ多く説明して?」

と聞かれたときの
様々な学力層から推測できる答を提示します。
調査対象は18~22歳程度の大学生。
一問多答式ですからね~
これで学力差が浮き彫りになります👀
もちろん実際に調査した訳ではなく、私が様々な経歴の方と接してきた経験談、自分が這い上がった過程を振り返って記述したものですm(__)m
1:高卒レベル
あ〜何か聞いたことあるな。
何やったっけ?
忘れたわ。
でも、仕事に必要ないし、将来使わんし
別にどうでもいいでしょ~🤪
2:Fラン大学
直角三角形で出てくるやつでしょ?
何かを二乗すんやったっけ?
でも、将来これ使うんか😇❓
3:無名国立大,MARCH
直角三角形で出てくる
a²+b²=c²
のことでしょ😀
受験生終わったし、もう使うことないよね。
4:旧帝大,地方医,早慶
直角三角形で90度を挟む辺の長さをa,b、斜辺の長さをcとすれば、a²+b²=c²が成り立つ定理よね☝️
ピタゴラスの定理とも言うね。
受験生時代が懐かしいねえ😌
5:東大,京大,旧帝医
(旧帝大,早慶)の答にプラス👇
そういや、余弦定理で左辺をcos90°にしたら右辺がまんま三平方の定理になるやん。
さらに、2乗は平方数て言うし、3つの2乗を使った式だから「三平方の定理」て言うのかもね💡
6:東大理三,京大医
(東大,京大,旧帝医)の答にプラス👇
面積の平方cm、√=平方根、二次関数の平方完成でも「平方」出てくるね。
2が絡むのは数学では平方と呼ぶらしい。そう考えると、3が絡むのは立方やね。
体積の立方cm、縦横高さが同じ立方体、3√=立方根と言うし。
やはり、三平方の定理を「三平方の定理」で終わらしちゃコスパ悪いよね🥵
他分野さらには他科目にもアンテナを張って、学習効果を上げる勉強法を追求するといいよ☝️
7:1~6の事例からわかること
以上の調査内容から、その方がどれだけ1つの分野について深く理解していて、他分野と関連付けて理解していて、かつ自分なりの考えを持っているかがわかるでしょう。
中3レベルの数学の一定理をとっても
学力差があると
答えられる量が全然違う
のです🤭💦
今回の「三平方の定理」は
ほんの一例にすぎません。
これが
数学の他分野
さらには、受験科目全般
に渡って起きているとすると
高卒の方でさえ
東大・京大を本気で崩しにいくのが
想像の100倍は難しいことが
推測できるでしょう🥵
(https://www.ac-illust.com/main/search_result.php?word=立ちはだかる壁より引用)
勉強量を蓄積し他分野にも意識を向けることで、様々な勉強に派生できるのを実感頂けたでしょうか🤔❓
東大理三余裕合格の神童も、わざわざ言わずとも、無意識下で完璧に理解しているでしょう。
そんなの当たり前だろ?
と思って口に出さないだけかも(笑)
先天的要素に加え、英才教育,進学塾,私立進学校などの周囲の環境、家庭の裕福度に左右される面も少なからずあるとは思いますが…
クラスのみんなと同じことやって成果が出ないのは、少なくとも先天的才能がないということなので
出し抜きたいなら
考え方や戦略に
独自性を持たせる努力
は必要になるでしょう🤫
本記事が
凡才で悩む受験生の皆さんに
役立てると幸いです🙇♂️
最後に、再度公式LINEの紹介をします。
公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信する公式LINEはこちら👇
登録していただいた方には、無料プレゼント贈呈🎁の他、無料相談も受け付けております。







