
受験生の皆さん、こんにちは。
東大合格ビジネスマンのワタシですm(__)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ 3大基礎力重視の裏ワザ勉強法
2022年大学入試、旧帝大の第3弾は「九州大学」です。
当ブログの解説記事は、読者の成績を最難関レベルまでグングン伸ばすことを目標にしており、
読者が必死に3年間努力すれば東大(理三以外)・京大(医以外)・九大医レベルに80%以上の確率で合格できることを目的に作成しています。
市販の問題集のように、解法を丁寧に示すだけではありません!多角的なアプローチで問題を解きほぐしています✊
を示しています。
イマイチ成績が突き抜けられない受験生に貴重な情報が提供できればと思いますm(__)m
私の公式LINEでは、無料相談を随時受け付けております。
公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってください✊
私も苦手科目は先生に頼りました。
また、LINE登録していただいた方には
無料プレゼント(1年で偏差値70出す画期的勉強法)
を贈呈します🎁
【⬇️公式LINE登録はこちら⬇️】

九大理系数学の特徴
九州大学の理系数学は全5問で150分。東大や京大が150分で全6問であることを考えると、多少時間的余裕はあるかと思います。
過去7年ほど見た感じ、計算量が東北や北海道よりも重厚、第5問がたまにゲロムズ…なイメージがありますが、今年はどうだったのでしょうか🤔❓
第1問

【解答】
(1) 易〜やや易
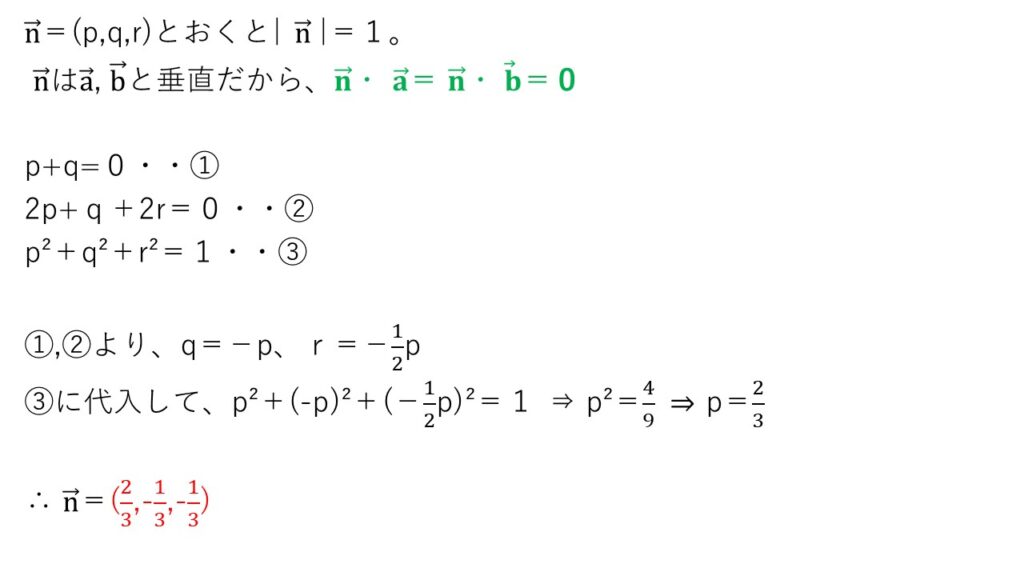
<分析>
ベクトルn→=(1,y,z)をまず設定し、内積=0から関係式を2つ出せばy,zが出ます。
あとはn→の大きさが1になるように縮小してあげれば、答は出ます☝️
(2) やや易〜標準

<分析>
Pから平面αに下ろした垂線の足をHとしてPH→を求めます。すると、OP’→=OP→+2PH→よりP’の座標が求められます。
(3) やや易〜標準

<分析>
これも、対称点に関する超典型的な問題ですね🤥☝️
(2)で対称点P’をわざわざ求めさせたのは何でだろ?と考えますと…PとQが平面αに関して同じ側にあると考えにくいからです。
<感想>
対称点を絡めたベクトルの問題。非常に典型的で、今回のセットではぜひ取りたいですね!
全統記述模試でも好んで出題されるタイプの問題なので、考え方まで含めてきちんと理解しておきましょう✊
第2問

【解答】
(1) 標準
<答1>

<答2>

<分析>
(答1)は河合塾の模範解答ですが、テクニカルで受験生的には難しい発想ではないかと思います。
むしろ、x^nを3次式(x-α)(x-β)²で割った余りをpx²+qx+rとおいて、(答2)のような変形をするとp,q,rを用いて表される実数A,B,Cが存在しますよ〜と示す方が受験生的には簡単でしょう🤥💡
(2) やや難

<分析>
B,Cは簡単。x=α,βを順次代入したら出ますので。問題はAですね。
x=α,β以外の値(0や1)を代入したところで、正体不明のQ(x)が邪魔してきます🤥
では、どうするか?ですが…
ここで、xnと(x-β)2の存在に着目し、微分したらどうかな?という発想を得たいところです(それが難しいんだけどね💦)
(3) 難

<分析>
(2)のAの正解が前提なのが辛いところです💦
本問では、βをαに近づけるので、平均値の定理f(β)−f(α)/β−α = f'(α)の利用を思いつきたいところですね。
とはいえ、βⁿ−αⁿ/β−α をシグマ(Σ)を用いた式に変換するのがまた難しい。
第3問

【解答】
(1) やや易

<分析>
「まず分数を整数と言い切るには何を言う必要があるか?」を考えましょう。具体的な数値を代入すれば話が早いですが、もちろんnが奇数であることが必要ですね☝️
では、どうやってnが奇数を言うか…ですが、それは、①の右辺がmに無関係に奇数であることに言及すればOKな訳です☝️
nが奇数をクリアすれば、与えられた2数の差が1であることに着目し、あとはお決まりの背理法(公約数をkとおく)でk=1を導けばOKです。
(2) 難


<分析>
(1)の結果を使うのだろうという推測は立つので、(n²-1)(n²+1)=2×3×5×7×m²はすぐ出ます。しかし、n²+1の方について3と7の剰余を用いた議論をする発想がかなり難しいですね😭
うーん、これは医学部でも捨て問扱いでいいでしょう。
(3) やや難

<分析>
(2)ができなくても、(2)の結果を使ってトライしてみることが大事です☝️
(84N+1)×8N=5m²より、左辺が偶数よりmが偶数であることがわかり、さらに(84N+1)×2N=5ℓ²まで出るでしょう。
「とりあえず1組求めればよい」ので、全部求めるような議論は必要ないのです。よって、Nが5の倍数の場合を考えるとわかりやすいでしょう☝️
ここで、2Lが平方数になるようなLを考えるとL=2がありますね。で、L=2のときたまたま420L+1=841=29の2乗となり解決。
<感想>
(1)は確保したいです。(3)は(2)の結果を使えば骨はあるけど解けます。しかし、(2)がむずすぎ…今年の最難問ですかね・・・私も手が出ませんでした🥲
第4問


【解答】
(1) やや易
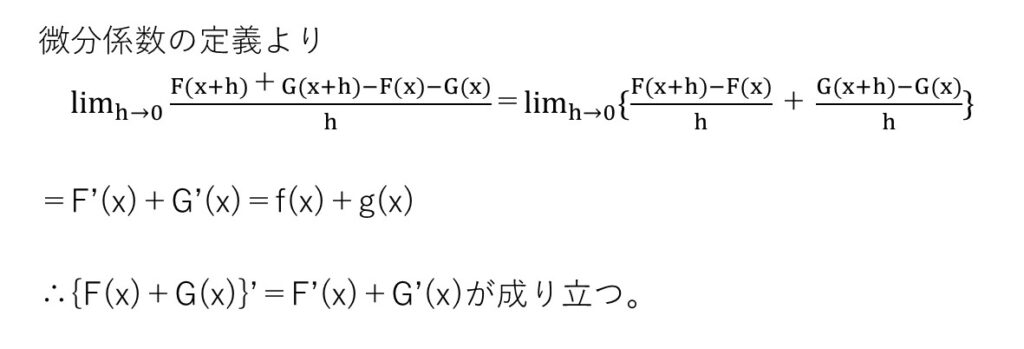
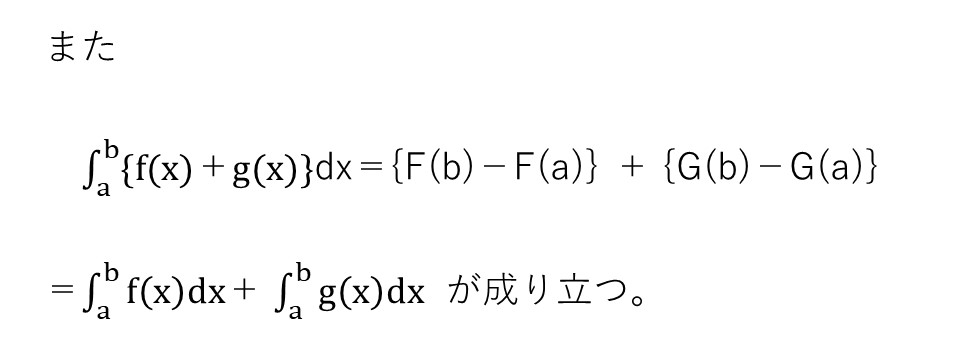
<分析>
「微分係数の定義をちゃんと覚えていましたか?」を聞く問題です。覚えていれば簡単です。
(2) やや易

<分析>
これも、平均値の定理を覚えてますか?という問題でした。覚えてさえいればやはり簡単でした。
(3) やや易〜標準
C
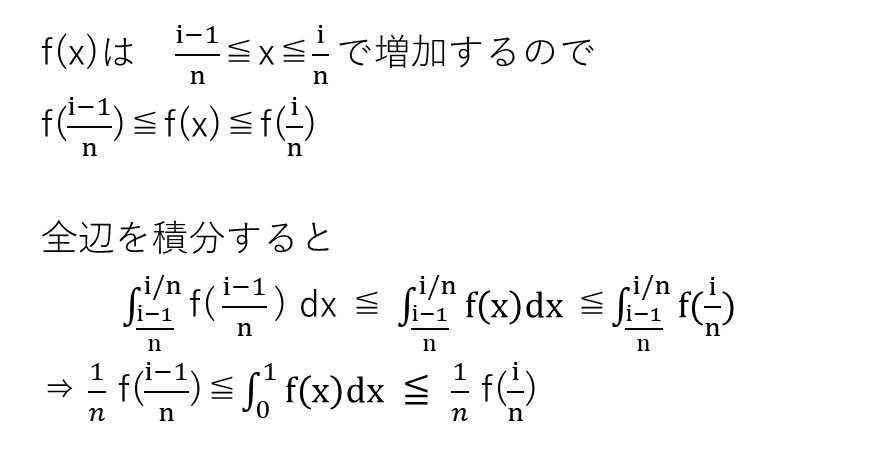
<分析>
今回はただ誘導に従えば解けますね。増加関数を扱うときに、上記の解法は東大模試なんかでも頻出のパターンです。もちろんノーヒントですが💦
(4) やや易〜標準
B

<分析>
(3)の式にシグマ(Σ)を付ければいいことはすぐにわかるでしょう。あとは、右辺のf(0)とf(1)をあぶり出すことでスムーズに解けます。
<感想>
問題の見た目はごついのですが、微分係数の定義と平均値の定理を覚えてさえいれば、実は拍子抜けするレベルで簡単でした🤣
第3問とは大違い(笑)
見た目に圧倒されて回避してしまった受験生は非常にもったいないですね〜。何事もチャレンジ精神って大事ですね✊
第5問

【解答】
(1) やや易〜標準

<分析>
まずは、素直に微分します。求めるのはdx/dtとdy/dxです。dy/dtではありません!
dx/dtはすぐに負がいえるので楽勝です。dy/dxの求め方は答を参照…この解法覚えておきましょうね💡
cost−cos5tはパッと見では正負の判断がつきませんが、ここで三角関数の和→積の公式を思い付けるとGood jobです☝️
(2) やや難
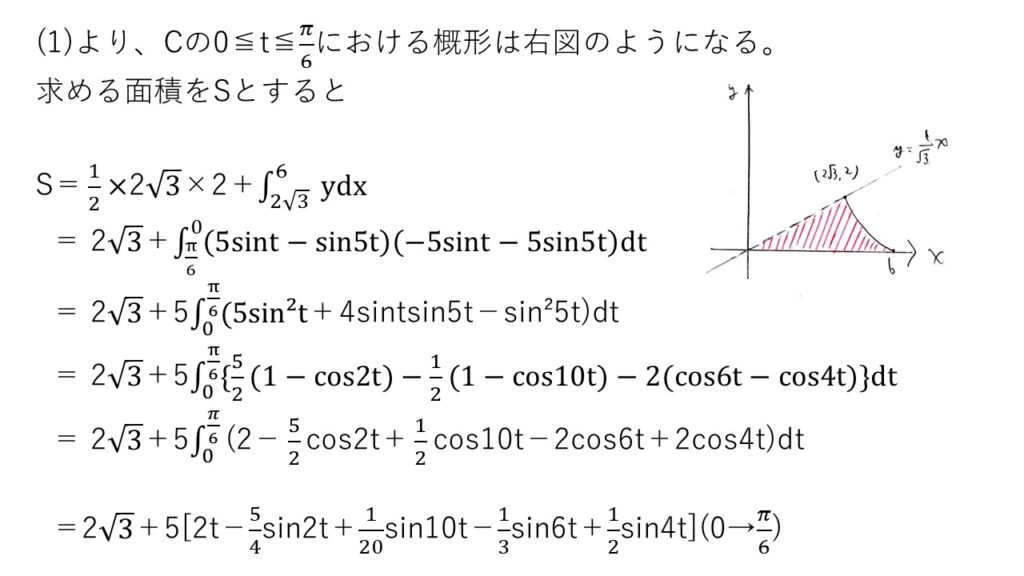
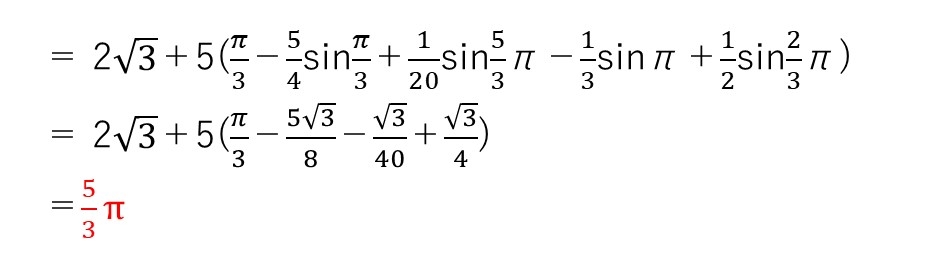
<分析>
面積の立式自体は難しくないですが、sintsin5tを三角関数の積→和の公式を用いて変換するのが本問の山場でしたね🤥💦
計算も結構面倒なので「やや難」レベルが妥当です。
(3) やや難


<分析>
x軸対称性は簡単です。後半は難しいですね。
解答では、「t+π/3を代入したものが結果としてπ/3回転した形になっている」という方針で示しましたが、-√3g(t)/2をig(t)×√3i/2と解釈する部分が結構難しかったと思います🤔
なお、tを代入したものをπ/3回転させてからt+π/3を代入した形にもっていくのは厳しいですね…方針によって明暗が分かれる問題でもありました💧
(4) やや易
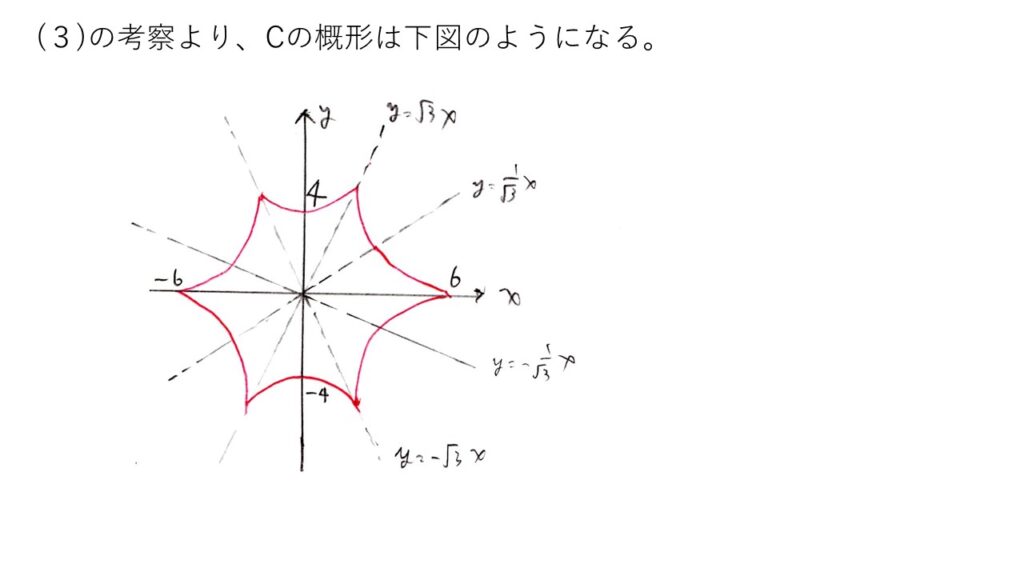
<分析>
(2)でt=0〜π/6の範囲の曲線が出ていればできます。(3)の2つの結果を使えば概形を書くのは難しくないです。むしろ(3)より難易度は低い😄
<感想>
(1)、(2)の立式まで、(3)の前半は簡単だったでしょう。sint sin5tの変形とできたかどうかで得点差がついたのでは?
(4)は実はサービス問題でした!最後がサービス問題ていうの、2021年の東大理系数学第4問でもありました😂😂
総括
去年よりかなり難化です。
完答のしやすさでいうと、1=4>5>>2>3ですかね🤔第2問は全体的に厳しく、第3問は(2)以降が難しく、第5問は計算と回転の部分が悩ましいというところ。
医学部志望者は第2問での崩壊を回避できたかが合否の分かれ目かと思います。
今回は難しいので、合格点は
非医:40〜45%
医:60〜65%
らへんでいいでしょう😅
最後に、再度公式LINEの紹介をします。
公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信する公式LINEはこちら👇
登録していただいた方には、無料プレゼント贈呈🎁の他、無料相談も受け付けております。






