受験生の皆さん、こんにちは。
東大合格ビジネスマンのワタシですm(__)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ 3大基礎力重視の裏ワザ勉強法
について、様々な情報を発信しております📢
今回は
公式LINE友だち追加を
してくれた高校生で
現在指導をさせていただいている
受講生の方から
実力テスト問題解説の
リクエストがありましたので
本記事で、わかりやすい解説を公開したいと思います🤔

(https://www.irasutoya.com/2020/06/blog-post_798.html?m=1より引用)
ちなみに、リクエストしてくれた高校生は地方公立トップ校に在籍しております。
なので、レベル的には
読者様の都道府県の公立トップ校並
と考えてください。
では、はじめに公式LINEの紹介をします。
公立中学出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってください✊
私も苦手科目は先生に頼りました。
また、LINE登録していただいた方には
無料プレゼント(1年で偏差値70出す画期的勉強法)
を贈呈します🎁
【⬇️公式LINE登録はこちら⬇️】

では、早速リクエストのあった問題2題を解説しましょう👍
一番のターゲットは
もちろんリクエストした高校生だ!!

(君だ イラスト – Bing imagesより引用)
解説するのは、数学ⅡBに属する
・円の方程式
・線形計画法
の2問です。
では、行ってみよー‼️
you tube版もあります👇
1:高2実力テストの問題
出題元は、某公立トップ校の実力テストの数学。
早速、問題を見るとします。
【第1問】

<リクエスト内容>
(1)がわからず(2)(3)も雪崩失点してしまった。
模範解答を見ても、なぜC₂の中心が(△ , □)なのかわかりません。
ちなみに、同じクラスの学年トップ層(5位以内)の人は完答できたようです。
<私の解いた感想>
ふむふむ、(1)はポイントが2つあるなー。
数学弱者は1つめで躓くけど、数学得意でも割り切りが苦手なタイプは2つめで詰むだろうなー。
フィーリング(勘)で運良く正解する受験生もいるだろうけど、ゴマカシなしの詳しい記述を求められると減点対象だろうな。
しかし、(2)もなかなかの曲者だな…
計算ごり押しで凌げなくもないけど、なるべく煩雑な処理を回避してスマートに解くにも、意外とめんどくさい!
【第2問】

<リクエスト内容>
(3)の解法が皆目見当が付かなかった。
模範解答を見て色々考えたけど、全く腑に落ちない。
<私の解いた感想>
(1)(2)は超基本的で、共通テストでも易しいレベル。それに比べて、(3)の難度ときたら…
飛躍的に難しくなってないか??
直接2点間の距離を評価しようとすると詰むし、ワンクッション挟むにしても、その発想は東大・京大受験生でも悩むレベル。
見たことある解法と言えば見たことある解法なんだけど、今回はいつもと違って「そこで使うんかい!?」って感じ。
2:超詳しい解答・解説
では、先ほどの2問の超詳しい解説をしていきます。
その前に1つ注意喚起すると、一度自分で頭を捻ってから解説を見てください‼️
では、いきます。
【第1問】
(1)
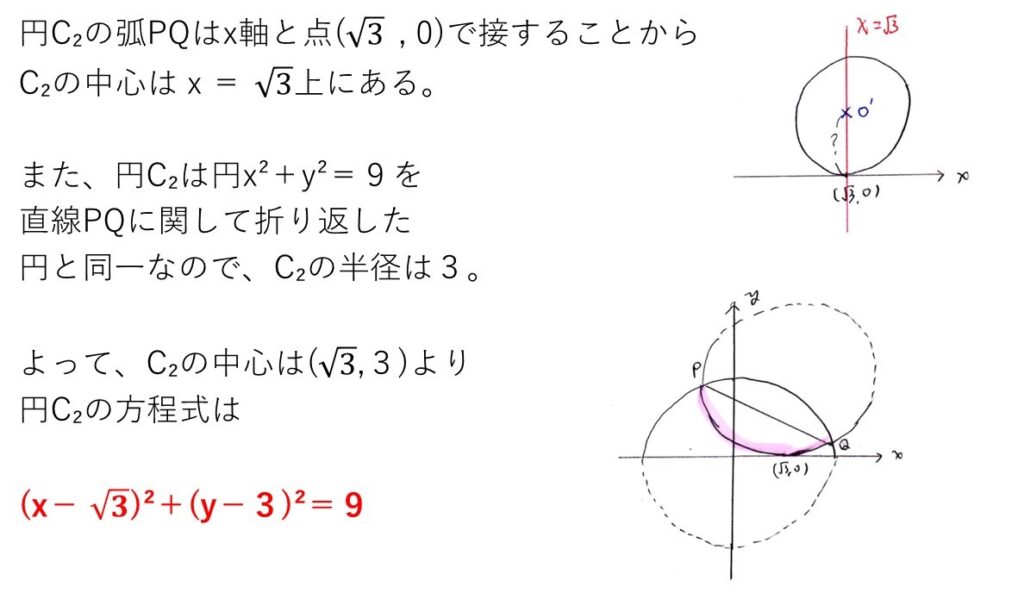
以上が解答ですが、ここのポイントは以下の2つですね。
① x軸は円C₂の接線
② 円C₂の半径は3①は中3レベルですが、折り返した後の弧PQに意識を奪われると見逃す箇所だと思います。x軸が接線だとわかれば、C₂の中心は接点(√3,0)を通るx軸に垂直な直線上、つまりx=√3上にあることがわかります。
さて、問題の②です。これは勘で答えは出せますし、今回その勘は見事に当たるでしょう。
しかし、この手の問題は、数学に得意意識があるけど納得しないと先に進めないタイプの受験生が諦める嫌〜な問題です。「とりあえず(1)の答を出せば(2)(3)は解けそうだな」と思ったら、えいやと勘で押し切る度胸も受験には必要ですね💦
とりあえず勘で答える場合。
背理法的考察で挑めば、何となく半径が3だろうな〜という推測はつくでしょう🤔
例えば、円C2の中心が点(√3,5)にある場合を考えてみましょう。
すると、弦PQの長さは変わらず半径は変わるので、円の中心角と弧PQのくびれが変わります。
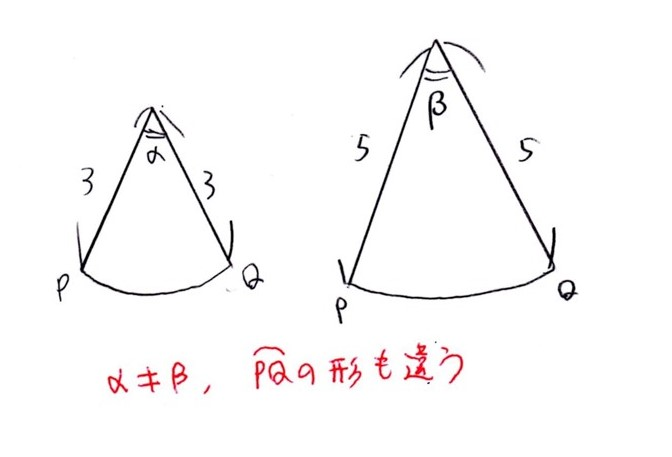
このイメージはわきますか??
円C2の弧PQはが円x2+y2=9の弧PQと形状は全く同じである点からも、なおさら半径3でないと都合が悪そうだなと思えませんか?
(2)

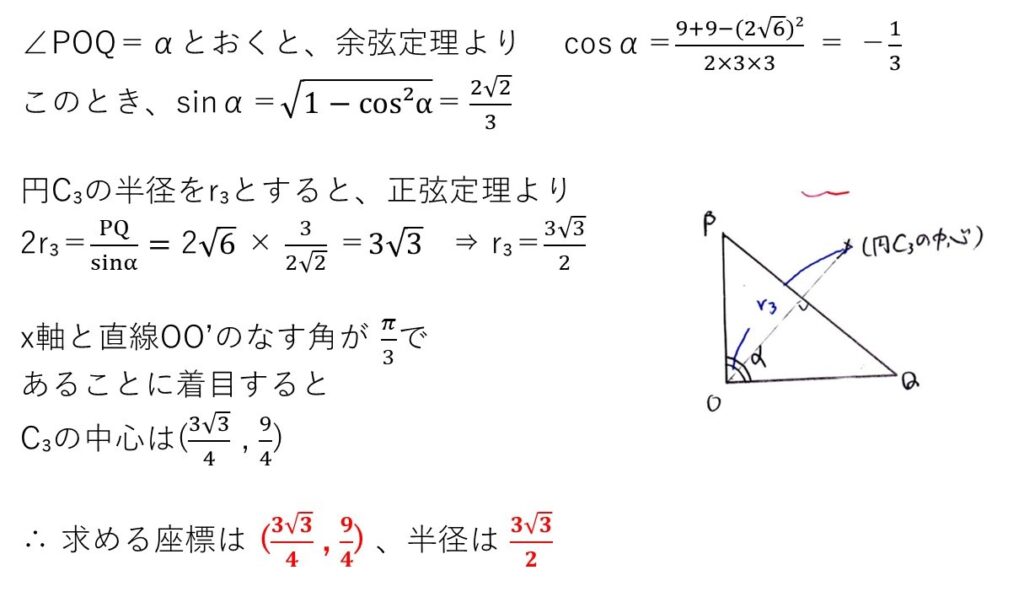
△OPQがOP=OQの二等辺三角形であり、円C3が3点O,P,Qを通ることから、円C3の中心はOとPQの中点(M)を通る直線上にあるといえます。
次に、OM=√3 と三平方の定理からPQ=2√6を出して△OPQに余弦定理・正弦定理を順次使うことで、Oと円C3の中心との距離がわかり、C3の座標が求まるわけです。
依頼者に学校の模範解答を見せてもらったのですが、やはり係数k,ℓを用いたこのような機械的な解答が為されていました👇

これでも解けるのですが、大半の受験生は意味わかって使っているのでしょうか?
特に説明もなく「〜を考えると」だと、意味もわからず公式丸暗記に走る受験生が多発してしまうと思うのですが…
学校の先生が作りそうな答案だよな〜、とは思うけど🥱
(3)

(2)ができればオマケ問題です。
C3の中心をO”とすると、O’A+O’O”+O”O=一定より、ABの長さが最大になる状況は解答の図の状況であると理解できるでしょう。
【第2問】
(1)
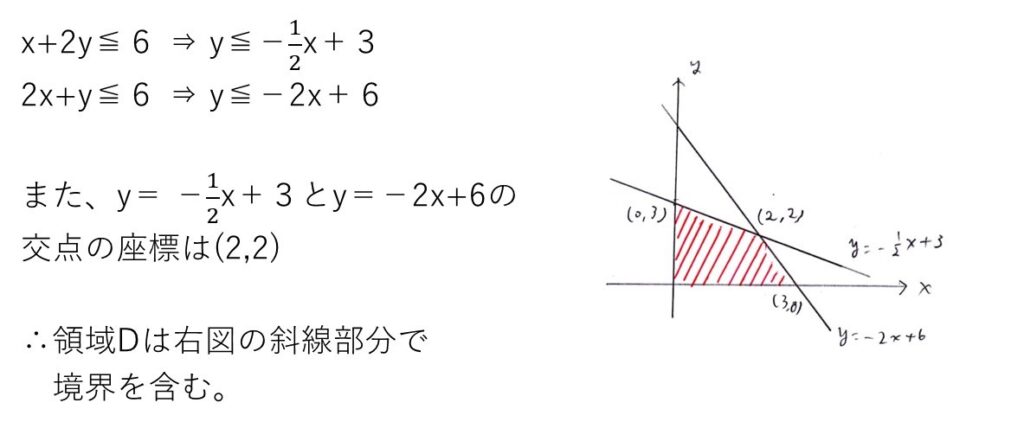
超基本。y≦−2x+6の意味はわかりますよね?y=−2x+6より下側の領域(境界含む)を表します。
(2)

円の中心(a,6-a)の軌跡をxy座標で表したい場合は、(a,6-a)=(x,y)としてaを消去するのが鉄則でした。
aは実数全体を動くのでxの定義域も実数全体となりますが、xy絡みの式に変換する際は必ずx(y)の動く範囲を意識しましょう!
ここまでは簡単なんだ、ここまでは。
次が問題の(3)。
依頼者によると、学年で完答者は1人だけだったようですよ。
では、解答を示しましょう👇
(3)
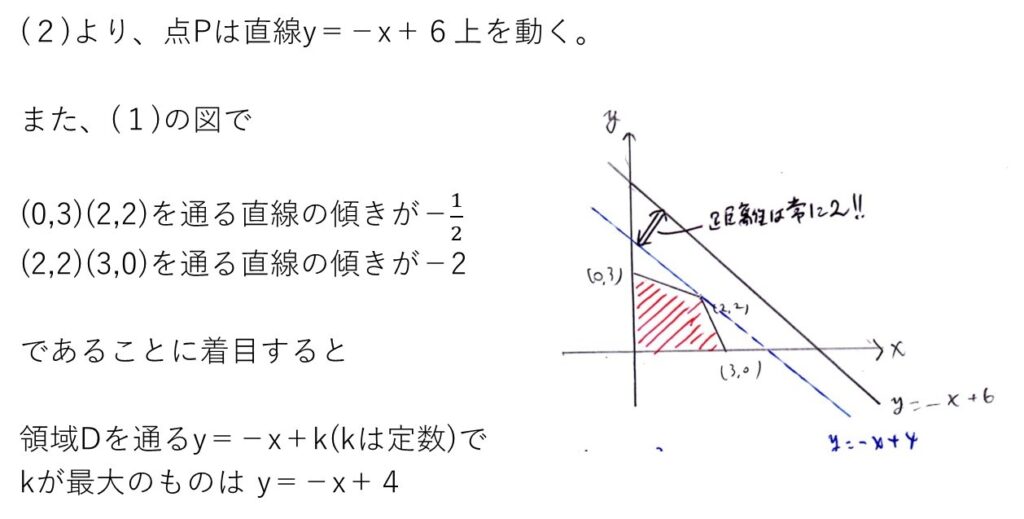
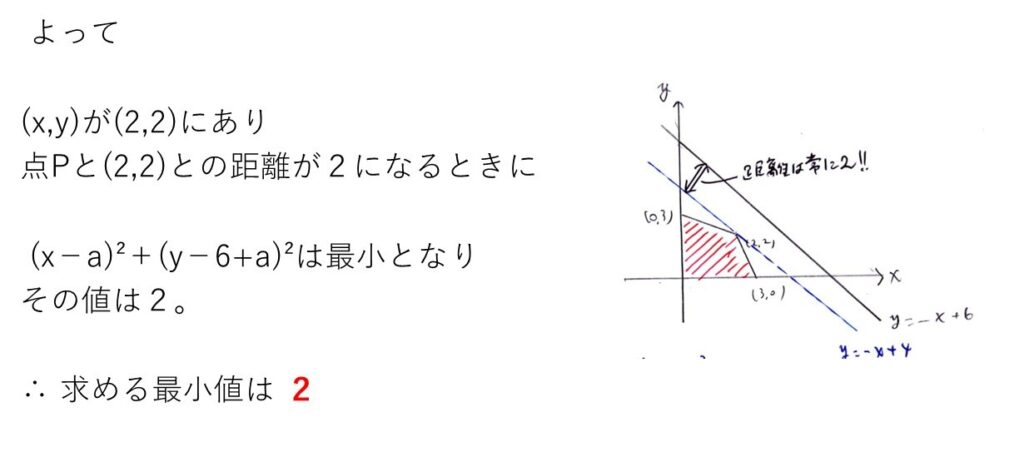
ふぅ、大変だった。
でも、一応答えは出たから一件落着かな…
と思ったあなた‼️
この解答、間違いなんですよね💔
何が間違いか?
もう一度問題文を読んでみましょう👇

aを定数
「aを定数」って書いてます!!
依頼者も国語が苦手なのですが、同じく国語弱者の私も同じ間違いをやらかしておりました💔

(https://stampo.fun/tag/なんだと/より引用)
つまり、y=−x+6 , x=a , 領域Dの形より
aの値によって最小値は変わるよ!
ということです。
実際の模範解答がこちら👇
場合分けが5通りも生じておりますねー。

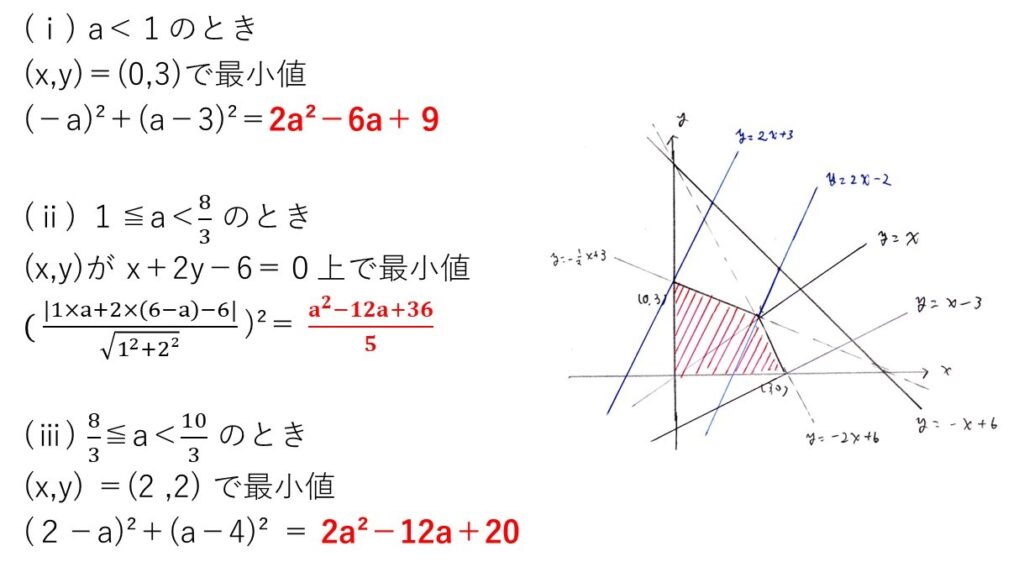
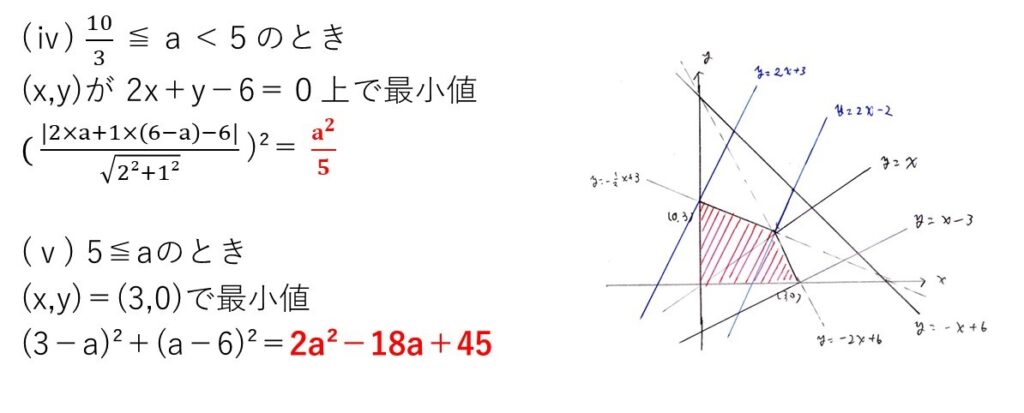
これは東大模試ならよくある考え方ですが、公立トップ校の高2レベルでは非常に難度が高い問題です。
xを次第に増加させて、(x,6-x)と一番近そうな直線がどれか当たりをつけ、さらに点と直線の距離の公式を用いて最小値を求める。
また、場合分けの境界は「ある点を通るある直線に垂直な直線」を考えることで決める必要がありました。
こういう思考ステップを踏む必要がありました。
しかし、大変だ〜😅
(4)
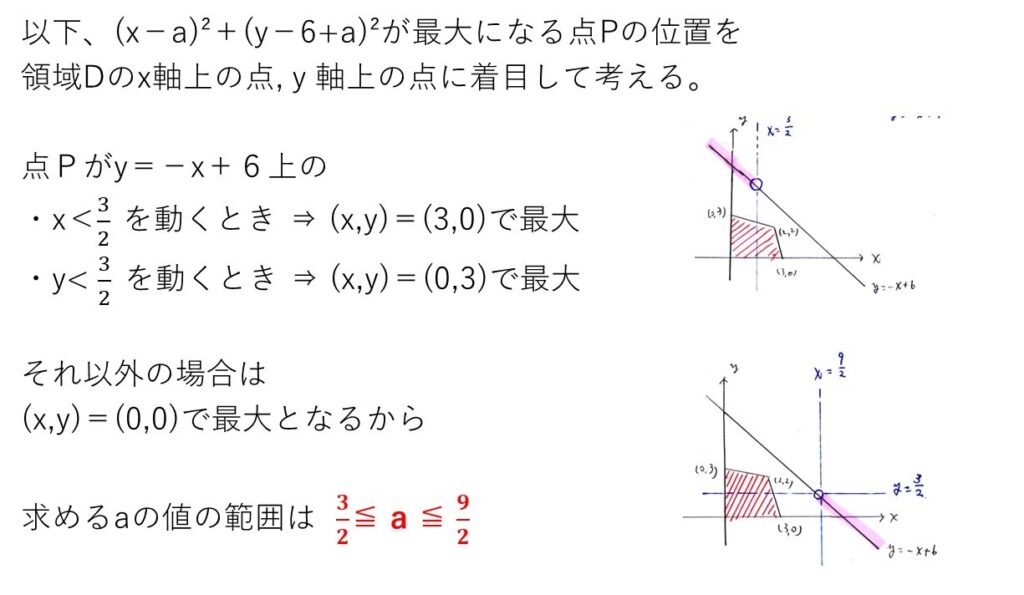
今度は最大値です。(4)の方が(3)より易しいのに、何で(4)を後にした❓
問題の意図は
一番遠い点が(0,0)になるPはどこ?
でしたね。
これも
xを増加させる(=yを減少させる)と
D周囲のどの線上で一番遠くなりそうか?
を実験してイメージする作業が大事であると言えます。
例えば、xが小さい(yが大きい)ときはどうか?というと…
x軸上の(3,0)が一番遠そうだけど、点Pを次第に右下に移動させるにつれて一番遠い点が(3,0)から(0,0)にチェンジする瞬間が訪れそうですね。このとき、Pのx座標は3/2。
その後しばらくは(0,0)が一番遠い状況が続きますが、yが0付近に近づくとが一番遠い点が(0,0)から(0,3)にチェンジする瞬間が訪れそうです。このとき、Pのy座標は3/2。
以上よりaの範囲は解答のようになります。
では、以上でリクエストに挙がった数学Ⅱの問題2題の解説を終わります。
今回の問題解説が、視聴者の受験生の皆様の数学力アップに繋がらんことを願っております🙏
では、最後に、再度公式ラインの紹介をします。
私の公式LINEでは、無料相談を随時受け付けております。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってみてください✊
【⬇️公式LINE登録はこちら⬇️】