
受験生の皆さん、こんにちは。
東大合格ビジネスマンのワタシですm(_ _)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ 3大基礎力重視の裏ワザ勉強法
について、様々な情報を発信しております📢
私の公式LINEでは、無料相談を随時受け付けております。
公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってください✊
私も苦手科目は先生に頼りました。
また、LINE登録していただいた方には
無料プレゼント(1年で偏差値70出す画期的勉強法)
を贈呈します🎁
【⬇️公式LINE登録はこちら⬇️】

you tube版がこちら👇
問題
【第1問】




【第2問】




【第3問】




解答解説
【第1問】
(ア)(イ) 易
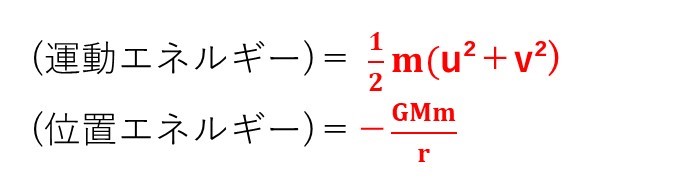
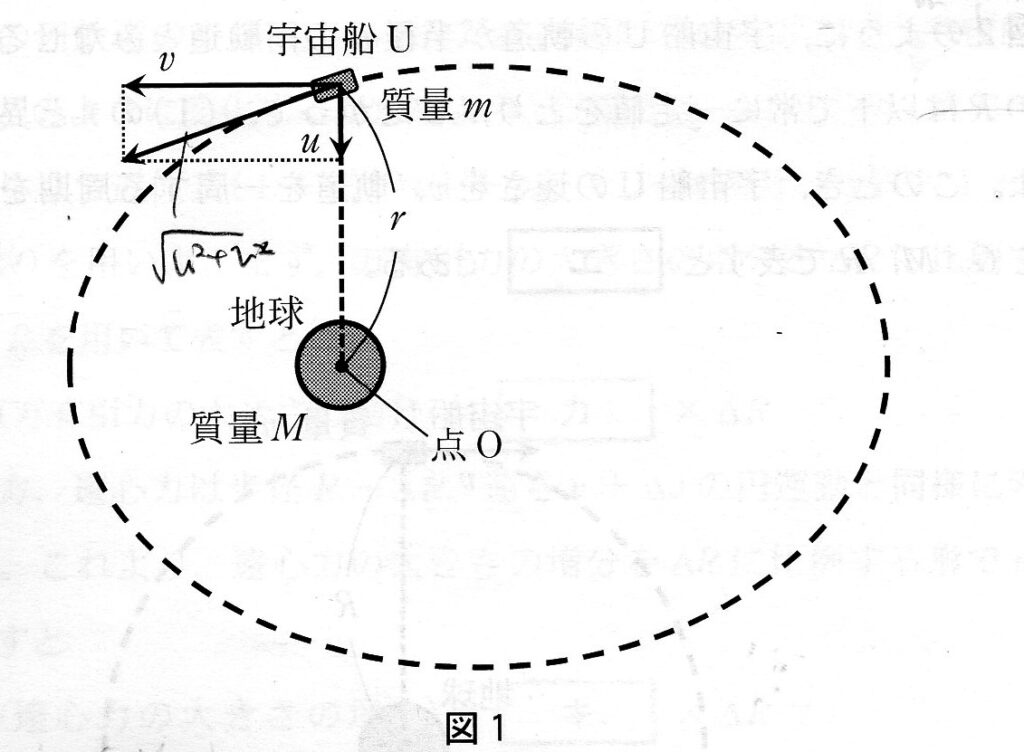
宇宙船Uの速さは√u²+v²なので、運動エネルギーは上式で表されます。
また、位置エネルギーの基準は無限遠で0なので、宇宙船Uが地球に近づくごとに位置エネルギーは減少します。
(ウ) 易〜やや易

vではなくSを用いて表すので、vをSで表してvを消去することを考えましょう。
(問1) 標準

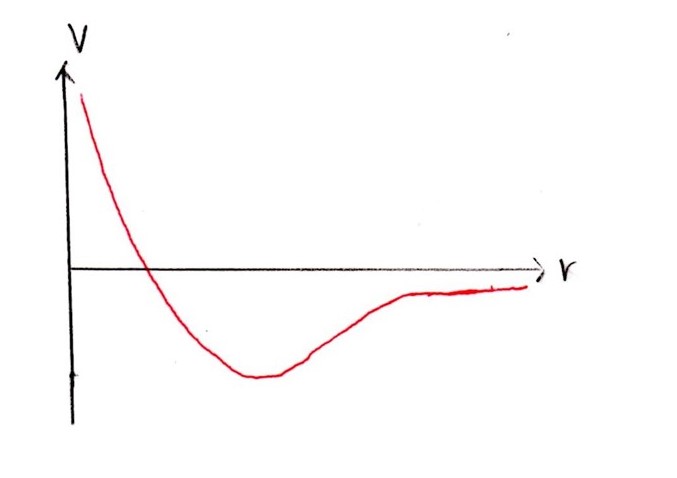
地味に数Ⅲ極限の問題。
r→∞でV(r)→0は自明ですが、r→0のときはどうするか?
V(r)はr²で括ると( )の中身は定数となるので、極限は+∞に発散します。
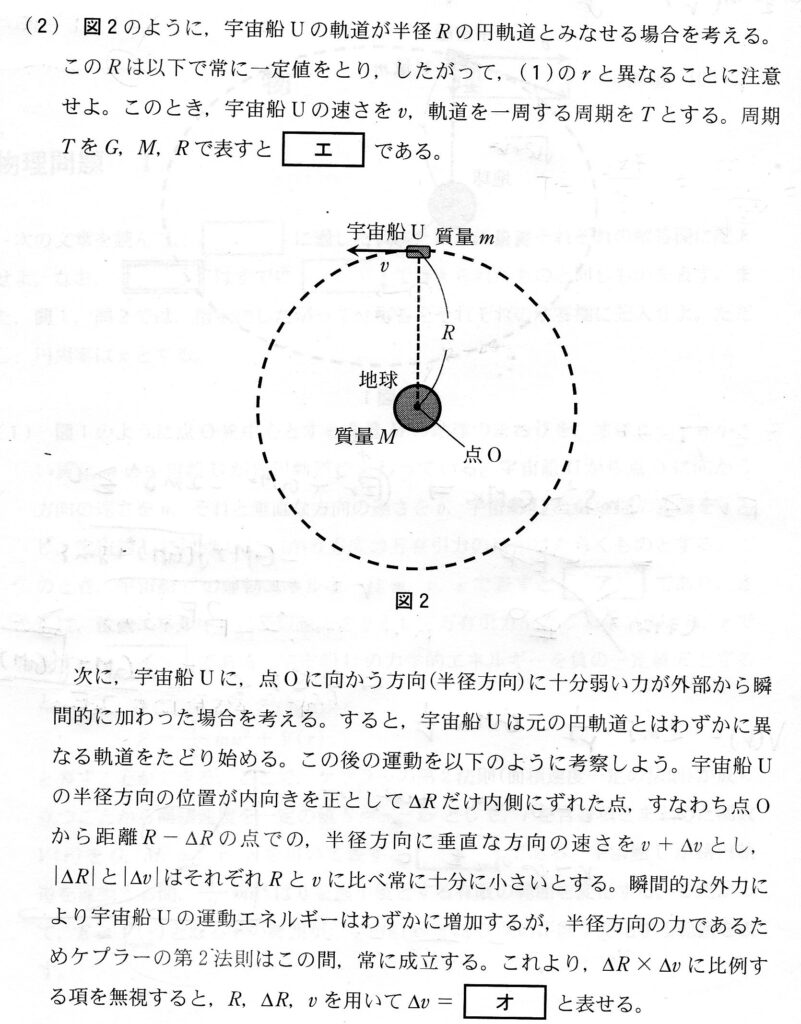
(エ) 易〜やや易
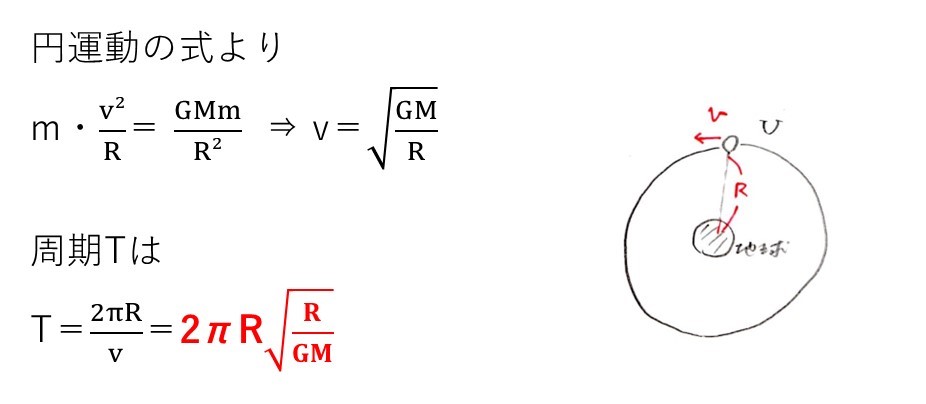
等半径の等速円運動をするので、(速さ)×(周期)=(円周の長さ)から求めればOK。
(オ) 易〜やや易

本問は誘導に従い、微小量の積=0を用いることでΔvが導出できます。
(カ) やや易

問題文の指示に従って、近似式を用いて処理です。
(キ) 標準
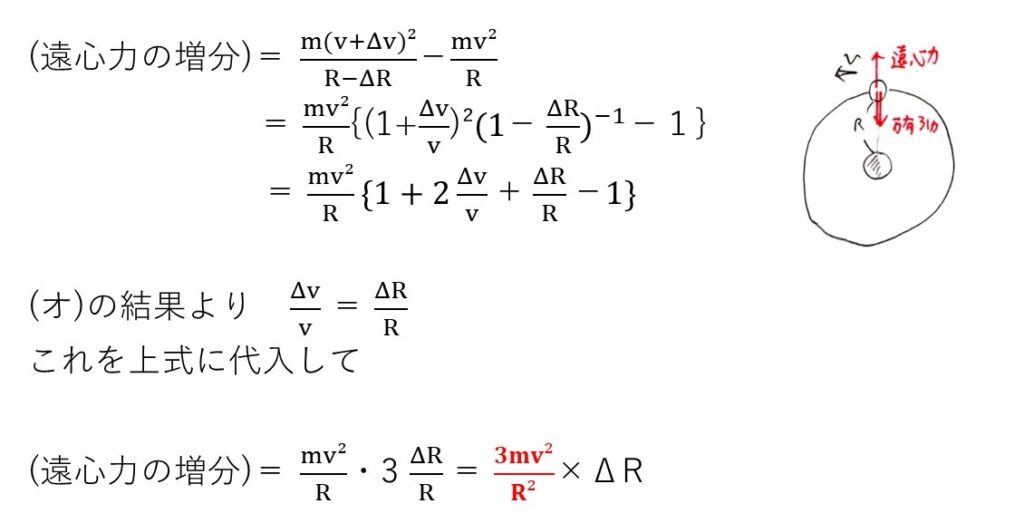
問題文の指示に従って、近似式を用いて処理です。
(ク) 標準

(カ)(キ)の正解が前提ですが、解答にvは使えないので、vにGM/Rを代入することを考えましょう。
(ケ) 標準

(ク)で求めた合力の増分がΔRの比例式となり、しかも係数が負なので、宇宙船Uは単振動をします。
よって、角振動数ωが求まり、(周期t)=2π/ωよりtが求まります。
(コ) やや易
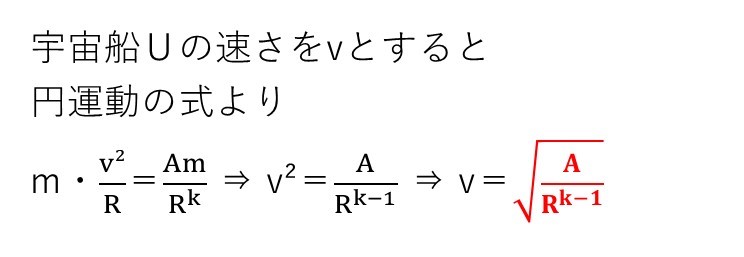
やることは(エ)と同じで、右辺は万有引力がAm/R^kに変わっただけです。
(サ) やや易

やることは(カ)と同じです。
(シ) 標準
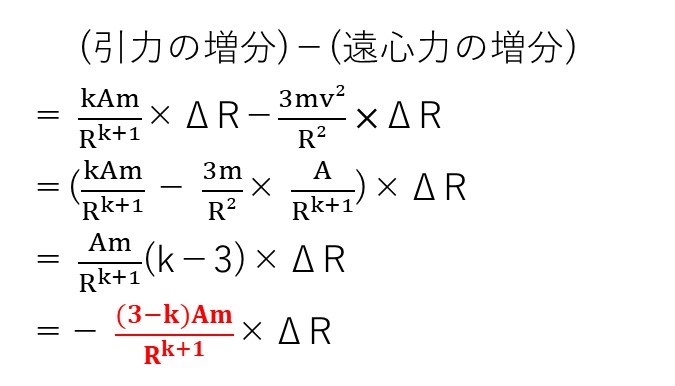
やることは(キ)と同じですが、ここでもvを消去することを考えます。
(ス) 標準

ΔRの係数が負となるようなkを定めればOKです。
(セ) 標準
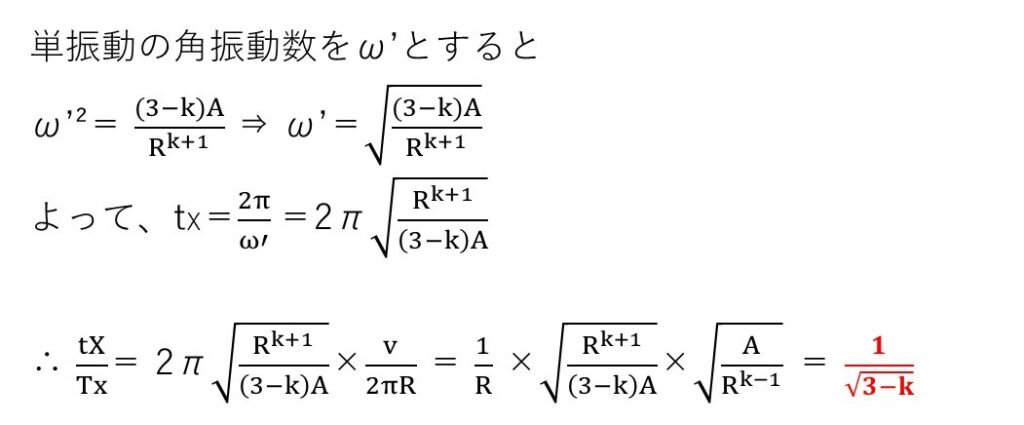
やることは(ケ)と同じです。
(問2) 標準

k>3では合力の増分は正となり、ΔR=0では不安定なつり合い式が成立します。
ΔR<0では宇宙船Uは天体Xから遠ざかり、ΔR>0では天体Xに近づきます。
【第2問】
(イ) 易

4πkQを丸暗記していた受験生もいたでしょうけど、本問は問題文に定義の説明があり、それをもとに立式すれば難なくできます。
(ロ)(ハ)(ニ) 易〜やや易
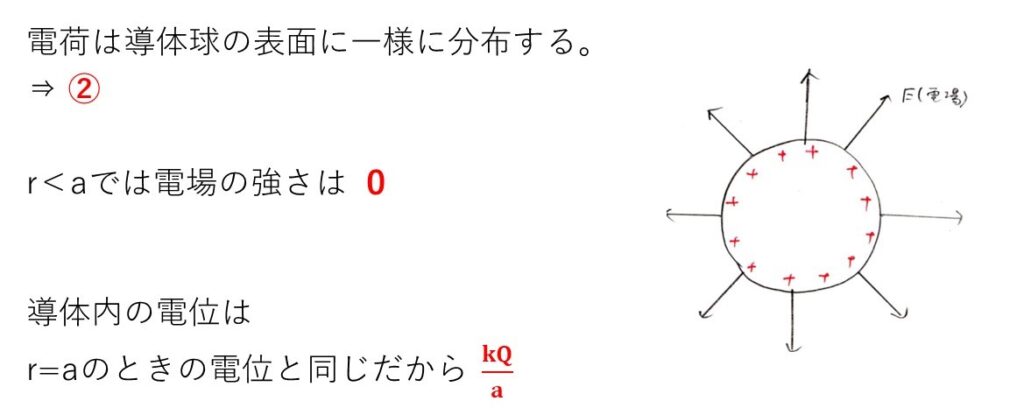
導体の性質を把握しておけば、本問も難なく処理できます。
電荷は表面に分布し、その結果導体内部の電場は0(=電位は一定)になります。
(ホ) やや易
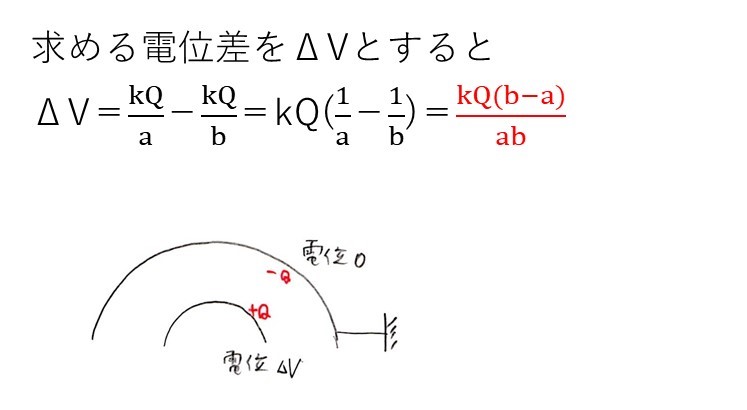
アースは余計でした、忘れてください😓
求める電位差ΔVは正なので、電位の大きい方(r=aのとき)から小さい方(r=bのとき)を引けばOKです。
(問1) 標準〜やや難
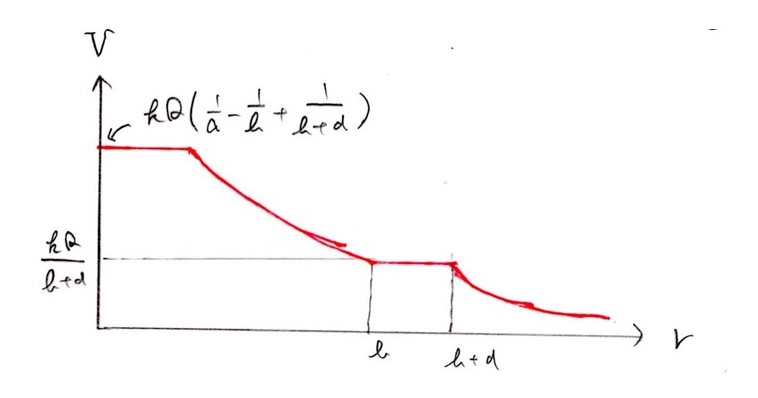
電位の基準は無限遠で、導体の電位が一定であることを意識できれば、上図を描くのは難しくありません。
kQ/b+dを出すのは公式通りで難しくありません。ではr=0での電位はどうなるかというと、kQ/b+dに(ホ)で求めたΔVを加えればよいのです。
(へ)(ト)(チ) 標準

解答はC=の誤りですm(_ _)m
アース(接地)するとはどういうことか、理解できていますか?
Bの電位は地球と同じ0となり、B外側の+Qは地球(アース)に移動します。B内側の−Qは移動しません。なぜなら、A外表面の+Qが静電引力で−Qを引きつけて離さないからです💡
また、a≦r≦bの状況はアースの前後で変わらないので、AとBの電位差はΔVのまま。あとは電気容量をCとしてCΔV=Qを用いてCについて解けば完了です。
(リ) やや難

ノーヒントで電場の式を思いつくのはやや難しいですが、解答にQを使えないことをヒントにQ=V₀/Cを用いることを考えたいところでした。
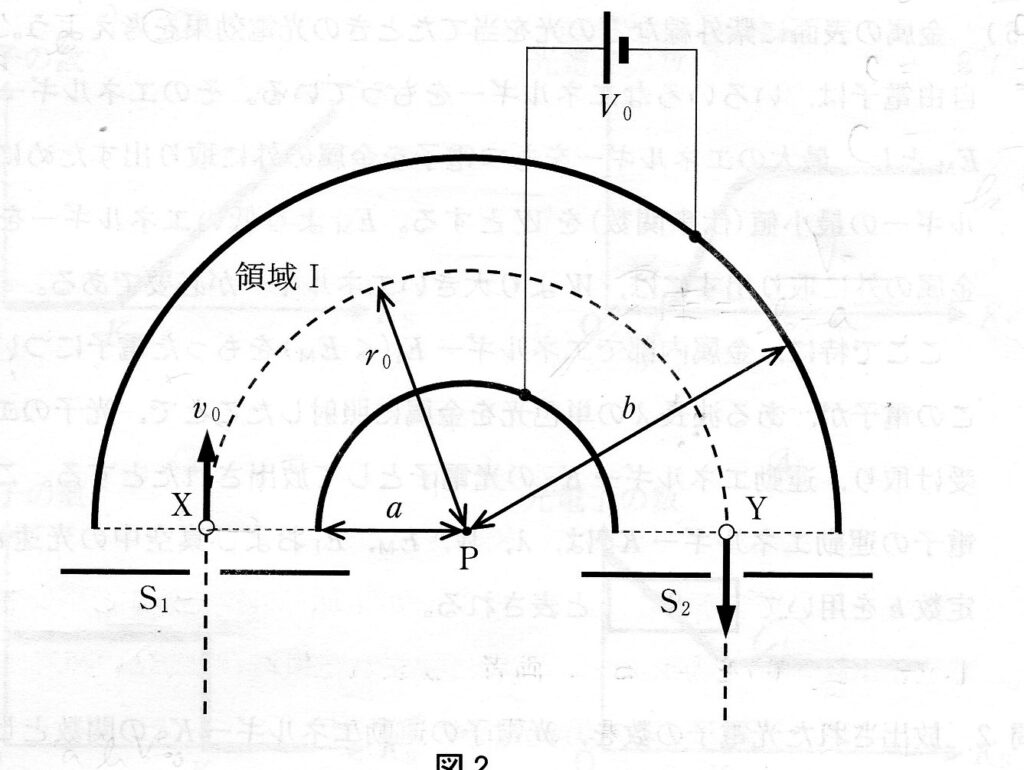
(ヌ) やや難

運動エネルギーを求めるには速さが必要。では、その速さは何で求めるのかというと、何でしょうか?
本問では「等速円運動」がテーマになっているので、電場から受ける力を向心力とする円運動の式から求めればよいと気付きたいところです。
(ル) やや難
本問の解答には光電効果の理解も必要ですが、問題の意味を汲み取るのに苦労する受験生が多いと思います。
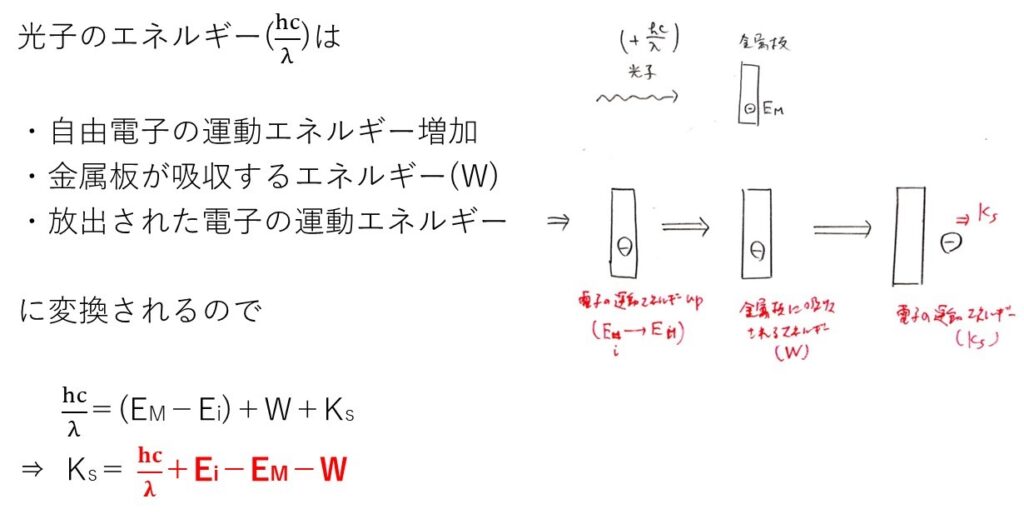
問題文の流れをよく読むと「光子が金属板に衝突→金属板にエネルギーの一部が吸収され、電子がエネルギーKsで飛び出す」と解釈できます。
つまり、光子のエネルギーは
自由電子にエネルギー(EM−Ei)を与え
金属板にエネルギーWを与え
残りで電子をKcで飛び出させたと考えると超わかりやすいと思います🫠
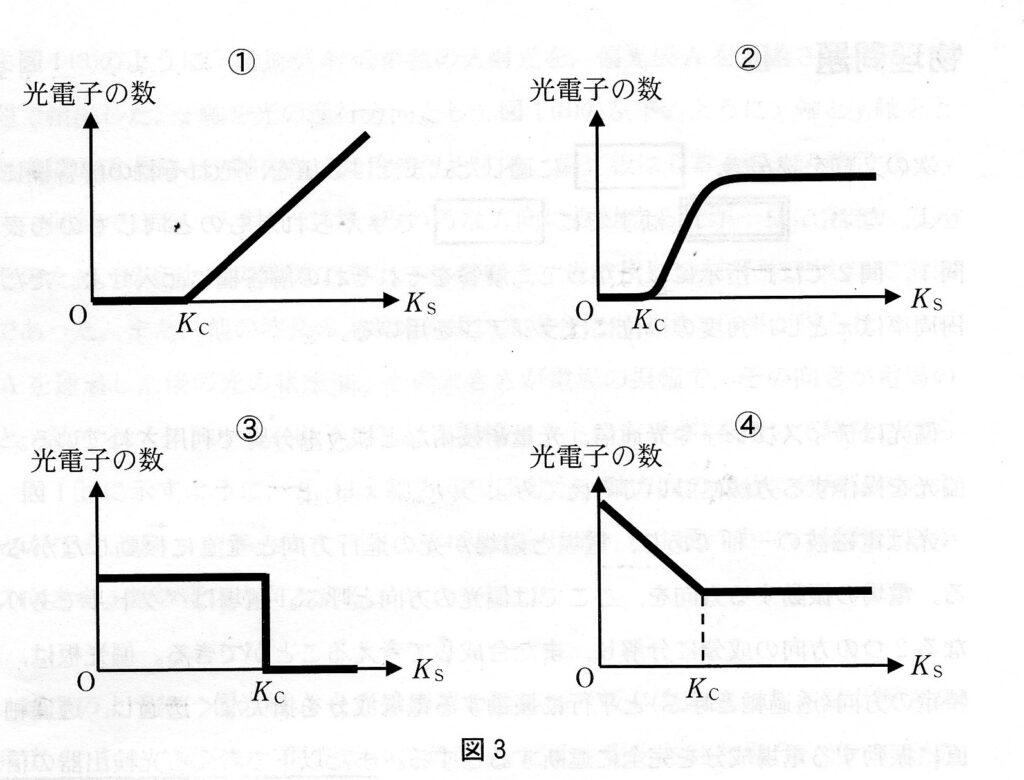
(問2) やや難
③

ここでは光子のエネルギーhc/λを一定として考えるため、Kc以上の運動エネルギーをもつ電子は存在しません。
しかも、金属板中には「さまざまな運動エネルギーの電子」が存在することから、各々のエネルギーをもつ電子数も変わりません。
【第3問】
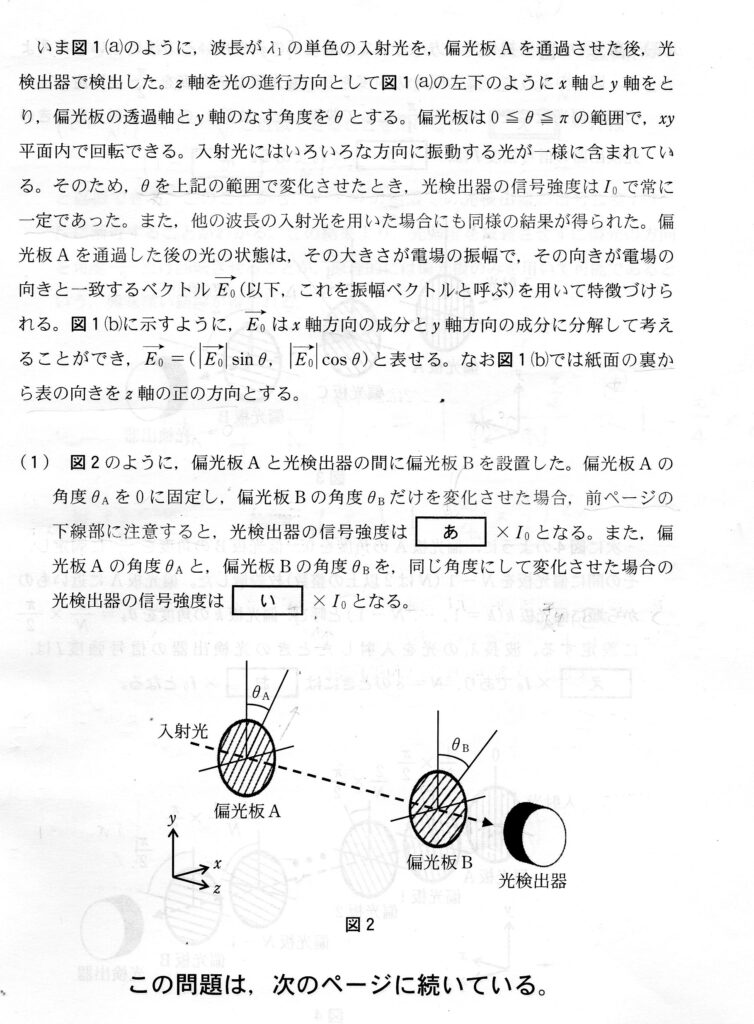
(あ) (い) 標準
2023年の京大受験生が面食らった、偏向板の問題。
本問は題意を理解すれば何ともない問題なのですが…厄介なことに その題意を正しく理解するハードルが高いのですよ😵💫
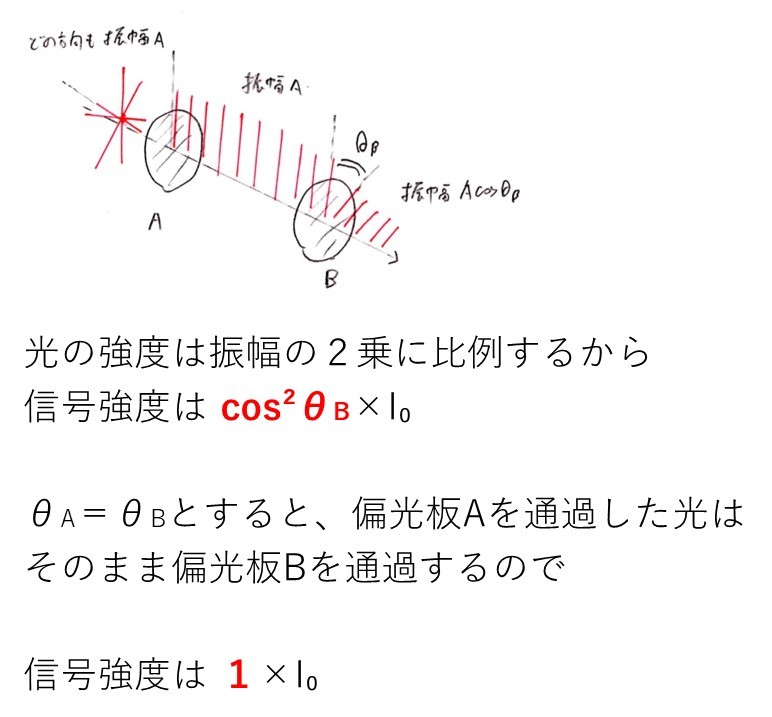
本問では
偏向板Aはθ=0向きの波以外の波は全てカットし、今度は偏向板Bを通るとその振幅はcosθ倍になると解釈してほしい
のです。
しかし、それだけでは間違えます。
「下線部に注意すると」を見逃さないように注意しましょう☝️
求めるのは強度で振幅の2乗に比例する点を考え、(cosθ)²を答えることになります。
(う) 標準
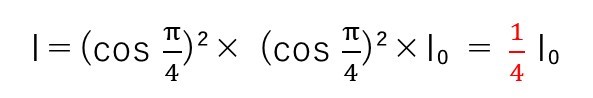
(1)で偏向面の特徴を把握できれば、(あ) (い)の応用。(cosπ/4)²× (cosπ/4)²より、答は1/2。
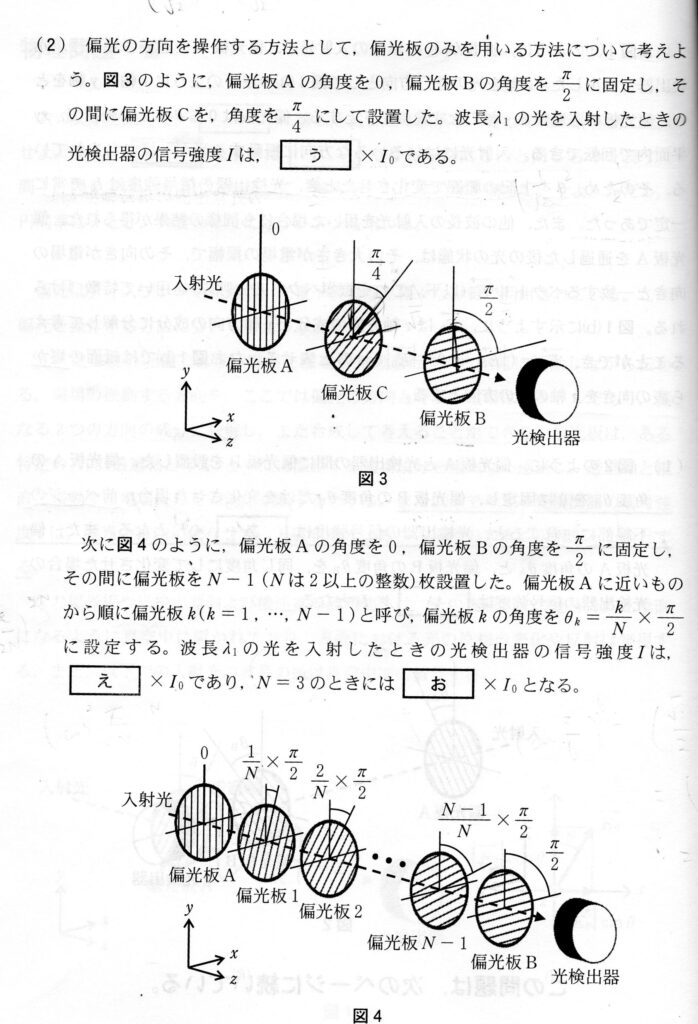
(え)(お) 標準〜やや難

角度がπ/2Nずつずれる現象がN回ずつ起こるので、強度は(cos π/2N)^2N 倍となります。(お)は(え)の答にN=3を代入するだけ。
(か) やや難
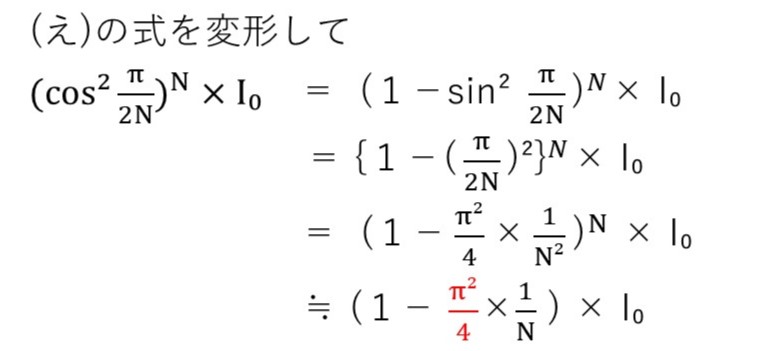
(え)の正解が前提ですが、aに当たるものを炙り出し問題文にある近似式を用いればOK。
(き)〜(さ) やや易

本問は題意がよくわからなくても、誘導に従っていつもの「光路差=波長の半整数倍」を用いれば一気に解決できるサービス問題。
(問1) やや難
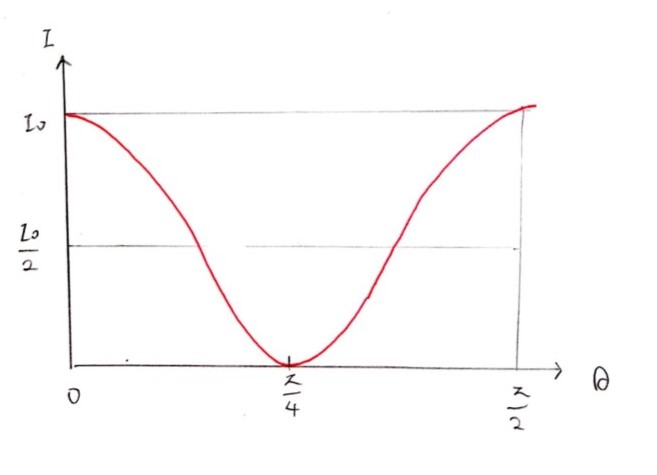
d=d₀のときθ=π/4が3π/4に変化することをヒントに、一般の鋭角θ(0≦θ≦π/2)で角がπ−2θずれることを導出すれば本問は解答可能です。
π/2 ≦θ≦πのときは、対称性を考えれば調べる必要は省けます。
(し) 標準

本問は実は隠れたサービス問題でした。光路差λ₁/2を20倍すると10λ₁になり、今度は「強め合う条件」に相当するので、信号強度は最大値I0をとります。
(問2) やや難〜難

ここまでの流れが把握できたか否かで、体感難易度が変わる問題です。
本問では、10λ₁の距離がλ₂の半整数倍だと考え、m=10のときにΔλが最小となることを見抜けば解答可能です。
繰り返しになりますが、私の公式LINEでは無料相談を随時受け付けております。
また、LINE登録していただいた方には、無料プレゼント(1年で偏差値70出す画期的勉強法)を贈呈します🎁




