
受験生の皆さん、こんにちは。
東大合格ビジネスマンのワタシですm(_ _)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ 3大基礎力重視の裏ワザ勉強法
について、様々な情報を発信しております。
私の公式LINEでは、無料相談を随時受け付けております。
公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってください✊
私も苦手科目は先生に頼りました。
また、LINE登録していただいた方には
無料プレゼント(1年で偏差値70出す画期的勉強法)
を贈呈します🎁
【⬇️公式LINE登録はこちら⬇️】

2021年入試、旧帝大の第5弾は
「大阪大学」です。
当ブログの解説記事は
読者が必死に3年間努力すれば
東大(理三以外)・京大(医以外)・九大医
レベルに80%以上の確率で合格できる
ことを目的に作成しています✊
市販の問題集のように、解法を丁寧に示すだけではありません!
多角的なアプローチで問題を解きほぐしています✊
① 各問の難易度
② 他分野や一般常識との関連事項
③ 問題の躓きポイント
④ 極力曖昧な表現をしない説明
を示しています。
イマイチ成績が突き抜けられない受験生に貴重な情報が提供できればと思いますm(__)m
阪大理系数学の特徴
大阪大学の理系数学は全5問で、制限時間は150分です。受験生レベルを考えるとやや重いですが、全6問の東大に比べると時間的余裕は多少あります😲
今年の阪大は阪大らしく重いセットでした💦
ただ、約10年前と比べると最高難度はマシなので、数学強者は8~9割の得点も可能なセットでした。
今年の難易度だと、深く理解するには
全統記述模試で偏差値63~68程度
は欲しいですね🧐
第1問

【解答】
(1) やや易
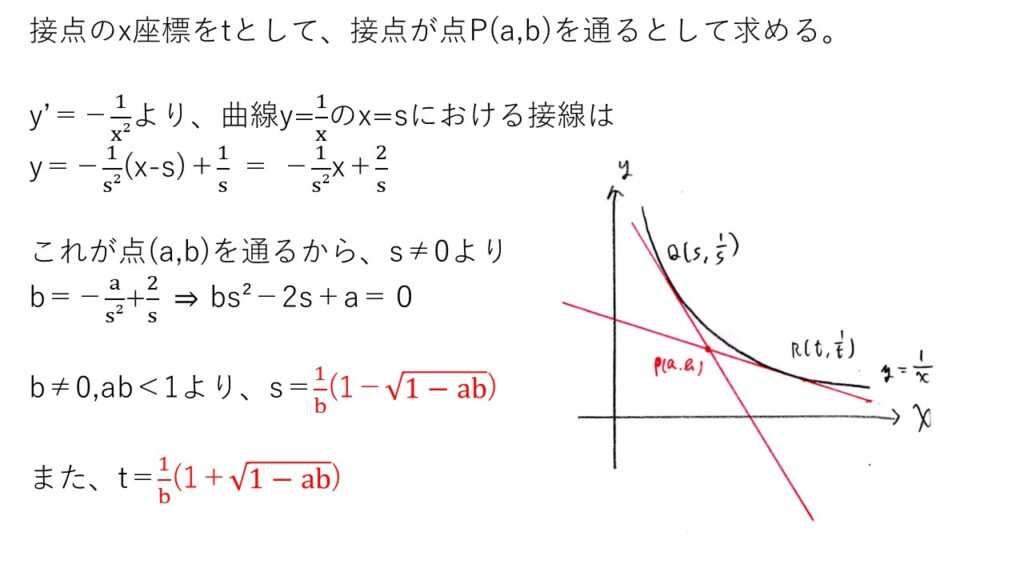
<分析>
曲線の接線が絡む問題では、接点のx座標をsなどとおく手法が有効であることが非常に多いですね💡
本問も接線をsを用いて表し、それが点(a,b)を通るという条件からsの2次方程式に持ち込みました☝
(2) 標準~やや難


<分析>
まずaの変域を求め、t/sをa,bで表すのが先決でしょう。
ここで、分母,分子にabの塊があること、abがaだけで表されることに着目すると・・・ab=kとし、kの範囲も限定してしまうとスムーズに進みそうだなと考えられます🤔
<感想>
よくある、微分して接線の問題のようですね。捻りは若干あるという程度で、完答はしやすいと思います。
ただ、(1)の解法で明暗が分かれたかもしれません😓接点のx座標をtとおくと簡単に済みますが、点(a,b)を通る直線を定めて判別式に持ち込むと計算がエグイことになるので、見極めが必要な問題でした。
第2問

【解答】
(1) やや易~標準



<分析>
「同一平面上にある条件」「一次独立の性質」に着目する問題でした👀
まあ定番といえば定番。全統記述模試でも頻繁に出てくる問題なので、旧帝大を目指す受験生ならきちんと押さえておきたい問題ですね💡
<一次独立について>
下図参照👇
ここでは、「独立」と「従属」の違いがわかればOKです。a₃がa₁,a₂で作られる平面上にないときは、s,tをいかなる値にしてもa₃=sa₁+ta₂で表せないですよね💦💦
仮に(1)のA₀Qの式でOCの係数が0でないとすると、OCがOA,OBを含む式で表されてしまうことになりますが、これは不適切ですよね。なので、各係数=0でなければならないのです☝
(2) やや易~標準

<分析>
これはオマケ問題。(1)ができれば即答でしょう😂
<感想>
同一平面上のベクトルを実数s,tと2つのベクトルを用いて表す手法は頻出問題だと思いますが、今回のセットでは一番ふつうな問題でしたね🙄
第3問

【解答】
(1) 易~やや易


<分析>
旧帝大志望者なら絶対に経験がある問題です。辺々引き算して微分、単調性を示すという超典型問題。
(2) やや易

<分析>
中辺の形を見た時点で、反射的にt~t+1/nの範囲で積分だな💡とわかるでしょう。
そして、直観通りに積分計算をしていくと、与えられた不等式の形が出てきました👏
(3) やや難
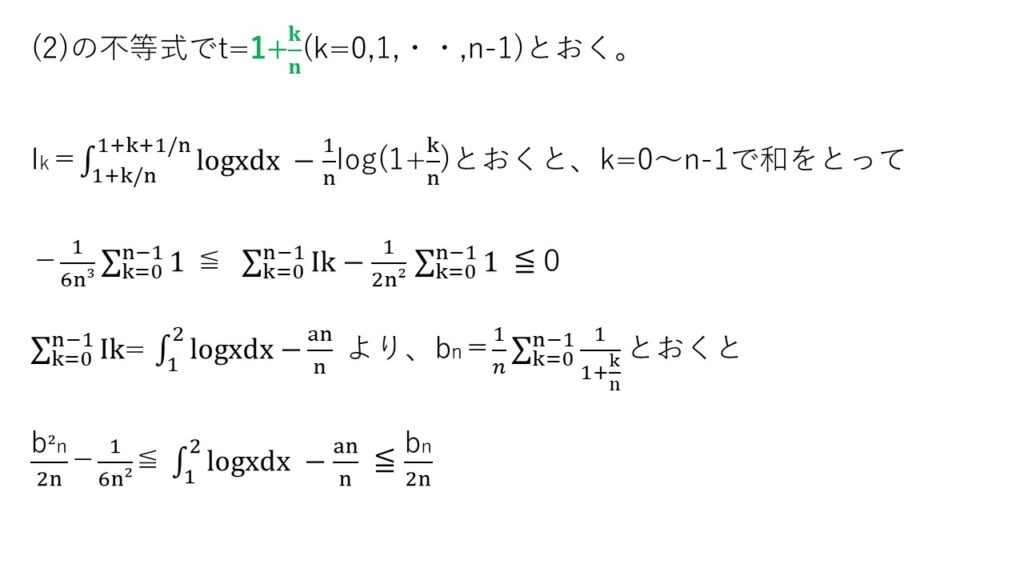
ここで、bn=∫dx/1+x (x:0 → 1)=log2。

<分析>
(2)までは仏の顔で対応してくれたけど、(3)では鬼の対応してきましたね👹
tに何を代入したらいいかがわかりにくいのが難点ですね~😭anにシグマ(Σ)が含まれることから、k/nを出す発想はしたいところでしたが・・・それでも難しい💦
<感想>
(1)は超頻出タイプで実際に簡単ですが、(2)(3)に進むにつれて骨のある問題と変化していきます。
(1)
差をとって微分の非常によくある典型問題なので、できないとヤバイです。
(2)
左辺と中辺は(1)の不等式の左辺と中辺をxで積分すると出そうだ!と見当をつけたいですね☝
(3)
tに何を代入するかで明暗が分かれますが、それをクリアしてもなかなか煩雑💦
第4問

【解答】
(1) 標準~やや難

<別解>



<分析>
(別解)の方は処理が多少メンドクサイけど「2a+b,a+2bの一方が3の倍数となることはない」・・(*)を考えるよりは発想面では簡単かな~と思いました。
(*)を思いつかずに詰んでしまった受験生も結構いたのではないでしょうか😭😭
(2) やや難

<分析>
3c²=-(2a+b)(a+2b)の形を出すこと自体は難しくないので、(1)の証明ができなくても解けます。その点は救いでしたね💦
あとは、解答のように整数k,ℓを用意して候補を絞ればOKでした。
<感想>
整数問題です。
(1)(2)とも難問ではないけど、受験生の弱点(盲点?)を突いてくる問題だったと思います。
「(2a+b)と(a+2b)の和が3の倍数であることから2a+bとa+2bがともに3の倍数」をいう部分が盲点だったかなと思います💦解法に詰まった方はよく復習しておきましょう。
第5問

【解答】
(1) やや易
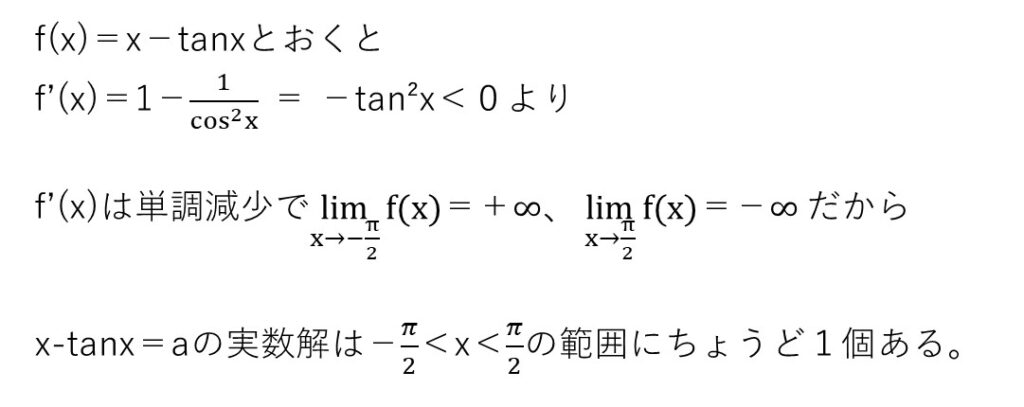
<分析>
これは感覚的に明らかでしょうけどね・・・y=xとy=tanxのグラフを描いて、「図より自明」なんか書いたら当然×です😵
ちゃんと数式で示しましょう。
(2) 標準


<分析>
x=tにおける接線がy=sinxと接する条件を直接調べにいくと何も見えてこないので、
x=t’における接線と一致するという観点からアプローチしたい問題でした💡
そうすると、現に(1)の事実も使えますからね😳
<感想>
三角関数絡みの問題ですか・・・(1)は当たり前だろ?と思うのはよ~くわかりますが、式証明しないと点がきませんので、面倒だけどきちんと示しましょう✊
(2)はなんかややこしそうですが、手を動かすうちに解法が見えるのかもしれませんね🧐
総括
今回のセットでは、完答難易度の低い第1,2問は押さえたいところです✊
第3~5問は1,2問より手強いですが
完答難易度でいうと3>>4>5
の印象でしょうか。
第3問は(2)までは取りたいですが、(3)はtに何を代入するかの判断が難しいしその後の処理も手強いので、落としても仕方ないでしょう。
第4問はキー問題でした🔑
(1)の証明は闇雲に進めるとできなくなるし、(2)も整数に慣れていないと詰まった可能性が高いでしょう。
第5問は最終問にしては、割と簡単めでした。(1)は面倒くさがらずに取るとして、(2)は「ある接線が別の接線とも一致する」という方向性で示すとよかったでしょう。
合格点は
非医:50~55%
医:70~75%
程度でしょうか🤔
最後に、再度公式ラインの紹介をします。
私の公式LINEでは、無料相談を随時受け付けております。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってみてください✊
【⬇️公式LINE登録はこちら⬇️】





