
2022年大学入試、旧帝大の第2弾は「東北大学」です。通称「とんぺー」
当ブログの解説記事は、読者の成績を最難関レベルまでグングン伸ばすことを目標にしており、
読者が必死に3年間努力すれば東大(理三以外)・京大(医以外)・九大医レベルに80%以上の確率で合格できることを目的に作成しています。
市販の問題集のように、解法を丁寧に示すだけではありません!多角的なアプローチで問題を解きほぐしています
① 各問の難易度
② 他分野や一般常識との関連事項
③ 問題の躓きポイント
④ 極力曖昧な表現をしない説明
を示しています。
イマイチ成績が突き抜けられない受験生に貴重な情報が提供できればと思いますm(__)m
私の公式LINEでは、無料相談を随時受け付けております。
公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってください
私も苦手科目は先生に頼りました。
また、LINE登録していただいた方には
無料プレゼント(1年で偏差値70出す画期的勉強法)
を贈呈します
【


東北大物理の特徴
東北大の理科は2科目で150分。そのうち、物理は分量も多めで導出過程も書くため、案外時間を奪われます。
一方の化学は割と軽め。よって、75分目標にしたいけど、80~85分までならかけてOKな感じです
2000年代前半の重くて難解な物理からすれば、だいぶ弱体化したなあという印象は拭えません。
受験生的には有難いのでしょうけど
第1問


【解答】
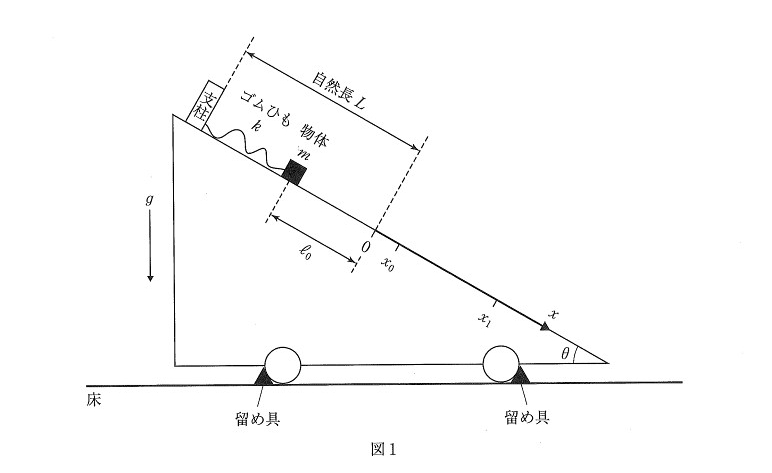
(問1)
(a) 易

<分析>
斜面方向の力のつりあい式を立式すれば、すぐに出ます!
(b) 易〜やや易

<分析>
ゴムひもが縮んでいるときは弾性エネルギーは考えなくてOK。よって、(重力の位置エネルギー)=(運動エネルギー)より求めればいいですね
(c) 易

<分析>
指示通りにUを求めればいいだけです。簡単。
(d) 標準
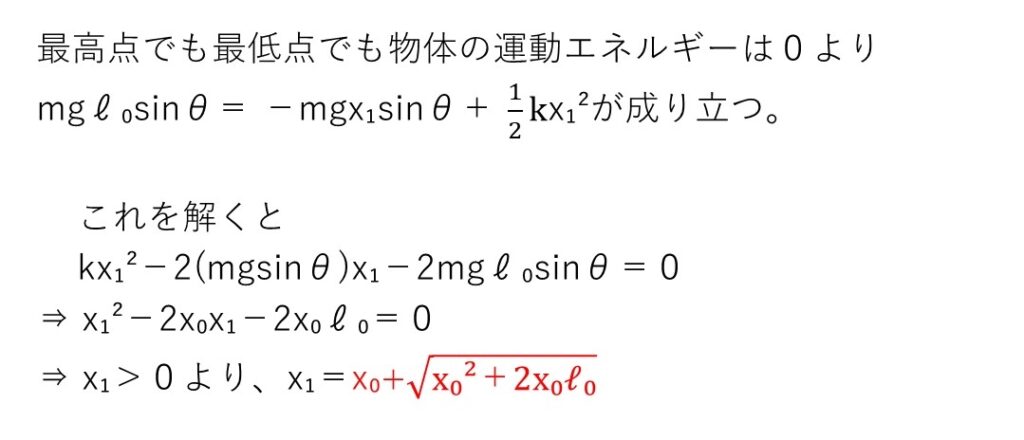
<分析>
最高点でも最下点でも運動エネルギーが0であることを考えると、mgℓ₀sinθがUになったと考えて解けばOKです
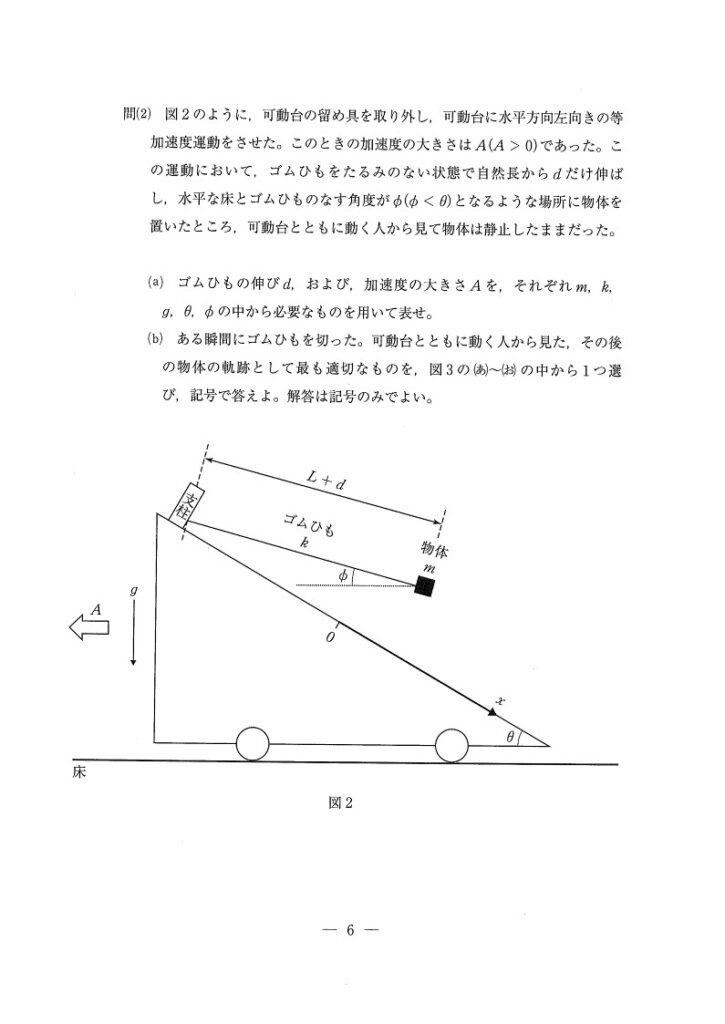
(問2)
(a) やや易

<分析>
求めるものはd,Aの2つ。可動台からみて静止するので、慣性力を考え、鉛直方向と水平方向でつり合いの式を立式すればOKです。
(b) やや易〜標準
う
<分析>
可動台の人から見るので、慣性力は残ります。すると、水平方向にも鉛直方向にも加速度運動をするということになり、軌跡は直線です!(う)方向に見かけの重力√A2+g2を受けて等加速度直線運動をするとみなせます
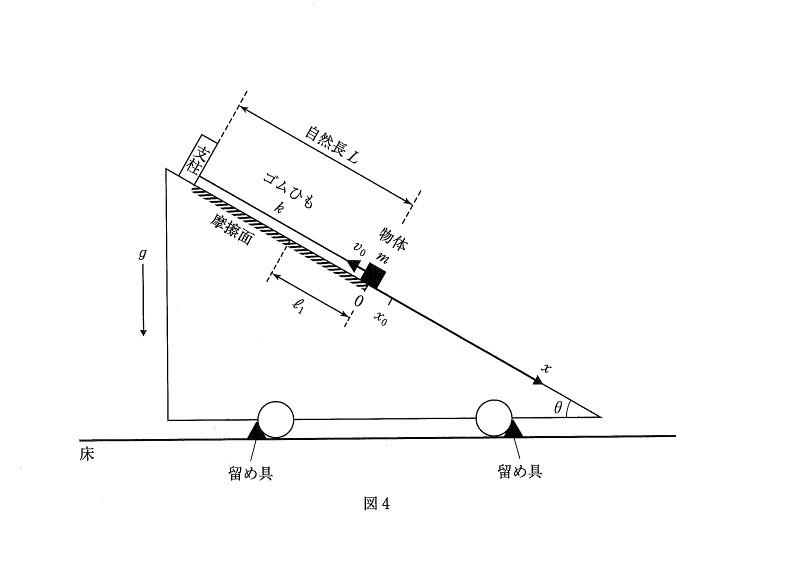
(問3)
(a) 易

<分析>
重力と動摩擦力を用いてx軸方向の運動方程式を立てるだけです。
(b) 易〜やや易

<分析>
加速度aを使うことから、斜方投射で頻出の公式の利用を考えます
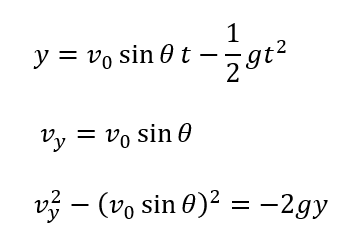
(c) やや易〜標準

<分析>
斜面を下るときも加速度を求めて(b)と同じ処理をすればOKです
また、動摩擦力が距離2ℓ₁分だけ仕事をすると考えてエネルギー収支の式を立式しても解けます。
(d) 標準

<分析>
vnを求めたいので、vnとvn-1の関係式を出したいところです。
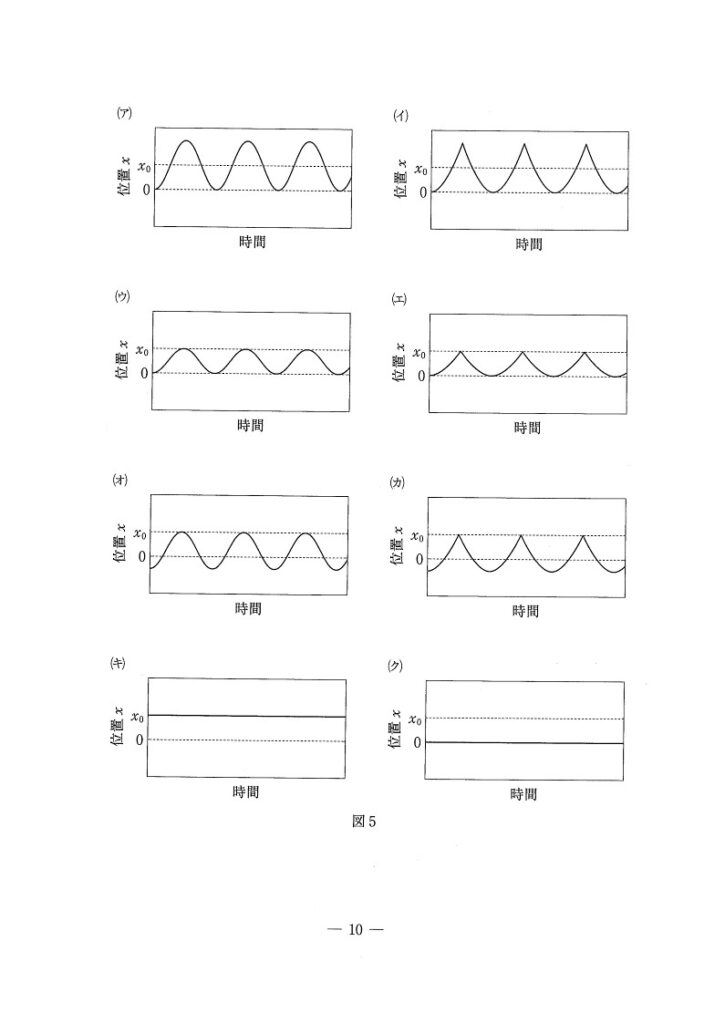
(e) 標準〜やや難
ア
<理由>
公費v₁/v₀は1より小さいので、N→∞のときx=0を通過するときの物体の速さは0に近付く。よって、中心をx₀、振幅をx₀とする単振動になる。
<分析>
N→∞とするとx=0での速さがほぼ0であり、さらに、つりあいの位置がx₀であることに着目します。最終的に、物体はx=x₀を中心とする振幅x₀の単振動をします
<感想>
めっちゃ普通の運動方程式,慣性力,エネルギー収支の問題。物理が得意な受験生なら完答も全然いけます!!
幾何的な難しさもなければ、着眼の難しさもない・・・以前の東北大物理はいずこへ
第2問

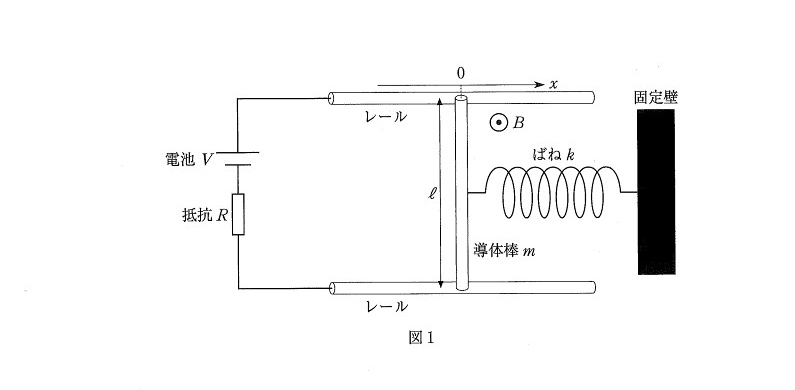

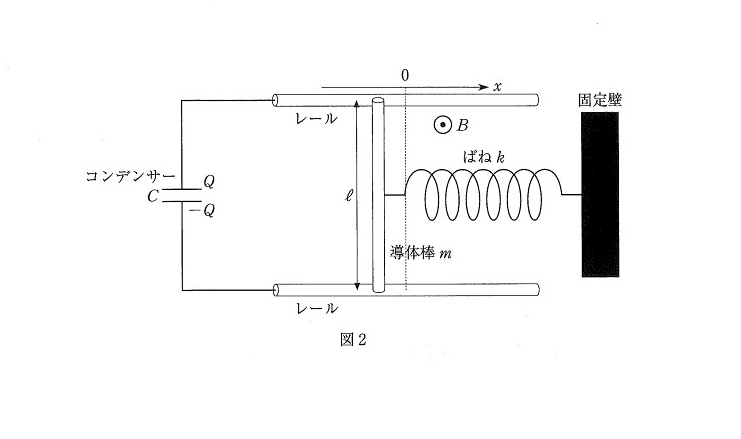

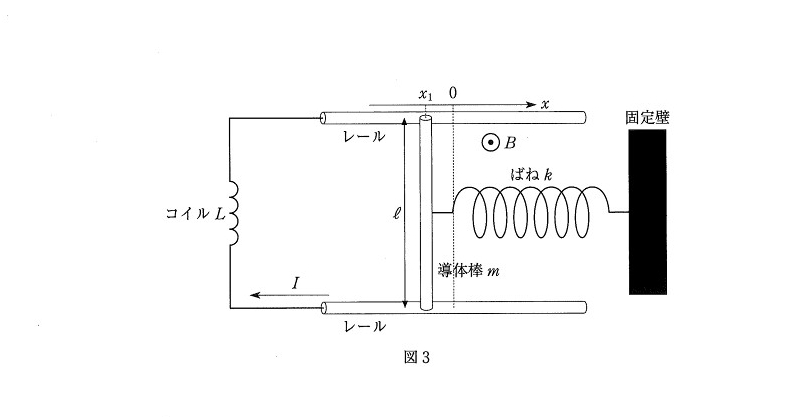
【解答】
(問1)
(a) 易

<分析>
導体棒固定なので、誘導起電力は0です。よって、オームの法則より簡単にI₀は出ます。また、F₀=IBℓの公式は大丈夫ですよね
(b) 易
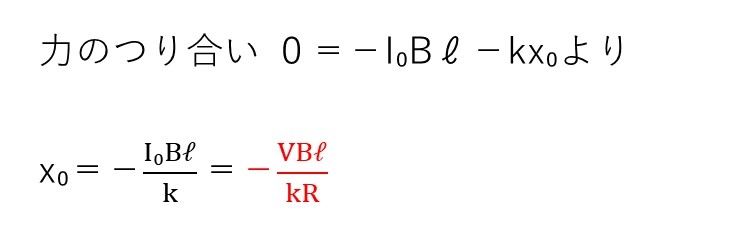
<分析>
ローレンツ力とばねの弾性力のつり合い式より、簡単に求められます。
(問2)
(a) 易〜やや易
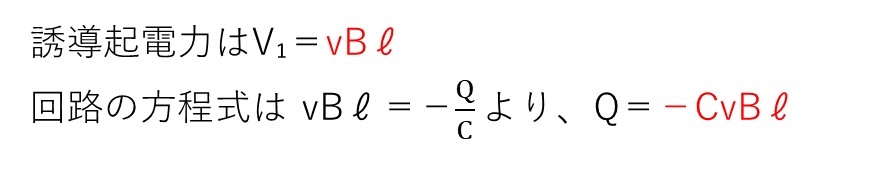
<分析>
誘導起電力の大きさ=vBLは基本知識ですね。また、コンデンサーの電位差Vは CV=Qより出せます。
(b) やや易
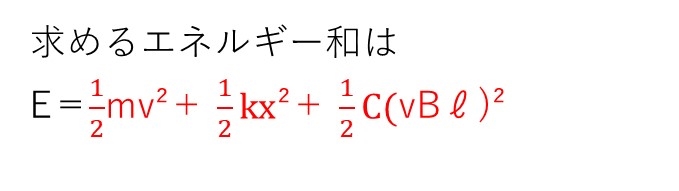
<分析>
運動エネルギーとばねの弾性力は全く問題ないでしょう。コンデンサーの静電エネルギーは前問のV₁の値を代入して出せます。
(c) 標準

<分析>
本問では運動方程式を使って解くことができません・・・このへんがいつもと違う
(b)の結果を使えと指示されているので使うのですが、河合塾の解答こんなんでいいのか?こじつけじゃないか
と思いましたが、演習慣れした受験生なら勘で答はわかるので、まあよしとしましょう
(問3)
(a) 易
L|ΔI/Δt|
<分析>
これは超基本。楽勝でしょう
(b) 易~やや易

<分析>
回路の式を立てるとおしまいです
(c) やや易
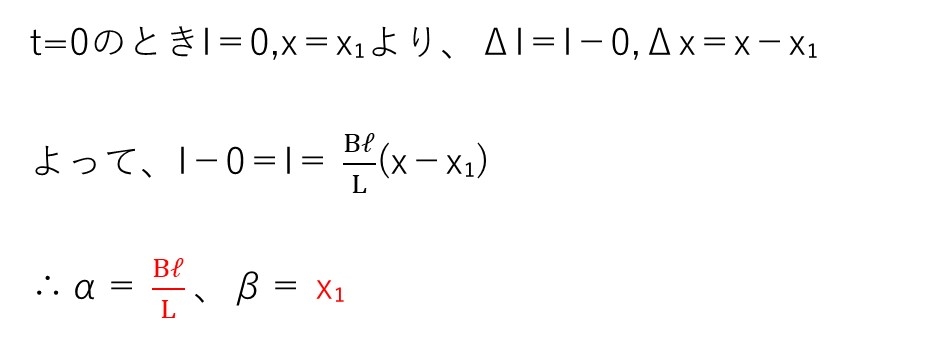
<分析>
初期条件を確認し、ΔI,Δxを変化量と捉えて解けばOK
(d) やや易~標準

<分析>
運動方程式を立てて、前問の答を代入するだけです。
(e) 標準~やや難

<分析>
(d)ができればできるのですが・・計算がやや煩雑なことと、x₁<0を見落とす可能性があることを考慮すると、まあ(d)よりは難易度高いかなと考え「標準~やや難」としました
<感想>
第1問に続いて・・・昔の東北大物理の姿はありません
問1~3までどれも誘導が丁寧で、順番に解いていくとスムーズに視界が開けるような構成になっていますしかし、問2(c)はいつもと答え方が違うので戸惑った受験生もいたでしょうし、問3後半は計算ミスで落とした受験生もいたでしょう
まあ7~8割あればいいんじゃないでしょうか
第3問


【解答】
(問1)
(a)
(ⅰ) 易~やや易
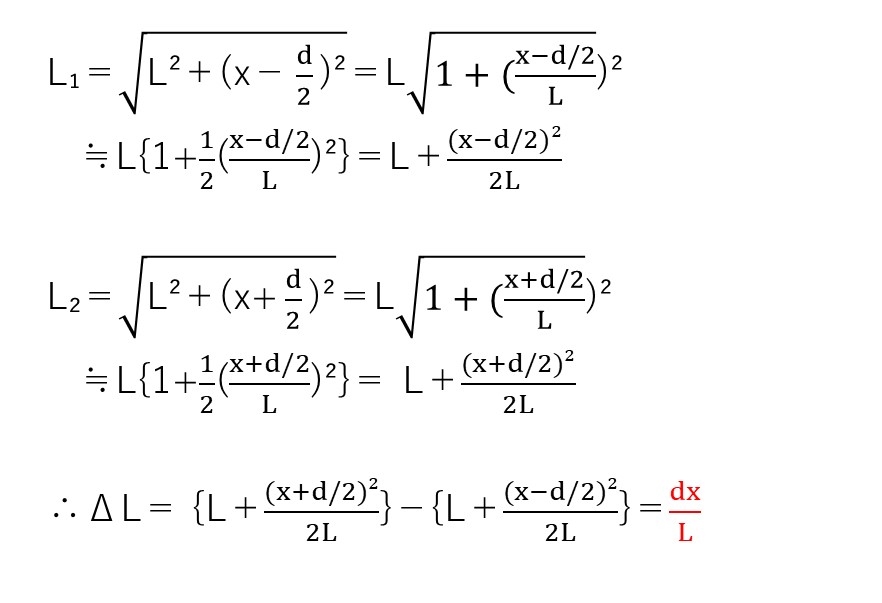
<分析>
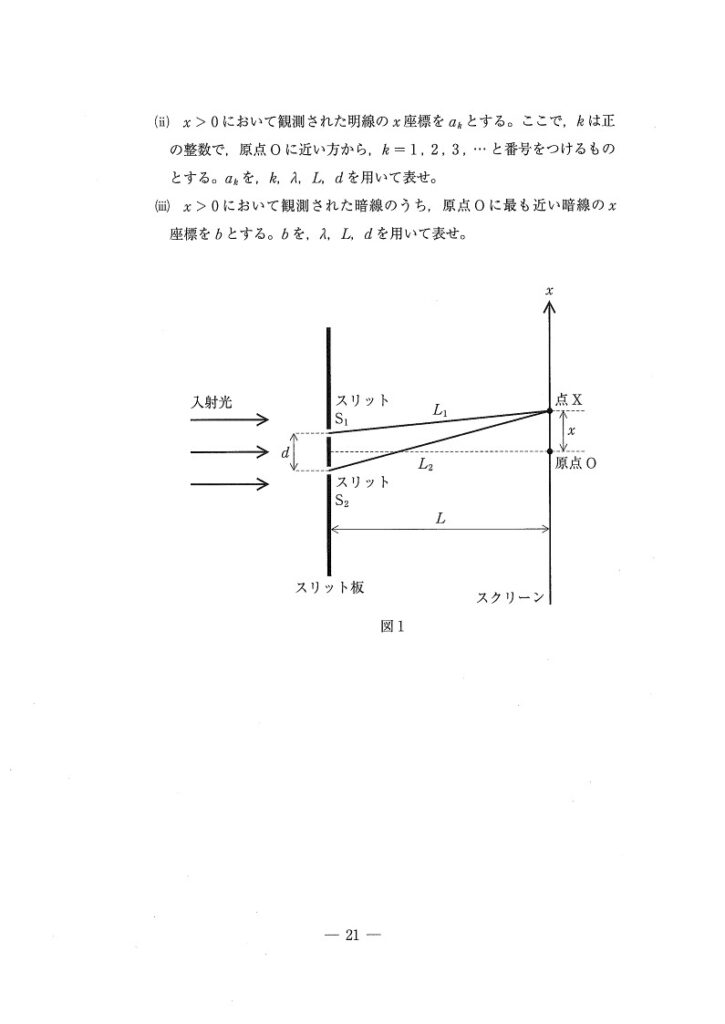
スリットを用いた干渉の問題。この手の経路差を求める問題は超頻出なので、反射的に手が動くようにしておきたいですね。
(ⅱ) やや易
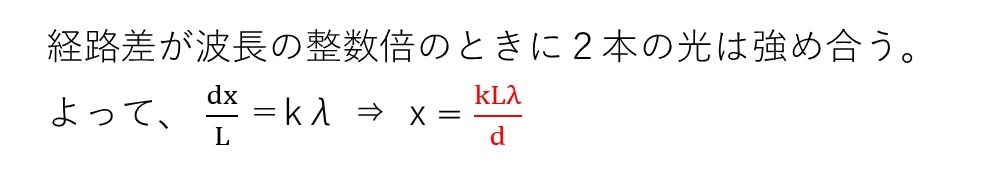
<分析>
これも超基本的。しかし、問題によっては位相がπ変わるケースもあるので、何でもかんでもmλと即決しないようにしましょう
(ⅲ) やや易

<分析>
原点で2本の光の経路差が0であることを考えると、最も近い暗線は経路差λ/2ですね
(b) やや易~標準

<分析>
光の強度が振幅の2乗に比例する旨は問題の最初に書いてあります。見落とし注意!!
(問2)
(a)
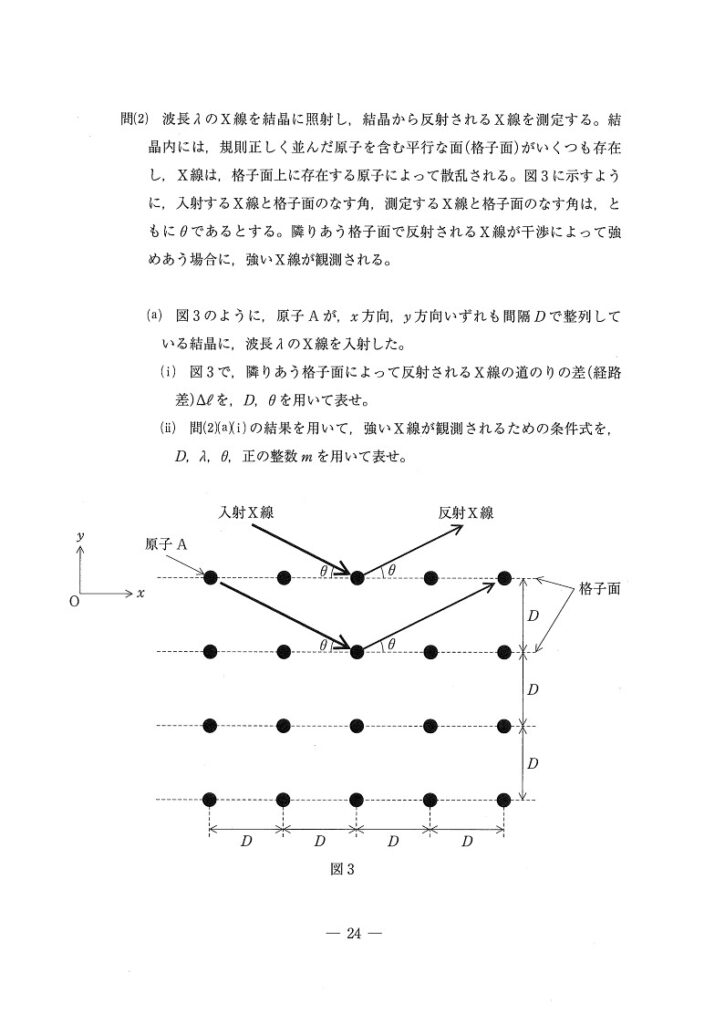
(ⅰ) 易~やや易

<分析>
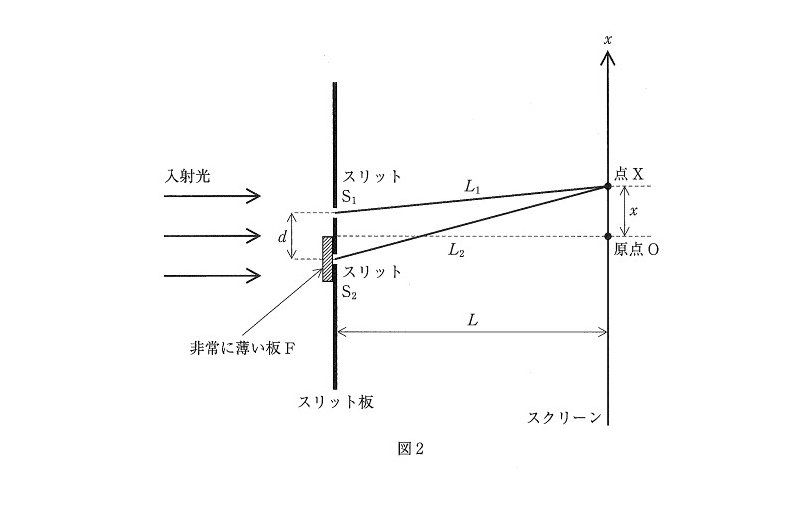
直接計算しにくい経路差は幾何的に求めることが多いです。
本問では図の赤線部が経路差になりますが、なぜ赤線部が経路差かわかりますか??
それは、同じ波面上にある光を同位相とみなしているからです
(ⅱ) 易~やや易

<分析>
これも(問1)と全く同じ考え方。
(b) 標準~やや難

<分析>
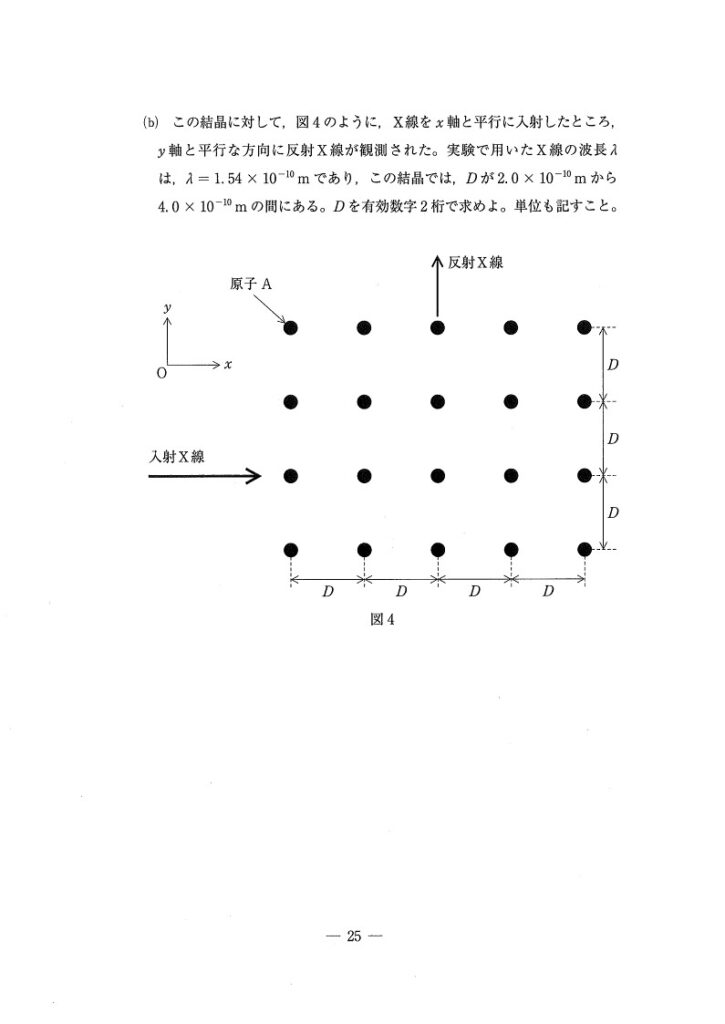
どんな現象が起きているか意味不明になった受験生もいたでしょう。なぜ反射波の向きが90度変化したのでしょうか
なぜそうなるかを考えてみましょう。
実は、図3ではあった格子面が図4では書かれていません!これが何を意味するか?・・・自分で格子面を特定してね!ということです
格子面がわかれば、あとは(a)の要領で解けばOK。なお、距離はD/√2でθ=45°になります。

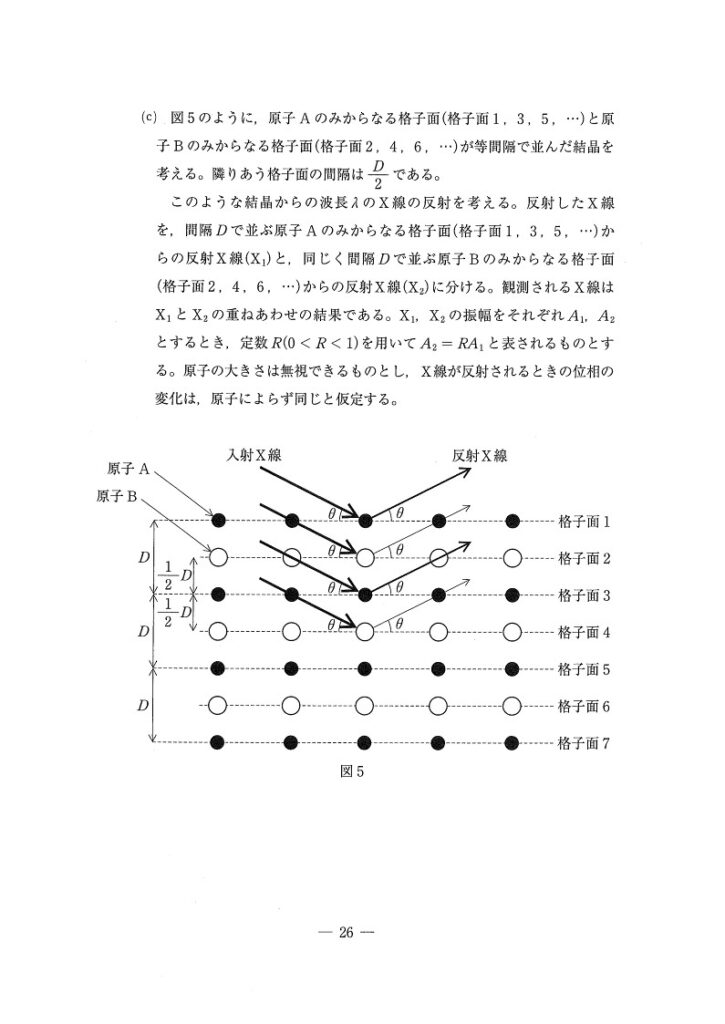
(c)
(ⅰ) 標準

<分析>
問題の意図がつかみにくいのですが、X₁どうし,X₂どうしが強め合う条件を求めてほしいようですね。
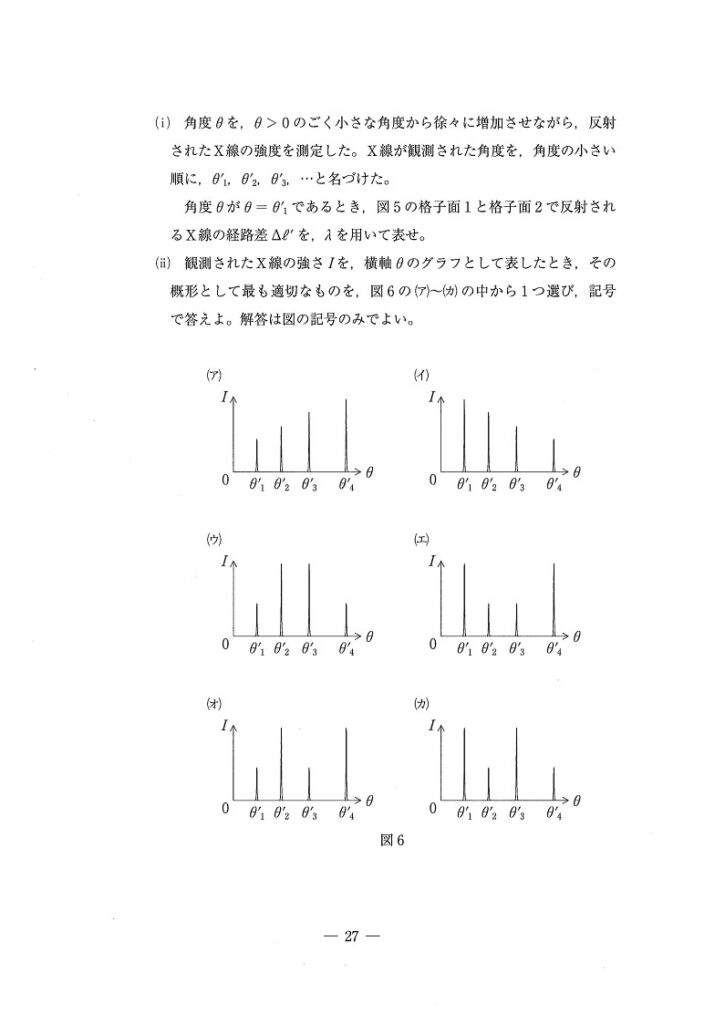
(ⅱ) 標準
オ
<分析>
θ=θ₁’のときΔℓ₁’=λ/2、θ=θ₂’のときΔℓ₂’=λ・・・のように順々に考えていくと、X₁とX₂は弱め合う⇒強め合う⇒弱め合う・・のように変化します。
よって、光の強度も弱⇒強⇒弱⇒・・・と変化することがわかるので、答は(オ)です。
<感想>
問1はスリットを用いた干渉の問題で、超典型的。毎年,毎回のように旧帝大のどこかで出ているので、これは即答で答えられるようにしましょう。
問2は結晶格子の反射。(b)が思考力を問う良問です。誘導に従う系の問題ではなく自分で解法を見出す問題で、頭を鍛えるのに適しています。(c)は問1(b)の応用。X₁とX₂の経路差を考えれば周期的に変化することがわかるでしょう
なお、原子物理の要素は全く含まれていませんでした
第1,2問に比べると少しは歯応えがありましたね。問2(b)や問3(b)はなかなかの良問ではないでしょうか
総括
北大よりは歯応えがありましたが、やはり約20年前の重量級の東北大物理のこと考えると全然軽いです
とはいえ、記述式で分量も多いので、処理能力の有無でそれなりに差は付くかと
明らかにこれはムズイ!という問題は皆無でしたが、敢えてどれが取りにくいかと言うと、第3(問2-b)ですかね~
合格点は
非医:55~60%
医:70~75%
程度でしょうか。
以上で解説を終わります。
最後に、再度公式LINEの紹介をします。
公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信する公式LINEはこちら
登録していただいた方には、無料プレゼント贈呈



















