
受験生の皆さん、こんにちは。
東大合格ビジネスマンのワタシですm(_ _)m
私のブログでは
① 入試問題の解答・解説
② 受験合格に必要なマインド
③ 3大基礎力重視の裏ワザ勉強法
について、様々な情報を発信しております📢
私の公式LINEでは無料相談を随時受け付けております。公立中出身から東大理Ⅲ,京大医学部のA判定に辿り着いた私が、大手予備校や受験秀才が言わない情報を存分に発信します。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってください✊
私も苦手科目は先生に頼りました。
また、LINE登録していただいた方には、無料プレゼント(1年で偏差値70出す画期的勉強法)を贈呈します🎁
無料相談もどしどし受け付けております✊
【⬇️公式LINE登録はこちら⬇️】

2021年入試、旧帝大の第2弾は
「東北大学」です。
当ブログの解説記事は、長期的な目線で成績を飛躍的に伸ばし、継続性・応用性のあるスキルを身に付けていただく記事です。
読者が必死に3年間努力すれば
東大(理三以外)・京大(医以外)・九大医
レベルに80%以上の確率で合格できる
ことを目的に作成しています
市販の問題集のように、解法を丁寧に示すだけではありません!
多角的なアプローチで、適所で関連事項や模範解答ではない解説を投入し、必要以上に問題を解きほぐしています✊
① 各問の難易度
② 他分野や一般常識との関連事項
③ 問題の躓きポイント
④ 極力曖昧な表現をしない説明
を示しています。
イマイチ成績が突き抜けられない受験生に貴重な情報が提供できればと思いますm(_ _)m
東北大物理の特徴
東北大学の理科は2科目で制限時間は150分です。そのうち、物理は全3問。
約15年前までは東北大の物理は鬼畜な問題を出すと恐れられていましたが…最近は穏やかな出題が続いている印象です。
2021年の北大や九大よりは1段階難しい印象。
深く理解するには
全統記述模試で偏差値58~62程度
は欲しいですね🧐
全統記述模試の難易度や受験者レベルについては、各自で確認されてくださいm(__)m
第1問

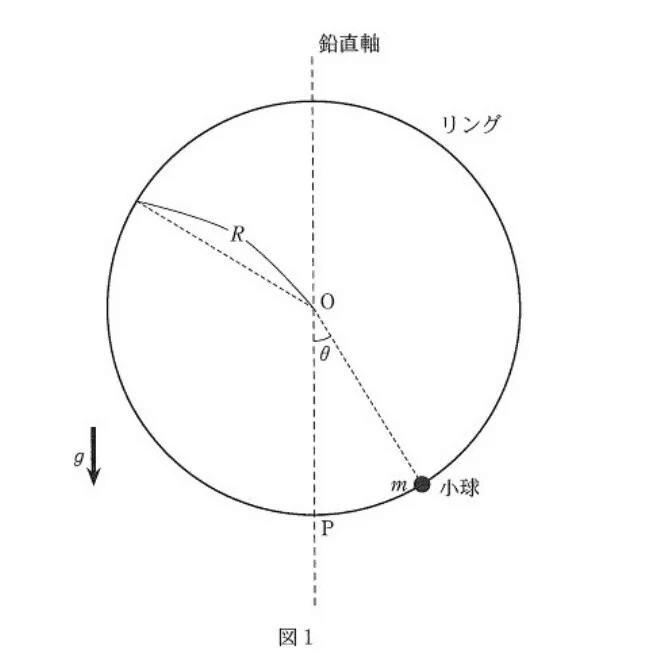

【解答】
(問1)
(a) 易

<分析>
高さの差が出れば楽勝な問題です。
(b) 易

<分析>
ただのエネルギー保存則の問題です。
(c) やや易

<分析>
何となく、v>0としてたまたま解けた受験生もいたでしょう😅
しかし、糸と繋いであったり、レール上を動く場合は、張力や垂直抗力を考えないといけないので、その場合はv₁=2√gRではないですよ!
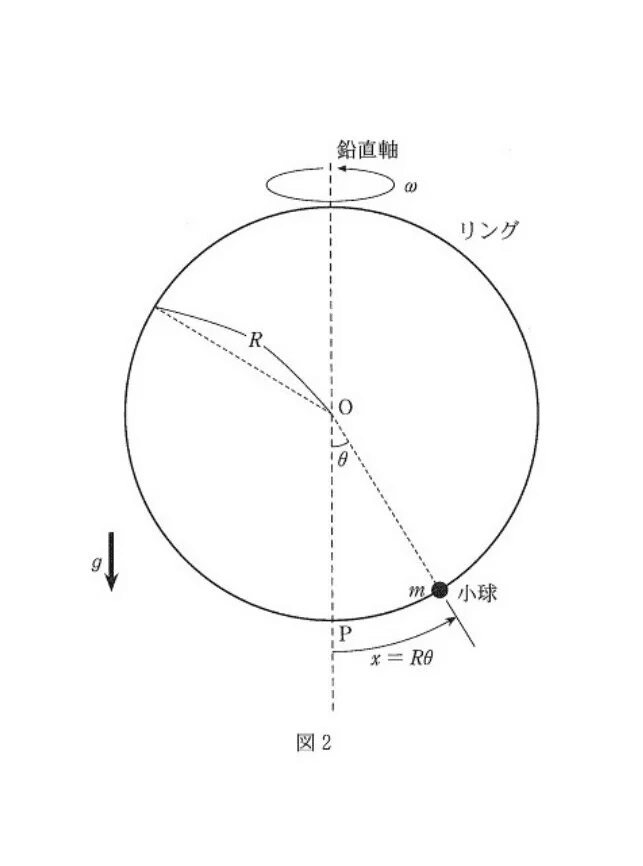
(問2)
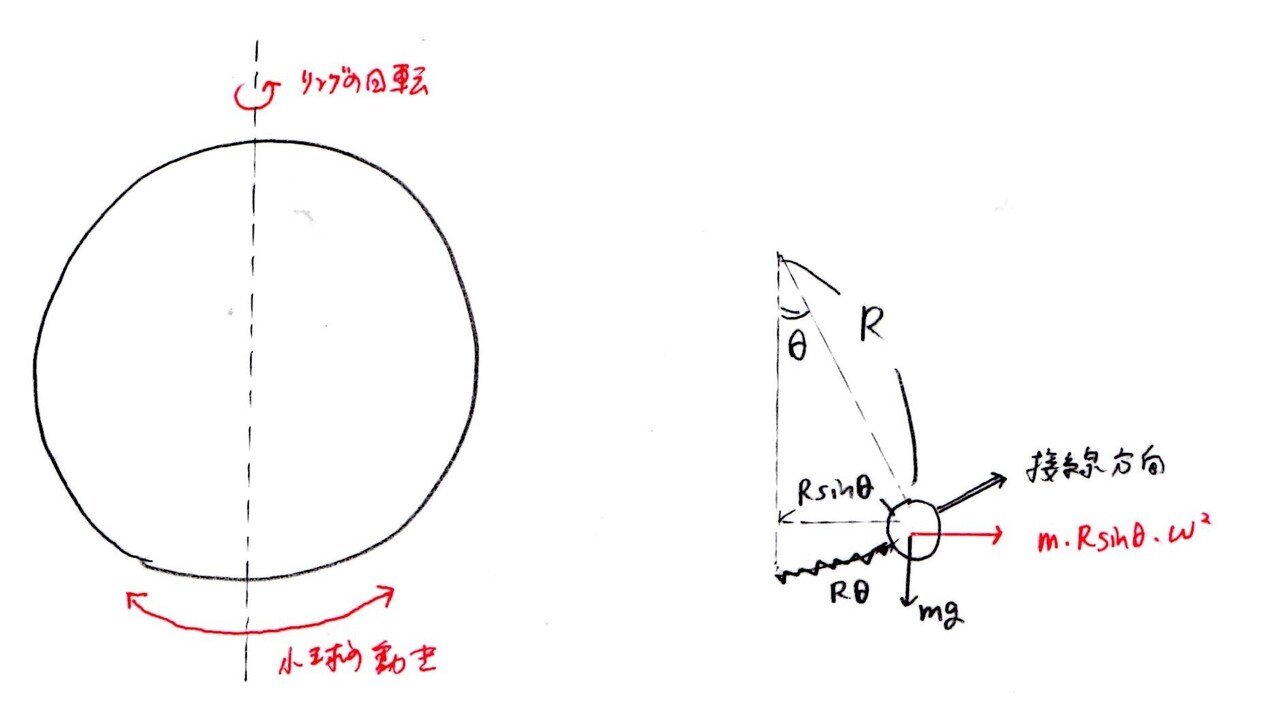
小球とリングの運動は同一平面上にないので、そのままだと考えにくい💦
よって、リング上の人から見た小球の動きを考える。
つまり、小球に遠心力を追加して考える。
(a) やや易〜標準
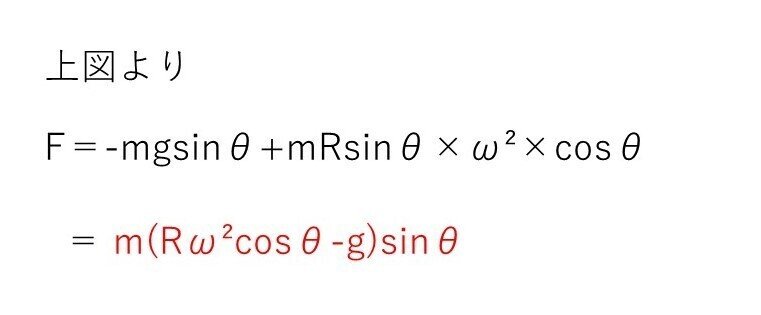
<分析>
ここは、慣性力を意識できたかが全てでした☝️
何で?小球が振り子運動をするのは、リング上の人から見たときの話だからですよ☝
(b) 標準

<分析>
θを「変位」と捉えるのに苦戦した受験生がいたと思います。
数学Ⅲの知識なんですが、これが物理や化学になると出てこない人、結構いるんですよ💦
(c) 標準

<分析>
大丈夫かとは思いますが、リングの角速度ωと求める角振動数をゴッチャにしてはいけませんよ💨
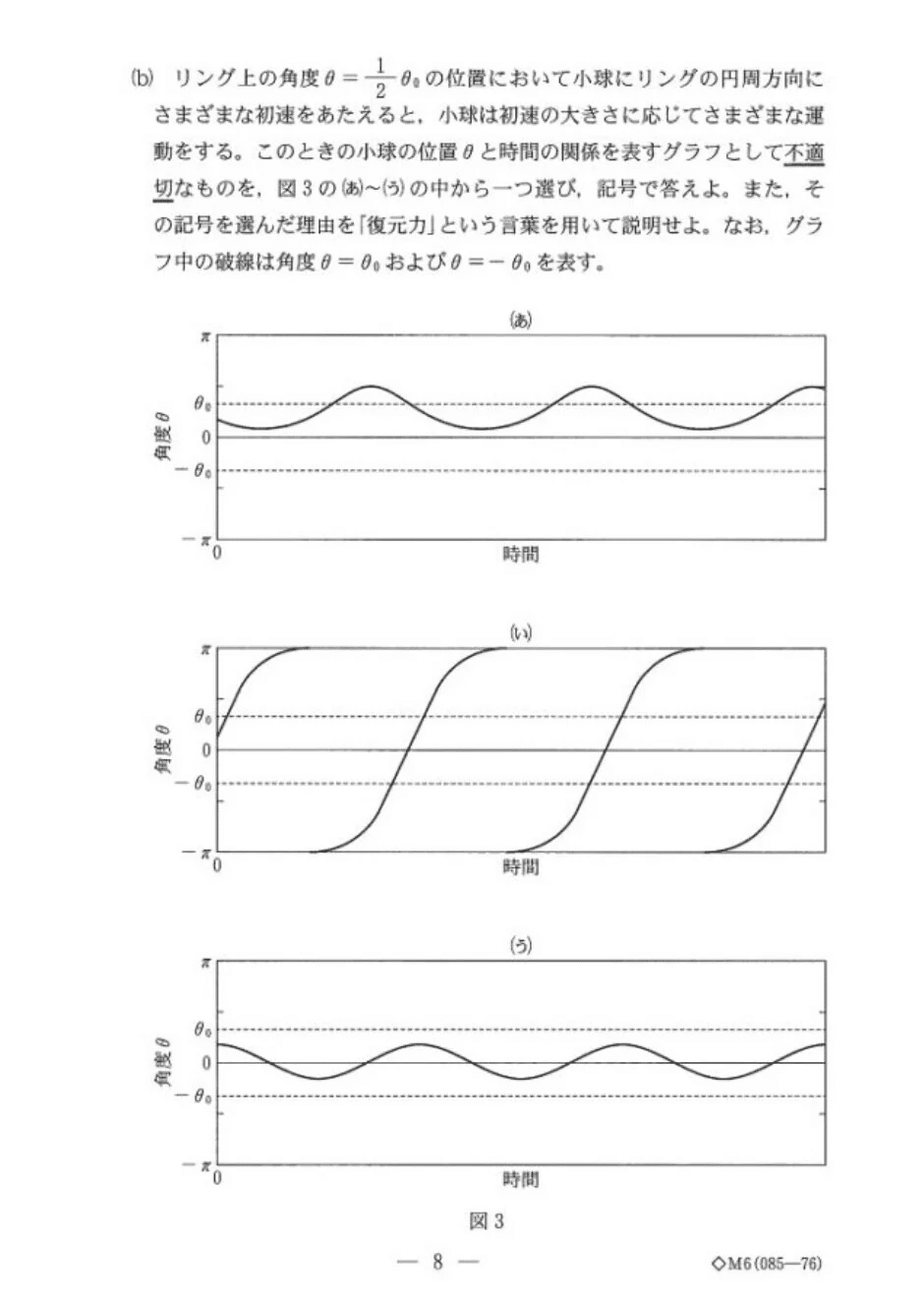
(問3)
問2(b)(c)と違って、微小角ではないことに注意しましょう!
(a) やや易~標準
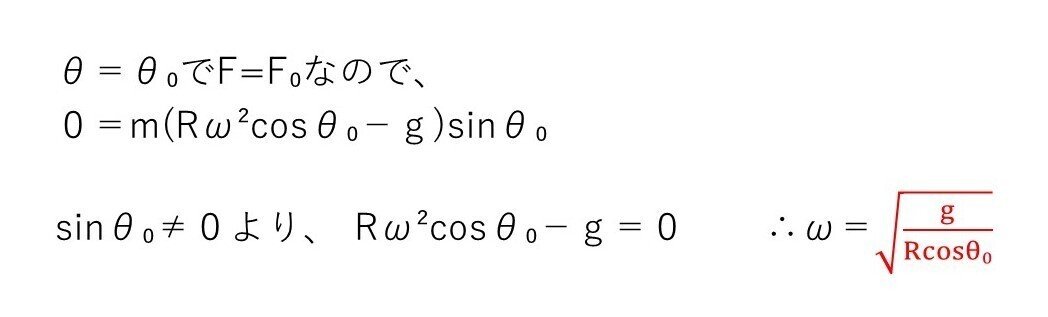
<分析>
これは問2(1)が出ていれば楽勝でしょう。
(b) 標準
う
<分析>
ω>ω₀のとき、問2(b)よりθ=0が単振動の中心にならないのは明らか。
ここでは、θ=θ₀を中心に単振動することから、(う)は不適。
(あ)はリングを1回転するケース、(い)はリングの最高点にはいかずθ=θ₀を中心に単振動するケースでしょう(もちろんリング上の人から見て👀)。
<感想>
円運動of円運動とでも言うべき、興味深い問題です👀
ここでの重要ポイントは「2物体の運動=慣性力を意識」。回転するリングの観測者から小球の動きを見る際に、慣性力(遠心力)を意識できるかで大差がつくと思われます。
第2問



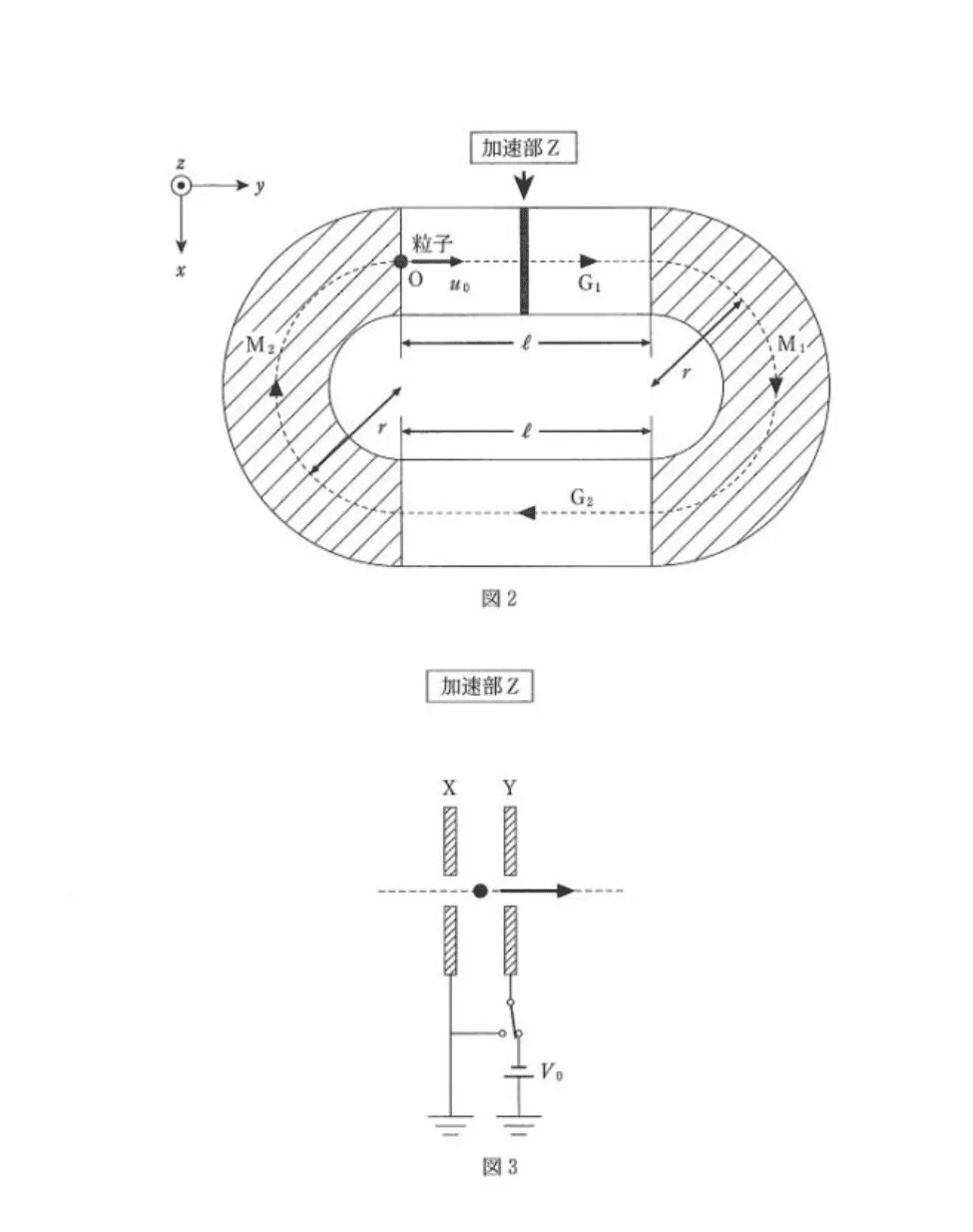

【解答】
(問1)
(a) 易
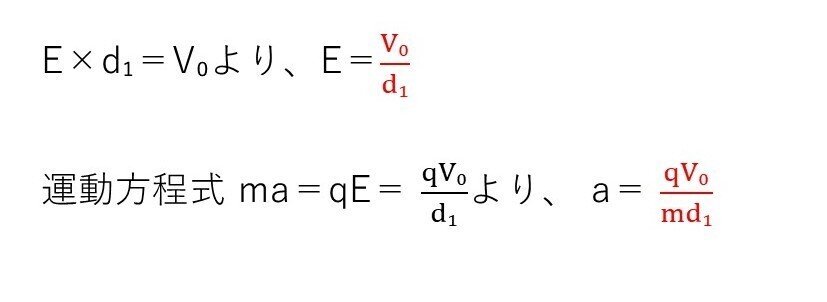
<分析>
典型問題ですね。(電位差)=(電場)×(距離)を使い、運動方程式を立てれば終わりです。
(b) 易~やや易
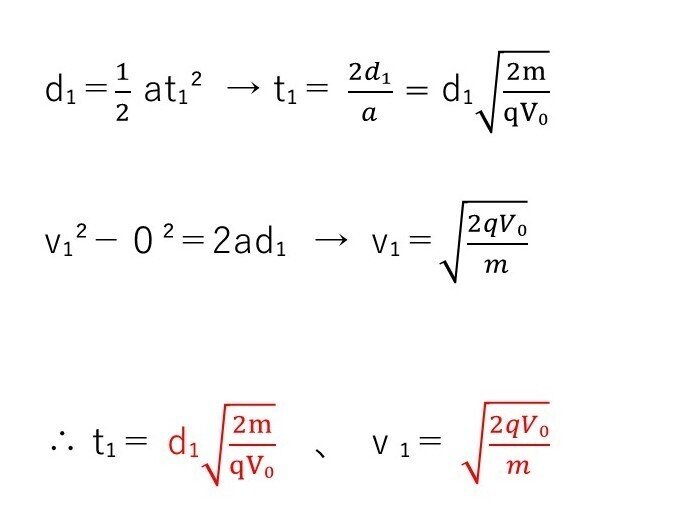
<分析>
距離,速度,加速度間で成り立つ有名公式3つ・・ありましたよね?
それを使うだけの問題です。
(c) やや易
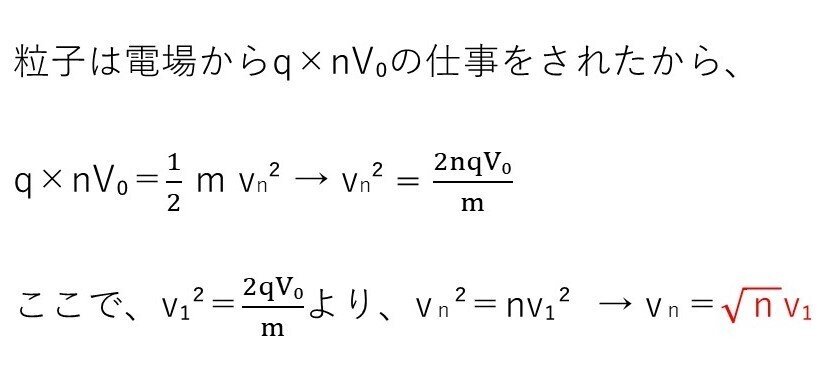
<分析>
電位差V₀の極板をn回通るので、された仕事はnqV₀です。
あとは、その仕事が粒子の運動エネルギーになったと考えればOKです☝
(d) 標準

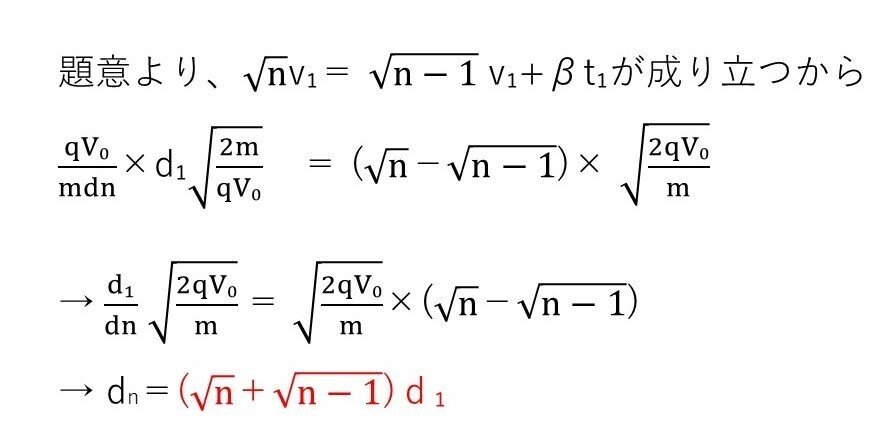
<分析>
(c)の結果を利用します。加速度をdnで表せば、速度と加速度の式からdnを求めることができます!
(問2)
(a) 易
+z方向
<分析>
領域M₁に入った直後の粒子が時計回りに円運動するので、フレミング左手の法則を使って、磁場がどの向きのときにローレンツ力が円の中心方向を向くかを調べます。
まあ2択なんで、50%の確率で当たるんですが(笑)
(b) 標準

<分析>
円運動の加速度の向きは進行方向と垂直です!
答自体は、「力=質量×加速度」を考えると何となくわかるとは思いますが💦
(c) 標準~やや難

<分析>
1周する間の速さは一定なので、その速さuNがわかるとOKでしょう。(b)の関係式を利用すると出ます。
(d) 標準~やや難
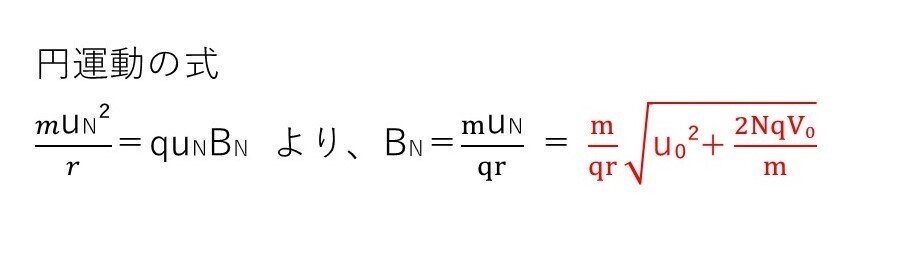
<分析>
問題自体は簡単。しかし、(c)でuNを出す必要があるため、難易度も(c)に準じます。
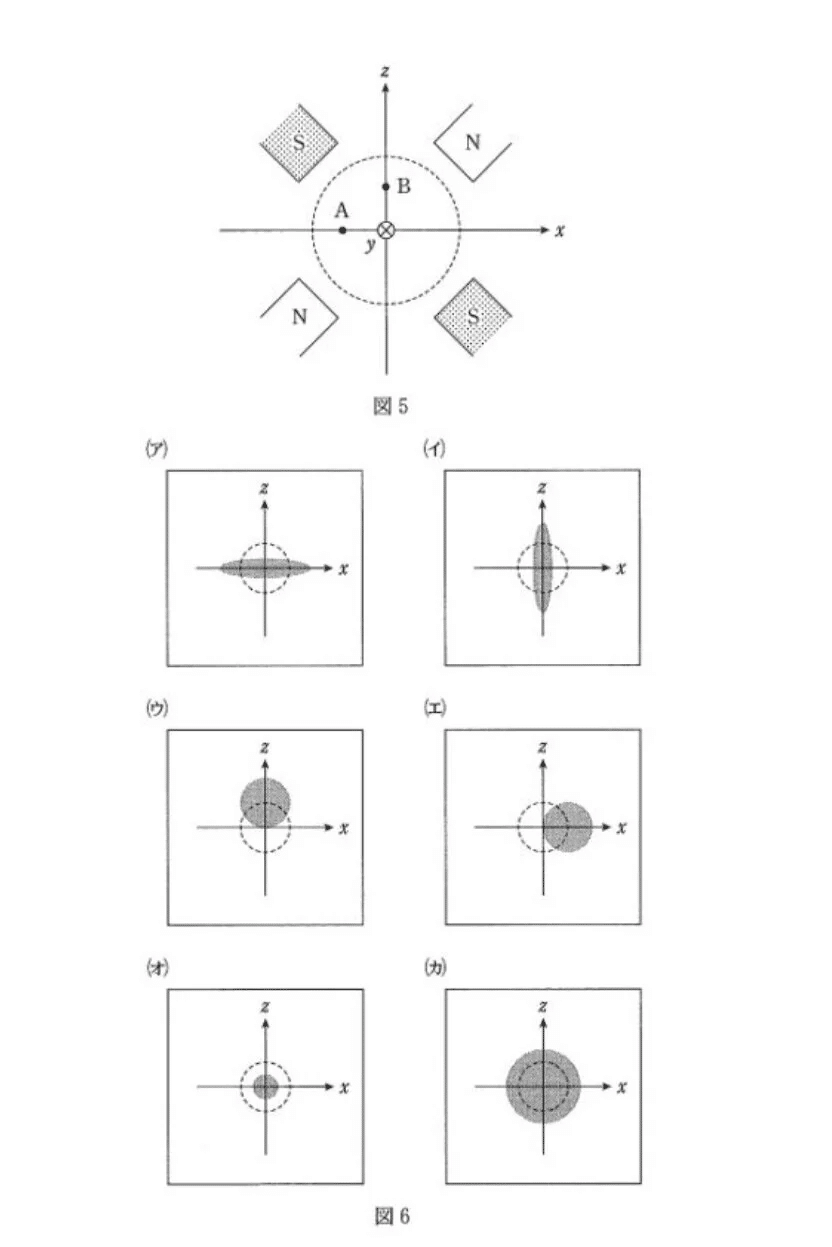
(問3)
(a)(b) やや難
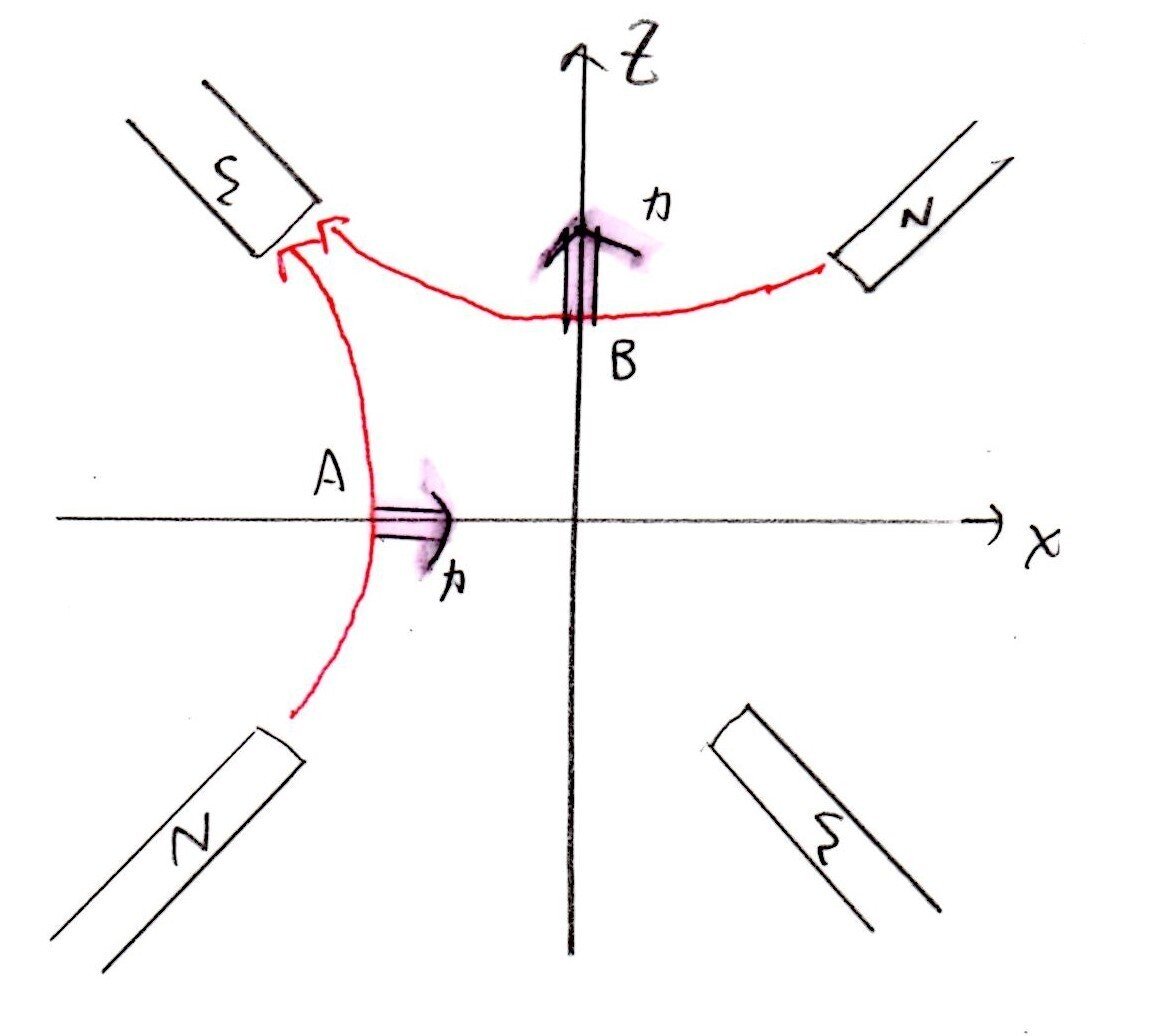
<分析>
新傾向問題で面食らった受験生も多かったでしょう。
しかし、考え方自体は電場と同様で、力もクーロン力からローレンツ力になっただけです。
磁力線がN→S極へ向かうことを理解していれば、磁場の向きは赤線のようになります。また、力の向きはフレミング左手の法則より、ピンクマーカーの向きになります。
(c) やや難
イ
<分析>
(b)の力の向きを考える。「点Aに働く力によりx軸方向には狭まり、点Bに働く力によりz軸方向には広がる」と考えられる。
<感想>
第2問はよくある荷電粒子の電場(or磁場)内での運動です。問1,2は、緻密な調査と漸化式を解く点で少し手間取りますが、状況を追って立式すれば、さほど難しくないです。
目玉は新傾向問題っぽい問3でしょう👀
(a)をどう攻略するか?(c)は前問の結果を踏まえてどう考えるか?
が着眼点でした。
問3は磁力線を電気力線と同じ要領で考えられたかがカギでしたね🔑
第3問



【解答】
(問1)
固定端反射 → 位相がπずれる!
(a) 易
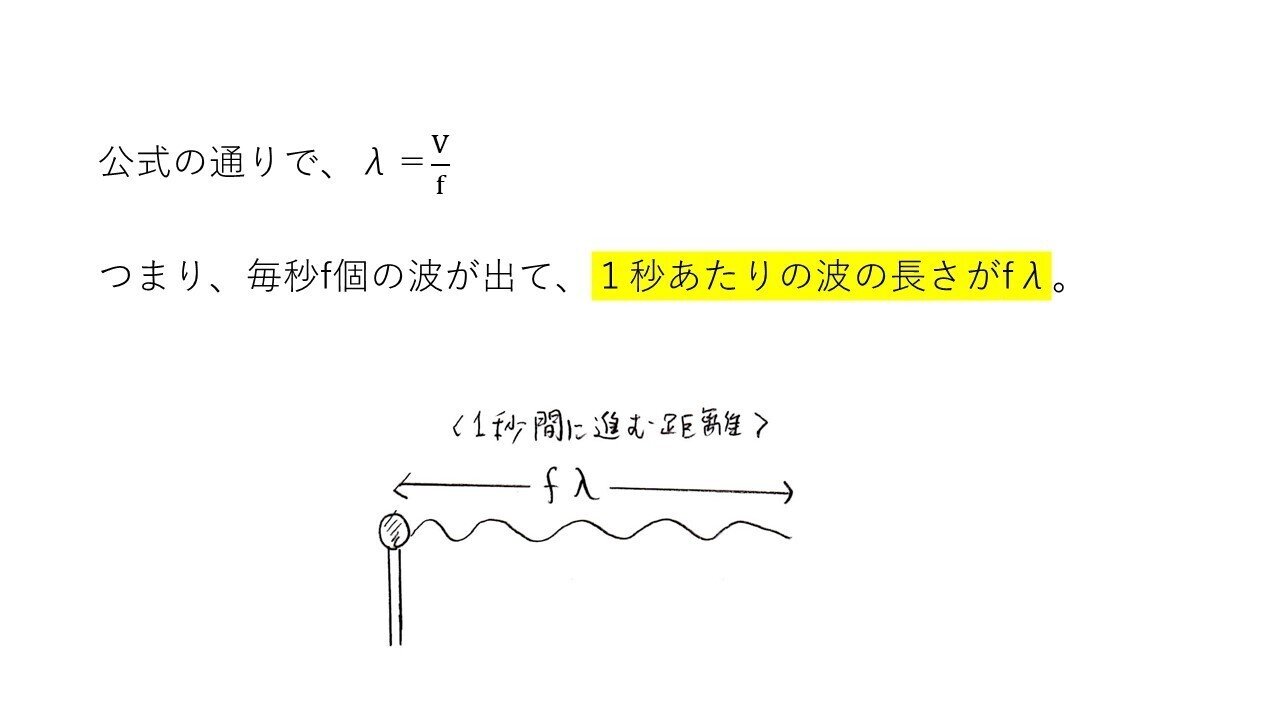
(b),(c) 標準


<分析>
F=-FRの条件より、sinの中身を=で結んでa=2dを出しても構いませんが、本当は(b)の段階で三角関数の積和の公式を用いてa=2dを出すのが筋だと思います。
(d) 標準

<分析>
(c)で出た振幅が常に0となるxが0<x<dに存在すればよいので、2πf(d-x)/Vのとりうる範囲が0~2πfd/Vであることより2πfd/V >πであればOKです。
(問2)
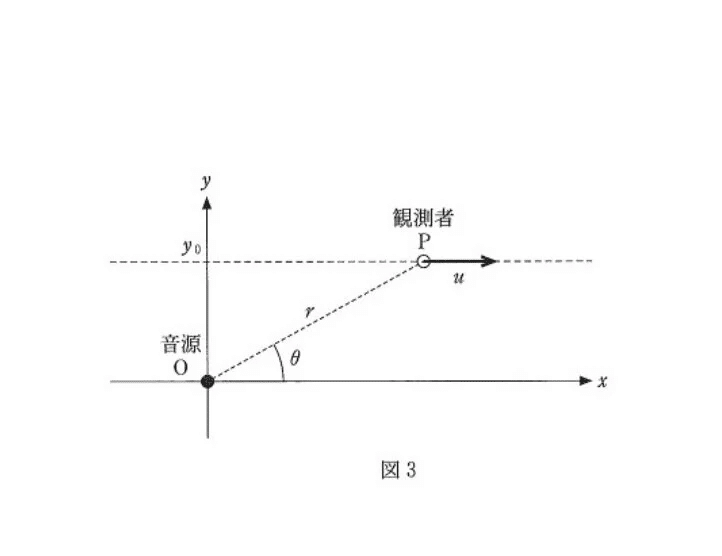
(a) 易
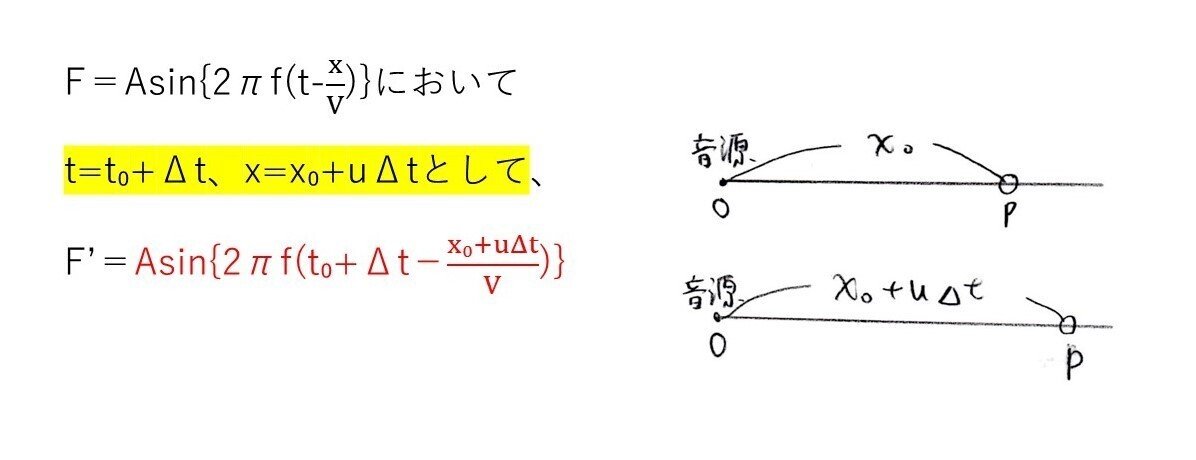
x = x₀+uΔt
<分析>
実質、小学5年レベルの問題です。
(b) やや易
(c) 標準

<分析>
観測者Pからすると、x=x₀からx=x₀+uΔtに至るまでに1周期分の音を聞いたと考ええれて、周期Tを求めればOKです。すると、T=1/f’より振動数f’も出ます。
(問3)
(a) やや易

ここで、cosθ=x₀/r₀ よりOP=r₀+uΔtcosθ
<分析>
計算処理は多少面倒ですが、ただの三平方の定理と近似式です。
(b) やや易
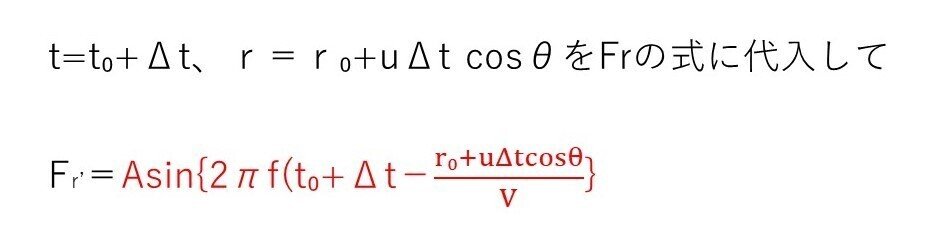
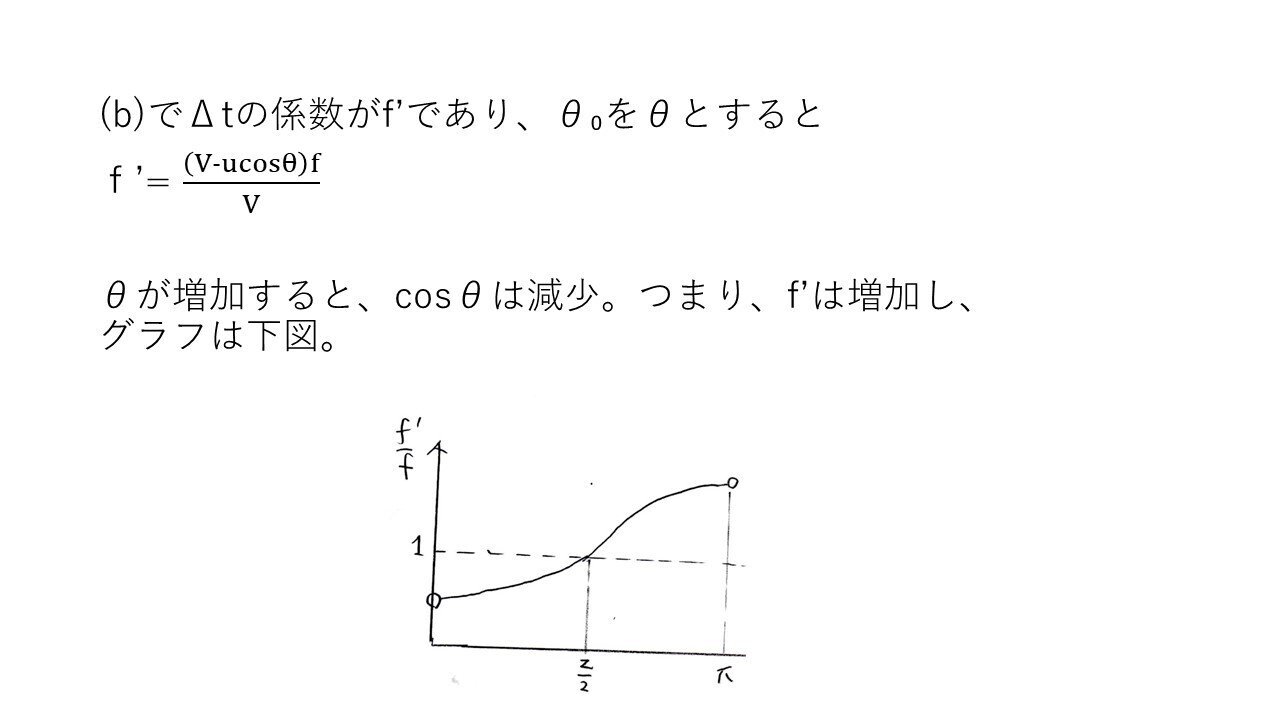
(c) 標準
<分析>
(b)で出たFr’をAsin2πf'(t-○)の形に変形し、振動数f’を出してから考察する問題でした。
あとは、0<θ<πでcosθが単調減少であることから考えればOK。
<感想>
観測者が聞く振動数を求める問題。答を出すだけなら簡単だけど、波の式から工夫して求めるとなるとやや難しいですね~😥
総括
第1問は慣性力に免疫があるか、
第2問は計算処理と問3の新傾向問題。
第3問はドップラー効果の結果を波の式を変形することで出せるかを試す問題でした。20年前のハイレベルな出題と比べると全然マシですが、所々に手をつけ辛い問題は散在しています。
合格点は
非医:55~60%
医:70~75%
でしょうか。
特に、第3問は波の式を上手に扱えるか否かで得点差が開いたと思われます。
医志望は第3問での崩壊を回避したいところ
ですね。
最後に、再度公式ラインの紹介をします。
私の公式LINEでは、無料相談を随時受け付けております。
成績が低迷しているのに1人で悩むのは時間の無駄ですから、受験のプロを頼ってみてください✊
【⬇️公式LINE登録はこちら⬇️】






